基于HSPICE温度对长条形磁通门输出的影响*

侯晓伟，刘诗斌，李菊萍，郭 博

(西北工业大学电子信息学院，西安710072)

磁通门传感器是利用高导磁铁芯在饱和交变激励下选通调制铁芯中的直流磁场分量，并将直流磁场转变为交流电压输出而进行测量的一种磁测量传感器，它主要用于测量微弱磁场(如地磁场)。磁通门传感器具有分辨率高、测量范围宽、噪音低等特点，尤其是具有适用温度范围广的特点，是综合性能优良的磁测量传感器，得到广泛的研究。磁通门已广泛应用于地质探矿、车辆控制、潜艇、航空航天等领域[1]。

由于磁通门传感器固有的非线性性质，其输出的解析表达式难以用确切的公式表征。影响磁通门传感器输出性能的因素主要有:温度、频率、电压激励(或电流激励)、压力等，它们在不同程度上影响着输出的性能。文献[2]提出了基于Jiles-Atherton theory(简称JA理论)，建立了基于JA理论与温度有关的磁滞模型。通过与温度有关的磁滞参数将热效应添加到该模型当中，新增加了临界参数、居里温度等参数，并通过钴铁氧体材料的实测参数，验证了新模型的有效性，仿真结果与分析结果吻合的很好。本文在文献[2]的基础上，采用新提出的与温度有关的JA模型，首次提出利用Hspice进行建模，通过大量的仿真数据分析，从理论的角度阐释了温度对磁通门传感器输出的影响，该工作对磁通门的影响因素进行了有效地补充和完善。

1 磁通门铁芯的描述

磁性材料的非线性和磁滞特性对传感器性能具有重要的影响，因此，在磁通门的数值模拟计算中，需要采用合适的理论模型来描述传感器铁芯。

JA 模型:David C Jiles等人[3]提出的 Jiles-Atherton模型是描述非线性磁芯特性的主要物理模型。该模型通过确定几个与材料相关的参数，求解一个微分方程后就可以获得该材料中磁通量变化与磁场的变化。而由于JA模型所采用的数学方法非常适合用来进行数值计算，因此在磁场等非线性电路模拟领域得到广泛的应用。

JA模型将材料的磁化过程分为两部分:可逆磁化和不可逆磁化，其中发生不可逆磁化时能量将被损耗。总的磁化过程是上述两种磁化的综合反应。总公式为:

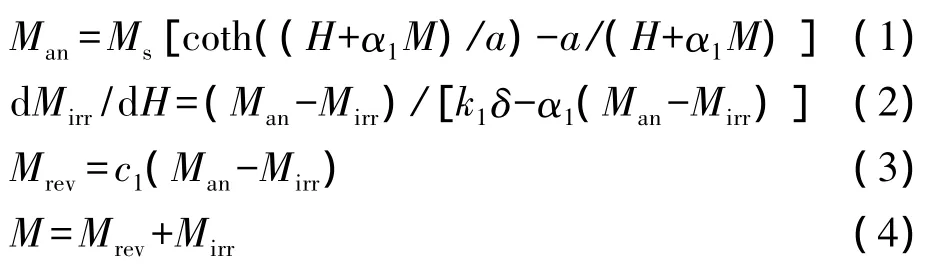
式中Man为无磁滞磁化强度，Mrev为可逆磁化强度，Mirr不可逆磁化强度，H为磁场强度。δ为方向参数，当 dH/dt＞0 时取+1，当 dH/dt＜0 时取－1。5 个模型参数分别为无磁滞磁化强度形状参数a(A·m－1)，磁滞损失参数 k1(A·m－1)，平均场系数 α1，可逆磁化强度系数c1和饱和磁化强度Ms。为了有效建立JA模型，需要提取JA参数，所需的一组参数为:饱和磁化强度、饱和磁场强度、初始磁化率、初始无磁滞磁化率、矫顽力、矫顽力对应的磁化率、剩余磁化强度、剩磁处对应的磁化率[3]。

以上4组方程并不适合在HSPICE中建立宏模型，这是由于在有效磁场较大时，式(1)为两个奇异函数之差，收敛性质很差[4]。

JA模型能充分的反映磁芯磁化过程中的磁滞饱和现象，因此在磁开关、变压器等磁芯应用领域其模拟结果有较大的可信度。HSPICE磁芯元件库Magnetic.Lib元件库中，软件提供了几百种商业磁芯的参数配置，而对于不知道型号的磁芯，只要能获得其一定频率下的磁滞回线，就可以比照曲线调整参数。当模拟出的磁滞回线和测量曲线一致后，就可以对该频率下含磁芯的电路进行准确度模拟[5]。

JA模型虽然在描述磁滞饱和方面得到广泛应用，但是它在磁芯特性模拟方面有其本身缺陷，比较明显的是该模型未考虑频率和温度的因素。例如:当激励频率增加时，由于磁芯损耗增大，磁滞回线会变宽;当温度超过一定量值(居里温度)时，磁性材料由铁磁性转变为顺磁性，极大地改变了磁性材料的性质。

产生上述问题的原因是:由于JA模型对磁特性的模拟是由各个参数决定的，而参数需要在电路模拟前设定好，因此，在模拟过程中一些时变的量对磁芯特性的影响是JA模型所不能反映的，例如温度和激励波频率的变化。在许多磁芯应用场合，如脉冲变压器、感应加速器等，其工作的频率(或脉宽)是需要常常改变的，而对一些需连续工作的感应腔或变压器而言，则其工作温度是在一定范围内变化的[6－8]。

2 基于温度的JA模型

针对 JA模型的这些不足，A Raghunathan等人[2]对JA模型进行了改进，添加了随温度变化的参数。该模型可以有效的反映温度对磁性材料的影响。该模型主要由以下几部分组成:

通过以下4个式(5)～式(8)的4个与温度有关的磁滞参数:自发磁化强度Ms、磁畴耦合系数α、钉住系数k、可逆磁化强度系数c，将热效应导入到JA模型中。

(1)自发磁化强度Ms

与温度有关的自发磁化强度Ms可以用电磁学中的Weiss理论来表示成:

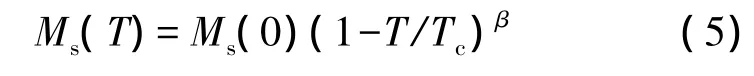
其中Ms(0)是在热力学温度为0 K时的自发磁化强度，Tc是居里温度，β是与材料有关的临界指数，由平均场理论[9]得到。

(2)钉住系数

在软磁材料当中，钉住系数约等于矫顽力，即k=Hc。由于铁磁材料中矫顽力场的指数式衰减，根据式(6)，磁畴壁钉住系数k随温度呈指数变化。其中k(0)是钉住系数在热力学温度为0 K时的值，β是临界系数。

(3)磁畴密度

尽管磁畴密度表示了关于温度的函数，但是它对温度仅有很小的变化，可以忽略不计。因此，在此模型中，k可以视为常数。

(4)磁畴耦合

磁畴耦合α，是表示磁畴间磁相互作用强度的物理量，在各向同性材料中表示为:

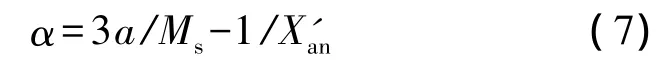
在无磁滞磁导率X'an不断增大时，上式第二项对磁畴耦合的作用几乎可以忽略不计，因此，把简化后的式(5)代入式(7)可得:

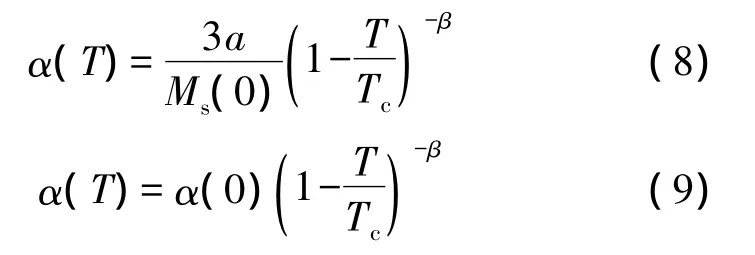
其中，α(0)是磁畴耦合系数在0 K时的值，β是临界系数。

(5)可逆磁化强度系数

可逆磁化强度c的获得与磁畴耦合系数的方法相似，对于各向同性材料，表示为:

假定初始磁化率X'in为常数，把式(5)代入式(10)得到:

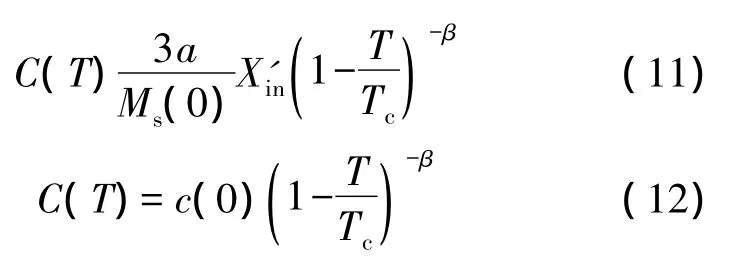
其中c(0)是可逆磁化强度系数在0K时的值，β是临界系数。

决定磁化强度过程的 Ms(0)、K(0)、α(0)、c(0)、a等磁滞参数，可以通过在0 K时的初始磁导率X'in、无磁滞磁导率X'an、矫顽力Hc、剩磁Mr等磁场参数来确定。确定步骤在文献[10]中有详细描述，能满足建模要求。测定的自发磁导率作为温度的函数，通过式(5)用来估计临界指数β和居里温度Tc。

这个过程将确定所需的所有参数，以描述磁滞在任何温度下直到居里点的行为。

3 磁通门与基于温度参数的JA模型的结合

对于钴基非晶铁芯材料，由测得的磁滞回线[3]可得常温下(25℃)的磁滞参数为:Ms=3.8e5，

α=1.462 3e－005，a=3.651 3，k=4.245 6，c=0.3405。换算为热力学温度，并计算得在0K下的初始磁滞参数为:Ms(0)=5.192 7e5，k(0)=63.747 7，α(0)=1.070 2e－005，c(0)=0.249 2，a=3.651 3。其中测得的临界系数 β 约为0.4，则式(5)、(6)、(9)、(12)可表示为:

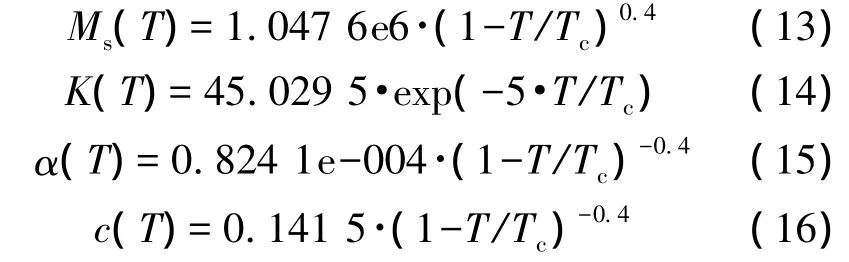
图1、图2和图3，常温表示25℃，横轴表示的是被测磁场Hx(单位:A/m)，纵轴表示的是磁通门二次谐波点的幅值V2(单位:V)，它的归一化输出电压为:Vout=V2fNA，其中f为激励频率，N为线圈匝数，A为铁芯面积。

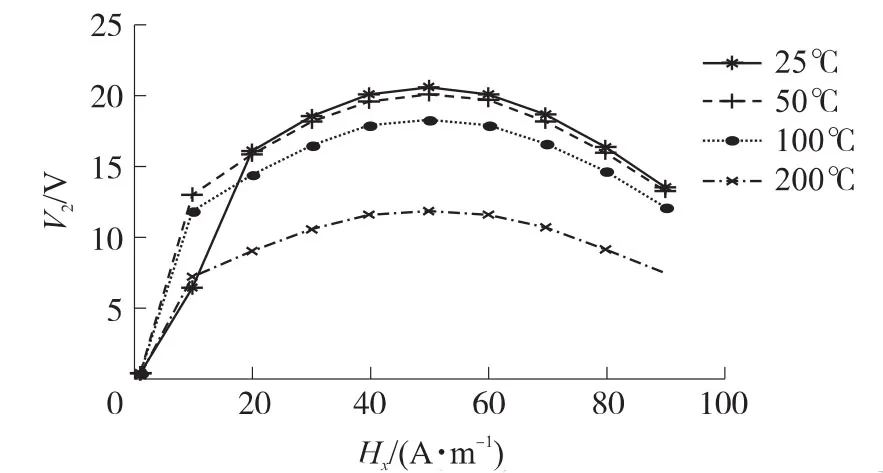
图1 温度高于常温时二次谐波点的幅值

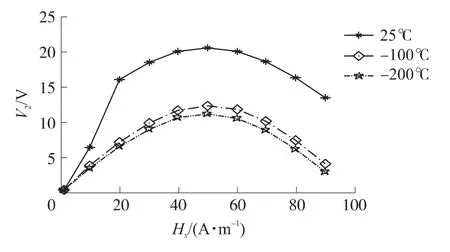
图2 温度低于常温时二次谐波点的幅值

图3 各温度下的二次谐波点的幅值

从图1、图2和图3，可以看出:①不管是在低于常温、还是高于常温的条件下，磁通门的二次谐波电压幅值都低于常温下的幅值;②随着被测磁场的增大，各个温度条件下的二次谐波电压幅值都是先增大，达到最大值之后，逐渐下降，存在一个最大值;③在低于常温的工作条件下的二次谐波电压幅值小于在高于常温的条件下的幅值。

由于退磁场的影响，铁芯内部的磁场比在空气中的外部磁场小的多。图中的横轴为理论模型被测磁场在铁芯内部的磁场，虽然看起来线性区域似乎比较小，但是由公式(其中 H为in铁芯内部磁场，Hd为暴露在空气中的外部磁场，μr为相对磁导率，Nd为退磁因子)[11]得，实际的被测磁场要大得多，按照实际模型来换算，图中的线性区域已经比较大。

其中，该实验所用钴基非晶铁芯材料的居里温度Tc=550 K，临界系数β=0.4。利用式(13)～式(16)建立HSPICE模型，验证不同温度对磁通门传感器二次谐波电压幅值的影响，归一化后，得到长条形磁通门的最终输出电压。

4 结论

本文在JA模型的基础上，引进热效应，发展了与温度有关的JA模型，增加了四个磁滞参数:自发磁化强度Ms、磁畴耦合因数α、钉住系数k、可逆磁化强度系数c，作为温度的函数。除此之外，还引入了居里温度Tc和临界系数β，作为模型的新参数。

通过 0K时的磁滞参数值 Ms(0)、k(0)、α(0)、c(0)以及 a，确定 Ms、k、α、c关于温度T 的表达式，并应用于长条形磁通门传感器中，来测试温度对其的影响。由实验结果可以得出:①随着外部被测磁场的不断增大，磁通门输出电压先增大后减小，存在一个最大的输出电压;②磁通门传感器不适宜于在低温(25℃以下)条件下工作。在低温时，铁芯材料的磁性能受到抑制，不能工作在最优的工作状态。还有一点值得注意，在居里温度以下时，磁通门显示正常的输出信号;但当温度超过居里点温度时，铁芯材料由铁磁材料转化为顺磁材料，铁芯性能会随着外磁场的变化而变化，对外磁场反应比较敏感，输出信号完全失真[12]。

该工作研究了温度对长条形磁通门输出信号的影响，与已有的实验结果吻合得很好，为磁通门的实际应用提供了有益的理论探索。

但是，也应该看到，每种铁芯材料都有其固定的温度适用范围。要提高磁通门的温度适应性，尤其是在低温条件下工作，除了寻找温度适应范围更广、稳定性更好的铁磁材料外，还可以采取温度补偿的方法来提高磁通门的适应温度范围，提高磁通门的输出性能[13－16]。

[1]李菊萍，刘诗斌，郭博，等.基于四次谐波选择法的磁通门传感器分析[J].传感技术学报，2011，24(10):1412－1415.

[2]Raghunathan A，Melikov Y，Snyder J E.Modeling the Temperature Dependence of Hysteresis Based on Jiles-Atherton Theory[J].IEEE Transactions on Magnetics，2009，45(10):3954－3957.

[3]David C Jiles，Thoelke J B，Devine M K.Numerical Determination of Hysteresis Parameters for the Modeling of Magnetic Properties Using the Theory ofFerromagnetic Hysteresis[J].IEEE Transactions on Magnetics，1992，28(1):27－35.

[4]Hans Georg Brachtendorf，Christoph Eck，Rainer Laur.Macromodeling of Hysteresis Phenomena with SPICE[J].IEEE Transactions on Circuits and Systems—Ⅱ:Analog and DigitalSignal Processing，1997，44(5):378－388.

[5]黄子平，张良.利用J－A模型模拟非线性磁芯[C]//第十届高功率粒子束学术交流会议文集.长沙:中国物理学会，2006:114－117.

[6]Jacek Izydorczyk.Extraction of Jiles and Atherton Parameters of Ferrite from Initial Magnetization Curves[J].Journal of Magnetism and Magnetic Materials，2006，302(2):517－528.

[7]Peter R William.Simulation of Magnetic Component Models in E-lectric Circuit Including Dynamic Thermal Effects[J].IEEE Transactions on Power Electronics，2002，17(1):55－65.

[8]William M C，Williams，Mark C.Simulation and Modeling of Nonlinear Magnetics[C]//Proceedings of the 1995 IEEE International Symposium on Circuits and Systems.USA:IEEE，Piscataway，NJ，United States，1995:736－739.

[9]Arrott A，Noakes J E.Approximate Equation of State for Nickel Near Its Critical Temperature[J].Phys.Rev.Lett，1967，19(14):786－789.

[10]Hauser H，Jiles D C，Melikhov Y，et al.An Approach to Modeling the Dependence of Magnetization on Magnetic Field in the High Field Regime[J].Journal of Magnetism and Magnetic Materials，2006，300(2):273－283.

[11]Koch R H，Rozen J R.Low Noise Fluxgate Magnetic Field Sensors Using Ring and Rod Core Geometries[J].Applied Letters，2001，78(6):1897－1899.

[12]NEALIS J，SMITH R C.Partial Inverse Compensation Techniques for Linear Control Design in Magnetostrictive Transducers[C]//Smart Structures and Materials 2001-Modeling，Signal Processing，and Control in Smart Structures.Newport Beach，United States:SPIE.2001:462－473.

[13]王雷，谭久彬，刘玉涛.超磁滞伸缩体内涡流效应有限元分析[J].光学精密工程，2006，14(3):445－449.

[14]李欣欣，王文，陈戬恒，等.Jiles-Atherton模型的超磁致伸缩驱动器磁滞补偿控制[J].光学精密工程，2007，15(10):1558－1563.

[15]曹林，何金良，张波.直流偏磁状态下电力变压器铁芯动态磁滞损耗模型及验证[J].中国电机工程学报，2008，28(24):141－146.

[16]刘昭元，刘诗斌.基于DSP的数字磁通门传感器设计[J].传感技术学报，2009，22(9):1280－1283.