受损伤潜艇结构剩余强度评估

白雪飞，郭日修，赵海江

（1海军工程大学，武汉 430033；2海军装备部，北京 100081）

1 引 言

潜艇的生存能力是潜艇最重要的性能。潜艇在海上作战或执行任务，可能遭受敌方武器攻击（如：水下爆炸、空中爆炸等）或遭遇碰撞等意外事故，导致艇体结构受到损伤。若受损伤的耐压船体结构出现较大变形，不再处于完好状态，但不是破损进水以致不可挽救，则在这种情况下，对受损伤后的潜艇耐压船体结构提出一个明确的、量化的“剩余强度”概念，并建立一套实用方便的“剩余强度”评估方法，对于保证潜艇的安全使用，保持潜艇的生存能力是非常必要的。

所谓受损伤的潜艇结构的“剩余强度”是指：在这种损伤状态下，潜艇耐压船体能安全下潜的最大深度。显然，表示“剩余强度”的这个最大深度，小于该潜艇在完好的、未受损伤状态下的最大深度，即极限深度。

国外如美国、俄罗斯等国在军舰破损强度研究方面做了大量工作，国内也曾针对水面舰艇破损强度做过一些理论和试验研究工作[1]，但对潜艇结构剩余强度的研究工作还较少，因而有必要开展这方面的研究工作。

本文以受损伤的潜艇耐压船体典型结构—出现损伤变形后的环肋圆柱壳舱段结构作为研究对象，以“涡形凹陷”作为因损伤而出现的变形的典型形状，将这种受损伤后的结构形状作为初始状态（零应力状态）进行分析，考察该结构在静水外压作用下的应力分布和失稳临界压力，与完好状态（设计状态）的环肋圆柱壳进行比较，分析损伤凹陷位置和范围的变化对损伤后的耐压船体所能承受的最大载荷的影响规律，为受损伤的潜艇结构的剩余强度提供一个明确的量化指标。

2 受损伤的潜艇耐压船体结构的计算模型

本文的研究对象是受局部损伤的潜艇耐压船体结构，可以取出受损伤的耐压船体所在的一个舱段—两耐压舱壁之间的受损伤的环肋圆柱壳进行研究。潜艇可能受到的损伤多种多样，受损的程度、位置和范围都是随机的，因而有必要建立一种对受损伤的耐压船体结构形状的数学描述，以便在此基础上建立对受损伤的耐压船体结构进行应力和稳定性分析的计算模型。

2.1 损伤凹陷的数学描述

实际测量结果表明，受损伤耐压船体的变形大多是局部的凹陷，采用Amazigo[2]提出的“涡形凹陷”描述损伤后的耐压船体的典型形状是比较合理的。李忠[3]改进了涡形凹陷的数学表达式，使得凹陷线形光滑，本文采用这种数学表达式来描述损伤后耐压船体的涡形凹陷的形状。

设圆柱壳半径为R，壳板厚度为t，涡形凹陷在圆柱壳母线方向的范围为S（如图1）。

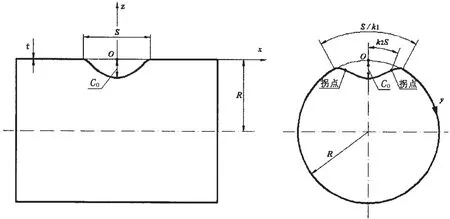
图1 损伤凹陷的描述Fig.1 Shape description of indentation

涡形凹陷的数学表达式为如下分段函数[3]：

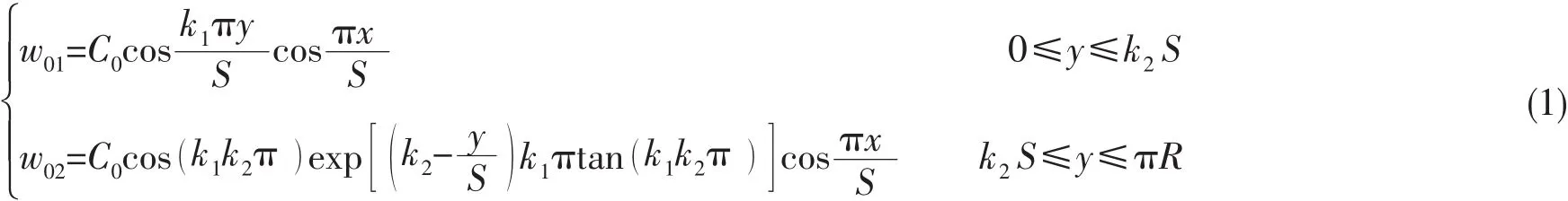
式中，x为轴向坐标，y为环向坐标（弧长坐标），涡形凹陷的最大值为C0。

涡形凹陷在环向的范围（弧长）为S/k1，拐点位置的环向坐标为k2S。可见k1反映涡形凹陷的母线方向范围和环向范围之间的比例，k2反映涡形凹陷环向拐点的位置，引入无量纲参量η表示涡形凹陷的幅值：

2.2 计算模型的建立

以带有凹陷的环肋圆柱壳舱段作为应力分析和稳定性分析的初始状态，假设在初始状态没有应力。为简化问题的分析，本文只讨论在环肋圆柱壳舱段上有一处损伤凹陷的情形，选取几种典型状态建立系列计算模型。

2.2.1 凹陷范围的选取

考虑到耐压船体所受的损伤是局部的，假设凹陷在母线方向的范围不超过2倍肋骨间距，凹陷在环向上的弧长范围与母线方向相同，即取参数k1=1，参照文献[2]，取k2=3/（8k1）=3/8。

2.2.2 凹陷幅度的选取

取 η 值为 0.25、0.5、1.0、1.5、2.0、2.5、3.0 和 3.5 等数值。

2.2.3 凹陷位置的选取

环肋圆柱壳所受局部损伤是随机的，既可能出现在肋骨及其周围的壳板位置，也可能只出现在肋骨之间的壳板上。在选取凹陷的位置时，考虑如下2种最具典型性的危险状态。

（1）凹陷位置1：凹陷中心位于肋骨位置，相邻两跨肋间壳板均发生变形，而相邻两根肋骨均无变形。这种情形模拟耐压船体上单根肋骨及与之相邻的2跨肋间壳板受到损伤的情形，这种受损状态的计算模型如图2，图中坐标原点o取在凹陷最大位置。

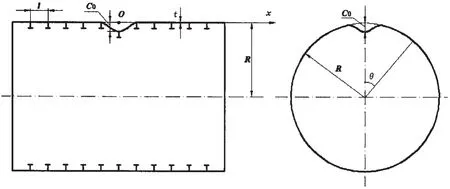
图2 损伤凹陷中心在肋骨位置Fig.2 Center of indentation at the location of ring-stiffener

（2）凹陷位置2：凹陷中心位于肋间壳板跨中，该跨肋间壳板边缘的肋骨均无损伤。这种情形模拟耐压船体壳板受损而肋骨无损伤的情形，这种受损状态的计算模型如图3，图中坐标原点o取在出现凹陷的壳板左侧的肋骨位置。

图3 损伤凹陷中心在肋间壳板跨中Fig.3 Center of indentation at the middle of shell between adjacent ring-stiffeners

运用大型商用有限元软件MSC-NASTRAN，对凹陷中心在肋骨和凹陷中心在肋间壳板跨中两种情形，按照不同凹陷幅度建立一系列有限元计算模型，分别对其进行应力和稳定性分析。

3 带有凹陷的环肋圆柱壳应力和稳定性分析

3.1 应力分析

为便于对应力计算结果进行分析，定义如下无量纲量：

式中，x为轴向坐标，l为肋骨间距。

式中，σ为计算应力，p0为完好环肋圆柱壳舱段承受的最大压力，即设计规范定义的“极限压力”，它对应于潜艇的“极限深度”。

表1 环肋圆柱壳最大应力汇总Tab.1 Max stress of ring-stiffened cylindrical shell

由表1给出的最大应力变化可知：

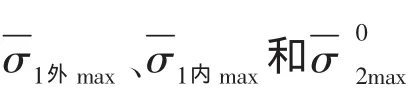
3.2 稳定性分析

分别对凹陷中心在肋骨和在肋间壳板中部两种情形的计算模型，进行失稳临界压力的有限元分析。分别计算两种模型的肋间壳板失稳理论临界压力PES和舱段总体失稳理论临界压力PET。计算舱段总体失稳临界压力时，舱段长度L与肋骨间距l之比取12，这是参照我国现役常规潜艇耐压船体舱段的尺寸选定的，L/l取更大值，PET的变化不大。凹陷中心在肋骨位置和肋间壳板跨中位置两种情形，环肋圆柱壳理论失稳临界压力和环向失稳波数如表2所示。

表2 环肋圆柱壳失稳临界压力（MPa）和环向失稳波数（m）Tab.2 Critical pressure of ring-stiffened cylindrical shell and buckling wave number

由表2给出的失稳临界压力变化可知：

（1）带有凹陷的环肋圆柱壳肋间壳板失稳和舱段总体失稳理论临界压力PES和PET均低于完好环肋圆柱壳。凹陷幅度η在0.25～3.5范围变化，凹陷中心在肋骨位置时，PES和PET最大降低为完好状态理论临界压力的0.897和0.981倍；凹陷中心在肋间壳板时，PES和PET最大降低为完好状态理论临界压力的0.986和0.991倍。

（2）肋间壳板失稳理论临界压力PES显著低于舱段总体失稳理论临界压力PET，故凹陷中心在肋骨位置的环肋圆柱壳只可能出现肋间壳板失稳。

（3）PET值随着η的增大而单调减小，这是由于凹陷幅度越大，环肋圆柱壳舱段初始缺陷越大，舱段总体失稳也越容易发生。PES值随着η的增大而减小到某个最小值后，随着η的进一步增大，PES值值反而会增大。分析其原因是，当η值较大时，出现凹陷的壳板转化为一个双曲率扁壳结构，相对于完好圆柱壳结构而言，其局部稳定性反而有所提高。观察计算模型的失稳模态（此处略）也可看出，当η值较大时，肋间壳板失稳波形主要出现在凹陷以外的区域，因而导致肋间壳板失稳临界压力随凹陷幅度的增大而略有提高。

4 受损伤潜艇结构剩余强度指标的确定

4.1 受损伤潜艇结构剩余强度指标的建立

4.1.1 与应力相关的剩余强度指标的建立

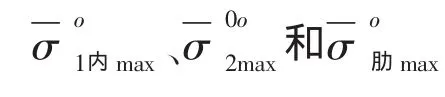
上式中，使用了R外纵、R内纵、R中环和R肋骨4个折减系数，这是因为这些应力出现在受损伤的耐压船体的不同的位置，（4）式的4个条件一般不能同时满足。

今定义受损伤潜艇结构的剩余强度指标R为受损伤潜艇耐压船体（η≠0）能承受的最大静水压力（对应于能安全下潜的最大深度）与完好潜艇（η=0）能安全承受的最大静水压力（对应于“极限下潜深度”）之比，即：

由（4）式可知，R为（4）式4个折减系数中的最小者，它们是：

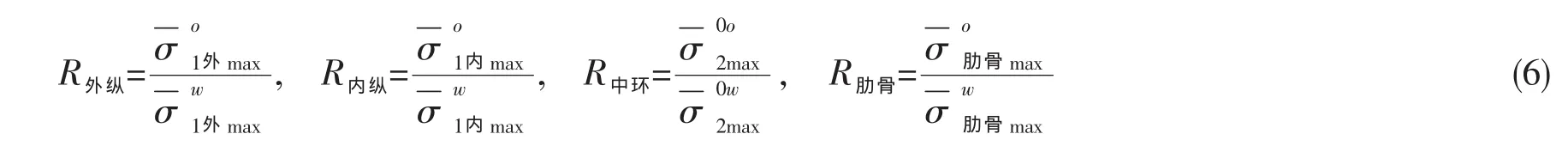
按（6）式计算的R外纵、R内纵、R中环和R肋骨中的最小者，即为受损伤潜艇耐压船体结构与应力相关的剩余强度指标，即：

式中R表明受损伤的潜艇耐压船体在静水外压力Rp0下，结构的最大应力仍处于安全的范围。

4.1.2 与稳定性相关的剩余强度指标的建立

带有凹陷的环肋圆柱壳结构不再是轴对称薄壳结构，其失稳临界压力的几何非线性和物理非线性修正目前暂无规范可循，故不能计算出值。为反映带有凹陷的环肋圆柱壳与理想环肋圆柱壳失稳临界压力之比，近似地采用理论失稳临界压力之比来代替修正后的失稳临界压力之比，即定义：

式中稳定性剩余强度系数R失稳表示：受损伤的潜艇耐压船体，在静水外压力R失稳作用下，结构能保持稳定性。由表2结果可知，带有凹陷的环肋圆柱壳肋间壳板失稳临界压力（PES）均明显低于舱段总体失稳临界压力（PET），故不可能出现舱段总体失稳，只可能出现肋间壳板失稳，因而带有凹陷的环肋圆柱壳理论失稳临界压力（）取肋间壳板失稳临界压力（PES）值（如表 2）。

4.2 受损潜艇剩余强度系数的变化图谱

运用第3节得出的应力和稳定性计算结果（如表1、表2），根据（6）式和（9）式可分别计算出剩余强度系数R外纵、R内纵、R中环、R肋骨和R失稳。两种凹陷位置对应的剩余强度系数值如表3所示。

表3 环肋圆柱壳剩余强度系数Tab.3 Residual strength coefficient of ring-stiffened cylindrical shell

比较 R外纵、R内纵、R中环、R肋骨和 R失稳的数值可以看出：对于一定的 η 值，R外纵、R内纵、R中环、R肋骨总是低于相应的R失稳，这表明：受损伤潜艇耐压船体的剩余强度是由应力控制而不是由稳定性控制。由表3还可看出，随着η的增大，R外纵、R内纵、R中环、R肋骨中有些数值不仅不降低，反而随之增大，则在判断结构的剩余强度时，应取相应的R的最低值。例如：对于凹陷中心在肋间壳板的情形，当η=1.5时，R内纵=0.521；当 η=2.0 时，R内纵=0.554（>0.521），则此时 R内纵应取 0.521，即在表中斜体加粗的数值应取其上面的最低值。按照这样的取法得出的潜艇结构剩余强度是偏于安全的。

由此可做出 R外纵、R内纵、R中环、R肋骨和 R失稳变化图谱如图 4、图 5 所示。

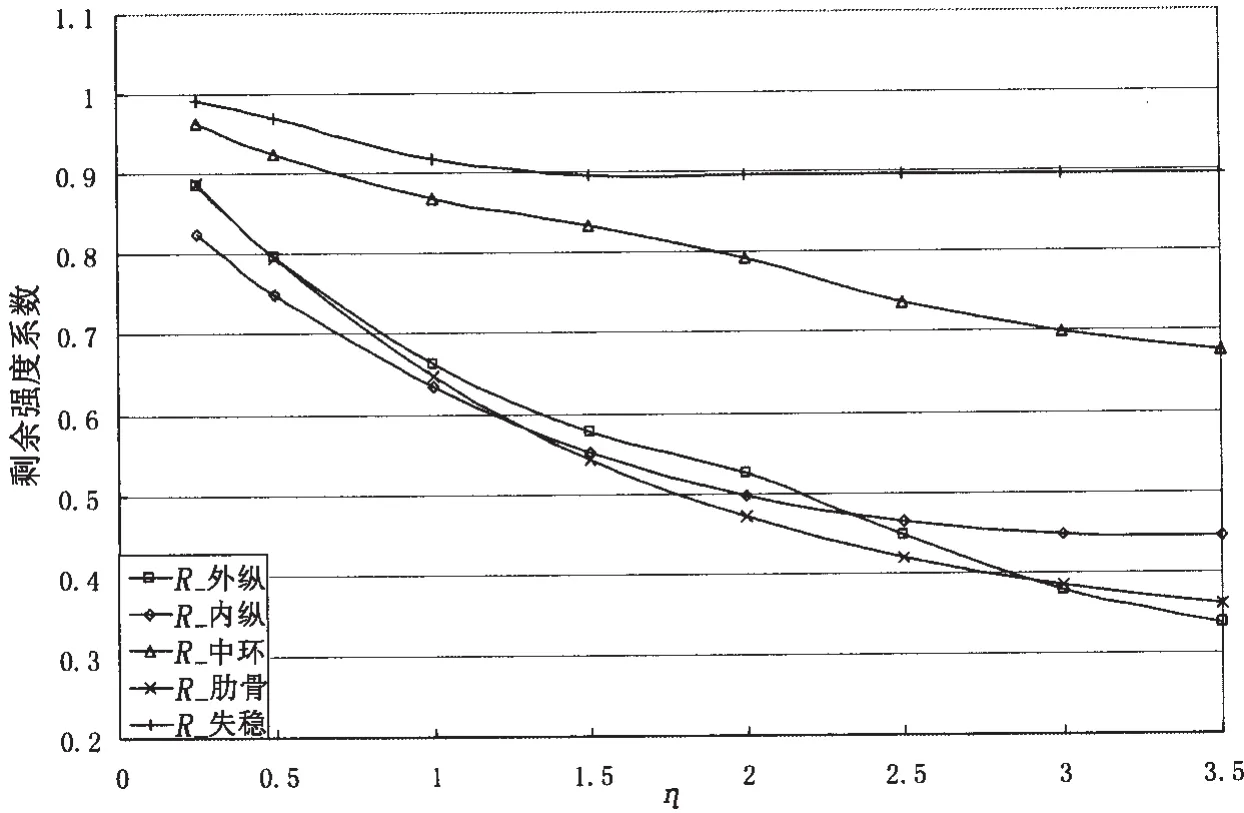
图4 凹陷中心在肋骨位置时潜艇结构剩余强度系数变化图谱Fig.4 Residual strength coefficient curves of submarine structure when the center of indentation at the location of ring-stiffener

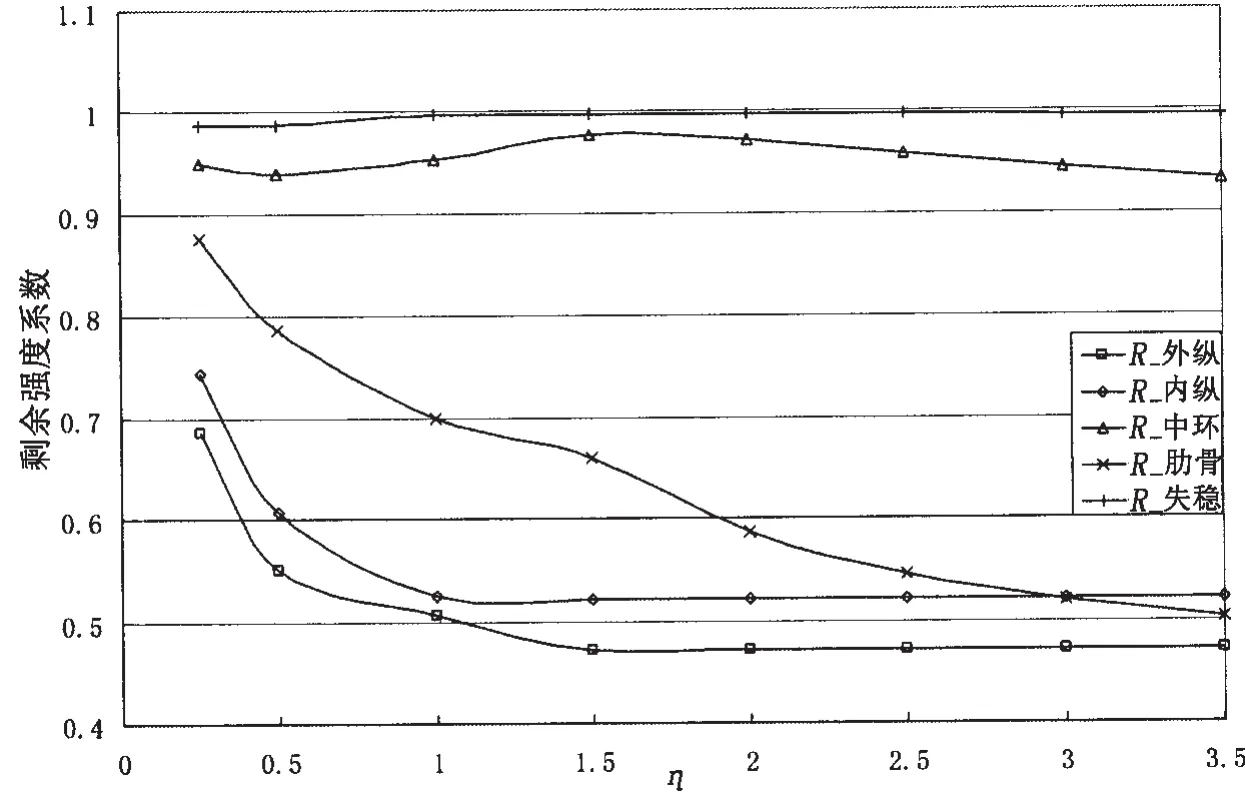
图5 凹陷中心在肋间壳板位置时潜艇结构剩余强度系数变化图谱Fig.5 Residual strength coefficient curves of submarine structure when the center of indentation at the middle of shell between adjacent ring-stiffeners

4.3 利用剩余强度系数图谱估算潜艇结构剩余强度

与应力相关的剩余强度系数R外纵、R内纵、R中环、R肋骨和稳定性剩余强度系数R失稳，表示受损伤的潜艇结构分别基于应力或基于稳定性分析所能安全承受的最大压力与完好潜艇的极限压力之比，从它们中选择最小者，即为受损伤的潜艇的剩余强度系数。它表示受损伤的潜艇耐压船体能安全承受的最大压力与完好潜艇的极限压力之比。剩余强度系数的下标表示其剩余强度由下标表示的应力或稳定性控制。

潜艇耐压船体结构遭受损伤后，首先考察损伤的幅值，由此计算无量纲参数η，再考察损伤最大点的位置是位于肋骨或是肋间壳板，查阅相应的剩余强度系数图谱，其中的最小值（如：R肋骨）即表示受损伤耐压船体能安全承受的最大压力与完好的耐压船体极限压力之比，亦即表示受损伤潜艇能安全下潜的最大深度与完好潜艇极限深度之比，从而得出受损潜艇结构的剩余强度。

5 结 论

（1）潜艇遭受武器攻击或遭遇意外事故时，若耐压船体结构局部出现较大变形但未破损进水，则潜艇结构仍具备一定的承载能力，仍可在一定范围内安全下潜。这种损伤状态下，潜艇能安全下潜的最大深度，我们称之为受损伤的潜艇结构的“剩余强度”。

（2）通过考察带有损伤凹陷的环肋圆柱壳在静水外压作用下的应力和稳定性，与相应的完好状态（设计状态）的环肋圆柱壳进行比较，提出了“剩余强度系数”概念，为受损伤的潜艇结构的“剩余强度”提供了明确的量化指标。

（3）以带有损伤凹陷的环肋圆柱壳舱段结构作为研究对象，分析了损伤凹陷位置和范围的变化对受损伤的耐压船体所能承受的最大载荷的影响规律，得出了“剩余强度系数图谱”。运用该图谱可方便快速地得出当前潜艇能安全下潜的最大深度，避免出现更大的危险。

[1]熊建武,郭日修.船舶结构剩余强度的研究进展[J].海军工程学院学报,1999(2):9-15.

[2]Amazigo J C,Fraster W B.Buckling under external pressure of cylindrical shells with dimple shaped initial imperfections[J].International Journal of Solids and Structure,1971,7(11).

[3]李 忠.具有初始挠度的环肋圆柱壳在静水外压作用下的应力分析[D].武汉:海军工程学院,1985.