储液容器内液体自由晃动的有限元分析

贾善坡 ， 许成祥

（1长江大学 城市建设学院，湖北 荆州 434023；2山东大学 岩土与结构工程研究中心，济南 250061）

1 引 言

液体的晃动问题在船舶、航天、石化、高层建筑减振和城市供水等领域均有应用，具有广泛的工程背景。在液固耦合系统动力学的研究中，液体晃动动力学是必须的基础。容器液体晃动和控制问题的研究受国内外研究人员的广泛重视，主要研究液体自由晃动的固有频率，在激励下液体的受迫晃动以及它对贮箱的作用力，贮箱与液体晃动之间的耦合动力学问题，液体晃动的等效力学模型，液体晃动研究的工程方法，液体大幅度晃动等课题[1-4]。到目前为止，仅求出了少数特殊形状容器内液体晃动特性的解析解，对于一般形状的容器，多采用数值方法求解。目前，出现一批数值求解液体晃动的成功方法，如有限差分方法、有限元法、边界积分法和边界元法等[5-7]。具有代表性的研究方法有：王照林等[4]针对液体非线性晃动的一些定性理论以及稳定性问题进行了较为系统的研究；李遇春等[8]利用边界元方法对液体非线性晃动问题进行了数值分析；包光伟等[9]采用VOF方法对液体晃动进行了数值仿真；周宏等[10]采用任意拉格朗日—欧拉（简称ALE）方法对带有自由液面的晃动问题进行了分析讨论；尚春雨等[11]提出用FLUENT计算液体晃动问题的方法；刘富等[12]采用SPH方法对棱形液舱在外加激励作用下，不同充液比工况所对应的舱内液体晃动进行了三维数值模拟，并将其与实验进行对比，两者吻合较好，同时成功地模拟出液体晃动产生的波浪翻卷和破碎；李青等[13]推导了任意三维贮箱内液体晃动的等效力学模型，采用有限元方法建立计算等效力学模型参数的数值算法，利用矩阵相似变换的性质分离液体零频以消除液体刚度矩阵的奇异性，并采用商用分析软件FLOW-3D验证了等效力学模型的有效性。

容器内液体的晃动问题，可以归结为两种类型：一是特征值问题，求解容器内液体晃动的自然频率，是进一步研究液体晃动问题的基础。第二类型是研究在外界扰动下，容器内液体的反应。数值模拟液体的晃动实际上就是用数值方法求解带有自由边界的非定常流体的动力学问题，由于自由液面的位置是未知的，而且自由液面边界条件是复杂的非线性方程，因此，具有自由液面的流体的流动是用数值方法求解的最困难的问题之一。当贮液结构（容器）具有大的空间刚度时，可忽略器壁的弹性变形，将容器近似为绝对刚体。本文建立了可压缩液体自由晃动的特征方程，并提出了相应的有限元计算方法，计算过程中假定容器壁面是刚性的，液体在固—液界面上沿法线方向的分速度为零，在晃动自由面上忽略了液体的表面张力。

2 基本方程

设液体为无旋无粘性的，计及流体的可压缩性，则液体在域V内满足连续性方程、运动方程和状态方程，即：

式中，上标“·”表示对时间的求导，vi是流体扰动的流体速度分量，ρ0是扰动前流体的密度，ρ和p分别是扰动引起的密度变化和流场压力变化，c0是流体中的声速，表示为：

式中k为流体的体积模量。

将容器壁简化为刚性的，流体在容器湿表面∂Vw（固壁边界）上满足不可渗透性条件，在自由面∂Vf（自由面边界）上满足运动学边界条件和动力学边界条件，则三维容器内液体晃动特征问题满足下列方程和边界条件[1，4]：

式中，g是重力加速度，V、∂Vf和∂Vw分别是液体域、液体自由面边界和腔壁边界。

3 液体晃动问题的有限元模型

对流体采用压力格式，则单元内的压力分布可表示为：

同样可以形式上将液体域V上的解函数写成如下形式：

式中，（p1,p2,…,pn）是液体域V上的所有节点变量。

对（3）式利用Galerkin法形成求解方程，即：

对（6）式中的V∫δp（ p,ii）dV项进行分部积分，可得：

考虑到δp的任意性，将（5）式代入（7）式，则可得到液体自由晃动问题的有限元方程，

式中，p为流体节点压力向量，Mf和Kf分别为流体质量矩阵和流体刚度矩阵，具体表示式为：

方程（8）的解假设为如下形式：

式中，z是n阶向量，ω是向量z的振动频率，t为时间变量，t0是由初始条件确定的时间常数。将（11）式代入方程（8），可以导出液体自由晃动问题的特征方程：

其中，固有频率 ωj（j=1,2,…,n）对应于固有模态列阵zj。

对于三维液体晃动问题，系统自由度相当多，计算中耗时、耗费及求解困难。因此，有必要采用缩减技术来分析三维液体晃动问题，缩减技术可以减少系统的自由度，节省计算和分析的耗费[14-15]。将p写为p=[pm, ps]，（8）式可写为：

式中，下标m表示保留的主自由度，而s表示被缩减掉的副自由度。

假设副自由度质量表示的惯性力很小前提下，有：

就有：

由此得：

根据系统动能和势能在缩减前后不变，有：

由此可导出缩减后质量、刚度矩阵为：

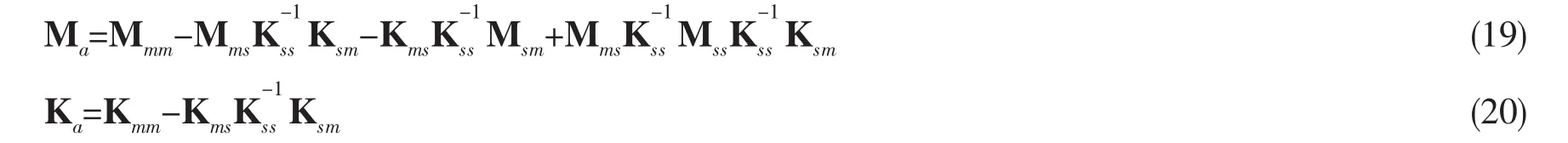
因此，系统的振动方程变为：

平衡方程组数目由原来的n降为所选择的主自由度数m了。

4 计算实例

考虑一圆柱形的刚性含液容器，容器底部固定（见图1）。主要几何及力学参数为：油罐半径R=40m，充液高度h=30m，流体密度ρ0=1 000kg/m3，重力加速度g=9.8m/s2，声速 c0=1 435m/s（流体体积模量 2.06GPa）。

假定储罐是刚性的，液体是可压缩的，地面运动为水平平移运动，没有旋转分量。液体对流晃动模态是基于Laplace等式的第二项的线性解求得[1]：

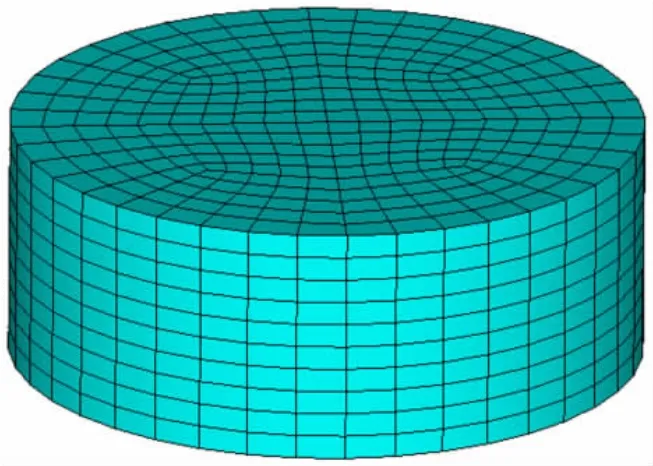
图1 圆柱形容器内液体晃动的有限元模型Fig.1 The finite element model of liquid sloshing in cylindrical container

式中， fi为液体晃动第 i阶频率（单位：rad/s）；λi为一阶Bessel函数导数的第i个根；g为重力加速度；R为储罐半径；h为液体高度。

4.1 自由晃动分析

通过（22）式获得的前几阶液体自然晃动频率的理论解如表1所示。采用本文所介绍的有限元法计算液体的自然晃动频率及液面晃动形式，两种计算方法获得的结果比较如表1，有限元所得的液面晃动形式如图2所示。

在表1中，m和n分别代表横截面内两个相互垂直方向上的半波数，由表1的计算值和理论解比较，结果令人满意，可见本文所提出的有限元法是十分有效和可靠的。

表1 刚性容器内流体自由晃动频率计算结果比较（单位：rad/s）Tab.1 Results calculated by finite element method and theoretic solution

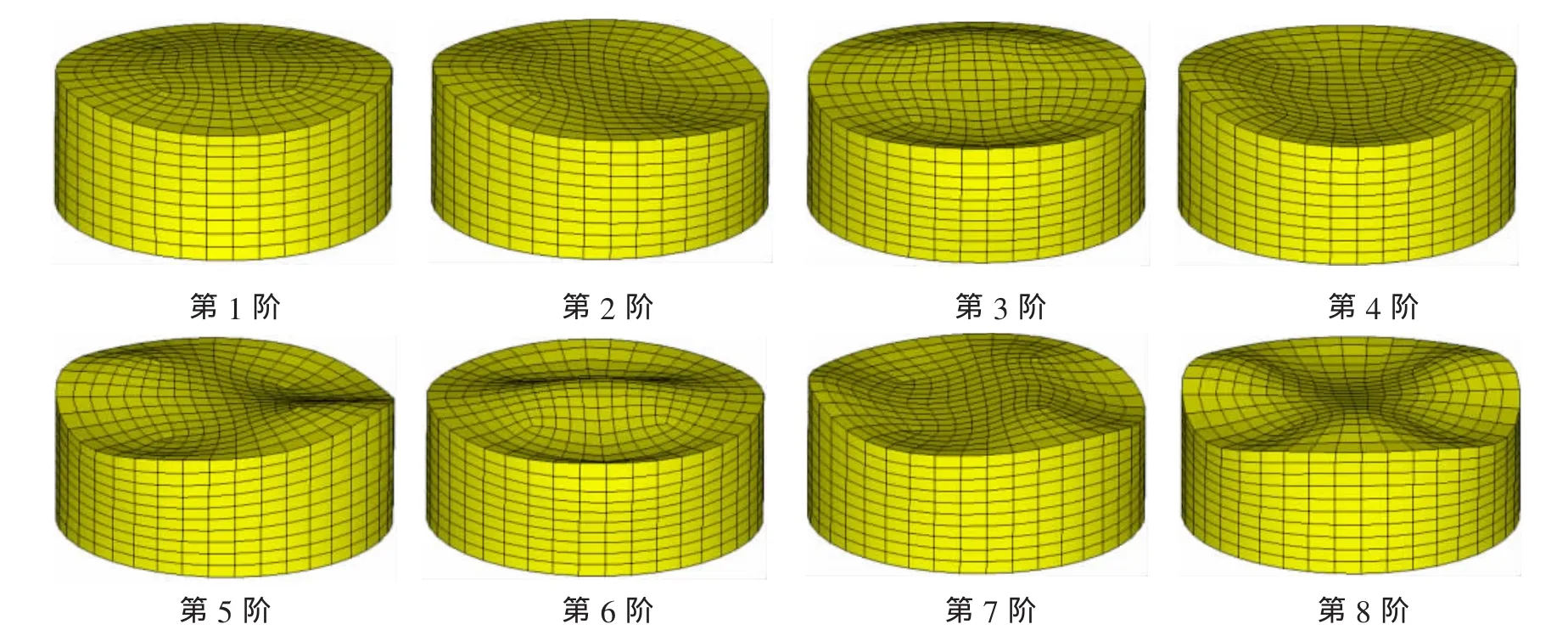
图2 流体自由表面波动模态图Fig.2 Modal characteristics of liquid sloshing in cylindrical container

从特征值计算得到的频率值以及相应的模态分析可知，流体频率实际上是由低频和高频两部分组成的。低频部分对应于流体自由表面波动，此时流体动压力仅在自由表面附近不为零，在流体内部为零。高频部分则对应于由于流体可压缩性引起的内部动压力波动，而在自由表面处动压力为零。如果在计算中不考虑流体自由表面波动，则特征值计算的结果将只能得到高频部分。如果要想获得更多阶的低频，则需将横截面内的网格加密。另外，还对不同压缩性（即不同声速）时的情况进行了计算，结果发现流体压缩性对自由表面波动部分的频率基本无影响，而对高频部分（对应于内部压力波动）的影响则很大，而且频率值与声速近似成正比关系，这意味着当考虑流体为不可压缩（即声速无穷大）时，这部分频率也将为无穷大。

4.2 晃动频率与容器半经的关系

为了揭示液体晃动频率与容器半经的关系，保持充液深度h=30m不变，改变容器半经，得出了前几阶自然晃动频率，以前4阶固有频率为例，画出f-R关系曲线，如图3所示，研究液体晃动频率与容器半径之间的关系，可以看出，随着容器半径的增大，液体晃动频率逐渐减小，液体晃动频率与容器半径基本上成反比例关系。

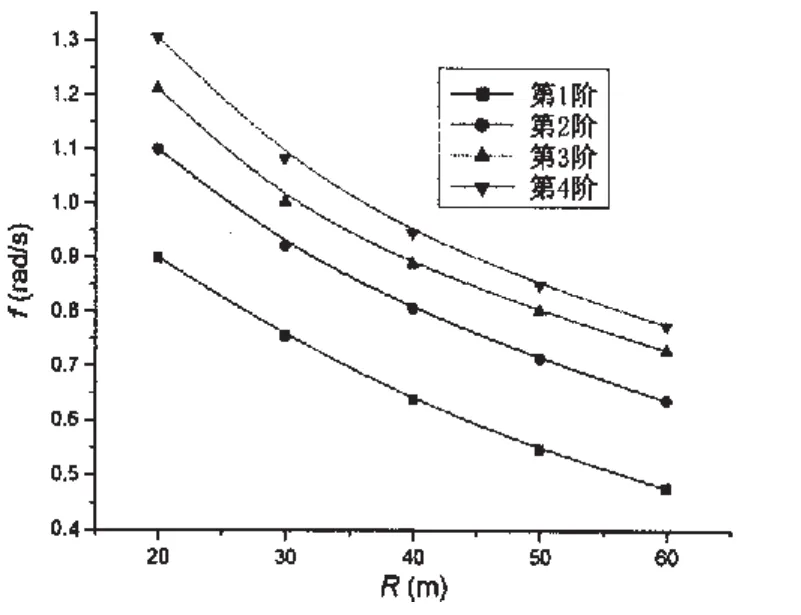
图3 液体晃动频率与容器半径的关系Fig.3 Liquid sloshing frequencies versus the radius of container

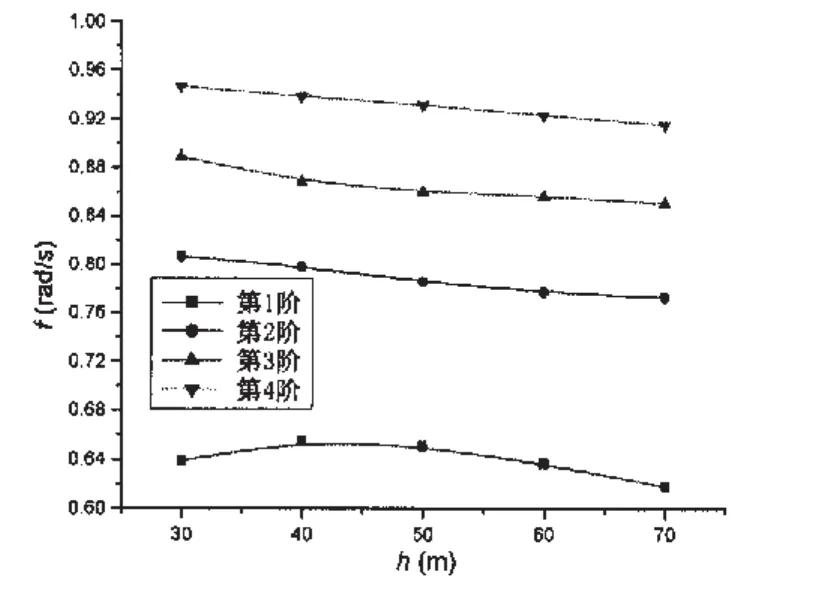
图4 液体晃动频率与液体深度的关系Fig.4 Liquid sloshing frequencies versus the depth of liquid

4.3 晃动频率与充液深度的关系

为了揭示液体晃动频率与充液深度的关系，保持容器半经R=40m不变，改变充液深度，得出了前几阶自然晃动的频率。图4表示出半径不变的容器其内部液体自然晃动的频率，随着液面高度变化而发生变化的趋势，横坐标表示深度h，纵坐标表示各阶频率值。计算结果表明，容器内液体的充满程度即液面的高度h对液体晃动频率也有很大的影响，液体深度对晃动频率的影响很明显。总体上说，对于第1阶频率来说，当充液深度达到40m时，频率达到最大值，随后，随着充液深度的增大，而频率逐渐减小；对第2阶频率来说，当充液深度达到20m时，频率达到最大值，随后，随着充液深度的增大，而频率逐渐减小；对第3、4阶频率来说，随着充液深度的增大而频率逐渐减小。

5 结 论

本文采用有限元法建立了圆柱形容器内液体晃动问题的数值计算方法，假定容器壁面是刚性的，在晃动自由面上忽略了液体的表面张力，采用缩减法来分析容器内液体的晃动动力特性问题，该方法可适用于复杂形状容器内液体的晃动问题。由计算实例的结果可知，应用有限元法计算能够求得容器内液体自然晃动的各阶频率和振型，且具有较高的精确度，该方法可以应用于三维任意形状容器内液体的晃动问题求解。在设计中如何考虑液体晃动的影响以及如何抑制液体晃动，仍是一个值得研究的课题，此外，将液体晃动问题与结构弹性体振动问题统一起来就可以应用有限元法求解液体-结构耦合问题。

[1]贾善坡.大型储罐地基变形特性研究及储液晃动分析[D].东营:中国石油大学(华东),2006.

[2]许成祥,贾善坡.储罐结构有限元动力模型修正及参数辨识研究[J].武汉理工大学学报,2010,32(9):286-290.

[3]廖乐康,张圣坤.承船厢二维非线性晃动的分析[J].船舶力学,2006,10(2):47-55.Liao Lekang,Zhang Shengkun.Analysis on 2-D nonlinear slosh of ship-chamber[J].Journal of Ship Mechanics,2006,10(2):47-55.

[4]王照林,刘延柱.充液系统动力学[M].北京:科学出版社,2002.

[5]杜 颖,刘习军,贾启芬.液固耦合动力学问题的研究[J].机床与液压,2004(11):9-12.

[6]Liu Dongming,Lin Pengzhi.A numerical study of three-dimensional liquid sloshing in tanks[J].Journal of Computational Physics,2008(227):3921-3939.

[7]Mitra S,Sinhamahapatra K P.2D simulation of fluid-structure interaction using finite element method[J].Finite Elements in Analysis and Design,2008(45):52-59.

[8]李遇春,楼梦麟.渡槽中流体非线性晃动的边界元模拟[J].地震工程与工程振动,2000,20(2):51-56.

[9]包光伟,王振强,张天翔,等.火箭推进剂液体晃动关机响应的数值仿真[J].宇航学报,2002,23(2):84-88.

[10]周 宏,李俊峰,王天舒.用ALE有限元模拟的网格更新方法[J].力学学报,2008,40(2):267-272.

[11]尚春雨,赵金城.用FLUENT分析刚性容器内液面晃动问题[J].上海交通大学学报,2008,42(6):953-956.

[12]刘 富,童明波,陈建平.基于SPH方法的三维液体晃动数值模拟[J].南京航空航天大学学报,2010,42(1):122-126.

[13]李 青,马兴瑞,王天舒.非轴对称贮箱液体晃动的等效力学模型[J].宇航学报,2011,32(2):242-249.

[14]赵玉成,张亚红,白长青,许庆余.固体火箭发动机模态分析的缩聚方法[J].固体火箭技术,2004,27(2):98-100.

[15]朱安文,曲广吉,高耀南.航天器结构动力模型修正中的缩聚方法[J].中国空间科学技术,2003(2):6-10.