基于格型递归最小二乘算法的船舶运动极短期预报

彭秀艳，刘长德

（1哈尔滨工业大学航天学院，哈尔滨 150001；2中国船舶科学研究中心，江苏 无锡 214082）

1 引言

目前，国内外对船舶运动极短期预报都非常重视并展开了许多研究。其中利用时间序列分析法[1]对船舶运动进行极短期预报越来越受到重视，这种方法的最大优点是无需知道海浪的任何先验信息和船舶航行姿态的状态方程，仅仅利用历史数据寻求规律进行预报。这种方法假设船舶在海浪中的运动姿态为一平稳的窄带随机过程，从而利用线性模型[2-5]拟合这一过程。

实际应用中，尤其是在极短期预报当中，实时预报[6-7]是我们比较关心的问题。自适应模型在某种程度上能够实时地根据量测数据和期望输出自行调整模型参数，并随着数据的陆续到来，通过递推算法自动地对模型参数加以修正，使其接近某种最佳值，即便在尚不完全掌握序列特性的情况下也能得到满意的模型。由于应用递推算法，自适应模型的参数在每次迭代中要加以修正，因此参数和输入数据是有关的，这意味自适应模型是非线性的，但习惯上也说是线性自适应模型，这指的是被估计的参数向量是由一组观察数据的线性组合进行自适应计算得出的[2-4]。

本文在最小二乘方法的基础上，提出了基于格型实现的RLS算法（LRLS），该算法结构是模块式的多极格型结构，RLS算法的结构形式是横向滤波器，因此LRLS算法可以根据需要简单地增加一级或多级格形结构而不影响原来的计算。LRLS算法的计算量和阶数n成线性关系，而RLS算法计算量是随n2增加的。LRLS降低了一般RLS算法的计算复杂度，收敛速度快，该算法的鲁棒性和收敛性都比较好，是一种理想的自适应递推方法。

2 预报算法

2.1 RLS算法

设t时刻模型的输入为X（t）=[x（t）,x（ t-1）,…,x（ t-n+1）]T，ε （t）是希望值y（t）与估计值y＾（t）之差，φ（t）= [φ1（t）,φ2（t）,…,φn（t）]T为最小二乘意义下的最优解，则有：

估计误差为

最小二乘的性能指标是使J（t）最小，

式中λ为指数加权因子，由∂J/∂φ=0可以得出确定最小二乘意义下最优解（t）的正规方程

其中n×n相关阵N（t）和n×1互相关阵M（t）分别为：

利用矩阵求逆引理[8]可求得（t），且在t=1,2,…过程中是递推式进行。

初始设定P（0）=δ-1I，（0）=0，I为单位阵（t=1,2,…）。

2.2 前向预报与后向预报

如果预报是根据t-1，…，t-n时刻的数据预报t时刻的值，可称为前向预报，如果由t，t-1，…，t-n+1时刻的数据预报t-n时刻的值，则称为后向预报。表1给出了RLS线性估计与前向、后向预报各种变量之间的对应关系。

表1 RLS线性估计与前向、后向预报各种变量对照表Tab.1 The variables about RLS linear estimation,forward prediction and backward prediction

由表1中的对应关系以及RLS算法公式可得前项预报的参数递推公式。

与前向预报器类似，推导给出反向预报的参数递推公式如下：

反向（后验）预报误差加权平方和最小值的递推公式为

2.3 LRLS算法

2.3.1 阶数更新

令标量

可推得两个按阶数递推关系式：

其中：Γf,n（t）和Γb,n（t）分别称为正向和反向反射系数，进一步可得正向和反向后验误差按阶数递推的公式如下：

以上二式可用信号流图1表示。

图1 LRLS预报误差递推结构Fig.1 Recursive structure of predicted errors about LRLS algorithm

阶数n是可变的，它取为0,1,…,N（N是预报阶数的终值）。当n=0时没有对输入数据作任何预报，这相当于初始值

当阶数由零变到N可得多级最小二乘格型滤波器如图1，所含格型结构的级数即为滤波器的阶数。

2.3.2 时间递推

为了使得上述递推依时间进行自适应递推，须导出前面计算中所需的Δn-1（t）参数按时间递推的公式，可推得Δn-1（t）按时间递推的关系如下

由正向先验误差与正向后验误差的关系也可将上式写为

其中，γ（n-1）

t为变换因子，对于正向线性自适应预报有

对于反向线性自适应预报有

3 船舶运动自适应预报模型

3.1 AR预报模型

自回归（AR）模型。

其中：p 为自回归阶数，φ1，φ2，…，φp为自回归系数，εt为零均值的正态分布噪声。

将AR模型变换成（27）式，则AR模型参数可由反射系数求得[9]。

其中l=1,2…为预报步数。应用AIC准则确定阶数p[9]，当阶数p确定，已知时，便可利用（28）、（29）式和（30）式对船舶运动进行多步预报。

3.2 模型参数递推估计

由于AR（n）模型类似于n阶线性预报器，因此LRLS参数估计公式可应用于AR模型。从t=1开始，按阶数n=1,2…,N顺序计算（N是最小二乘格形滤波器的最高阶数）。

归纳得LRLS算法的初始化如下：

（1）在t=0时算法的初始化取：

（2）对每个t≥1的零阶变量取：

4 仿真实例

仿真所用数据为某船在90°横浪、135°斜浪和180°顶浪航行状态下的横摇运动时间序列，采样频率为2Hz，对未来15s（即l=30步）进行预报，其预报曲线如图2～4，拟合误差收敛曲线如图5所示。预报性能指标用η表示：

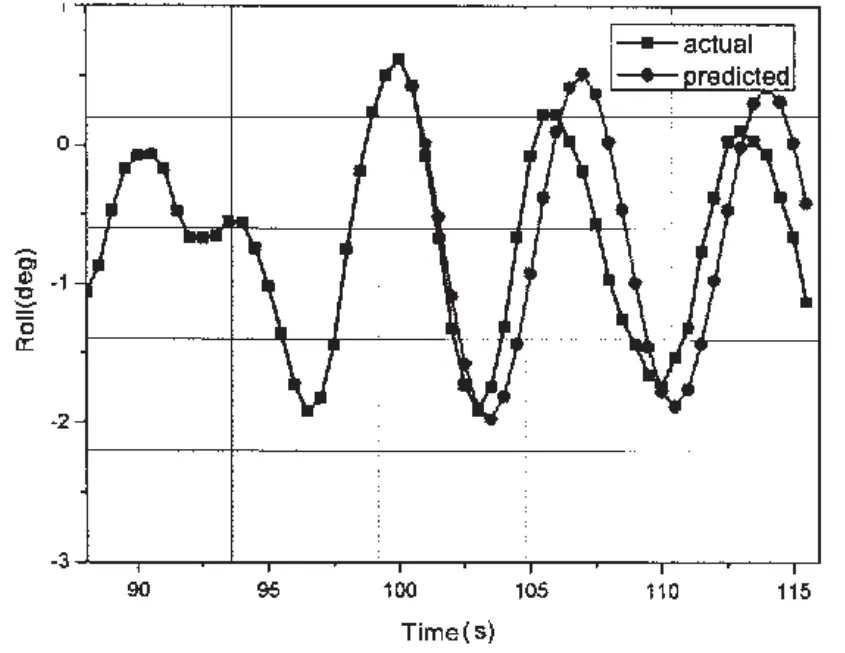
图2 顶浪（180°）横摇运动预报曲线Fig.2 The curve of predicted results(head sea)

图3 斜浪（135°）横摇运动预报曲线Fig.3 The curve of predicted results(oblique sea)

图4 横浪（90°）横摇运动预报曲线Fig.4 The curve of predicted results(beam sea)

图5 拟合误差收敛曲线Fig.5 Convergence curves of fitting errors

由表2可以得出，基于LRLS算法的自适应AR预报模型预报效果要明显好于RLS算法，在对斜浪（135°）的横摇预报效果相对要好于顶浪（180°）与横浪。随着时间的增加，预报精度逐渐下降，尤其在横浪工况下，横摇预报结果的相位、幅值与实测值差别较大。由图5可以看出，LRLS算法收敛速度较快，因而可在小样本情况下实现自适应递推预报。

为进一步验证本文自适应预报模型的预报效果，利用预报精度EPA[10]来进一步对斜浪（135°）横摇运动数据进行分析来说明基于LRLS算法的预报效果与实时预报的可行性。

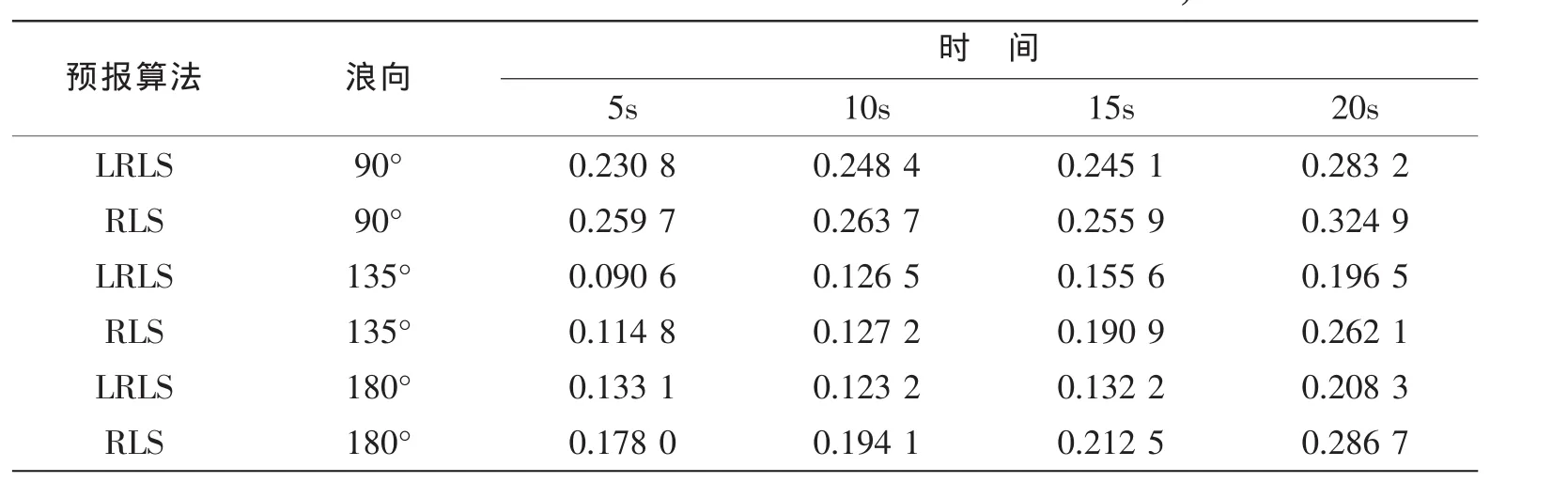
表2 基于RLS、LRLS算法的AR模型预报结果Tab.2 Prediction results about AR model based on RLS,LRLS

由表3可以得出，在相同工况下，对于不同的样本数据，预报精度相差不大，随着预报时间的增加，EPA随预报步数逐渐减小，表明预报值逐渐偏离实测值，从而预报性能随预报时间长度而下降，预报时间在10s时，精度仍可达0.85以上。在预报过程中，我们采用滑动窗法，即始终用200个数据递推建立自回归模型，预报未来15s的数据，在普通计算机上运行的时间是0.207s。远小于采样时间0.5s。因此在下一个新数据到来之前，未来15s的数据已经预报得到，随着新数据的不断到来，利用自适应算法不断修正得到新的自回归模型进行超前预报，从而保证所建立的自适应预报模型始终是最优的。

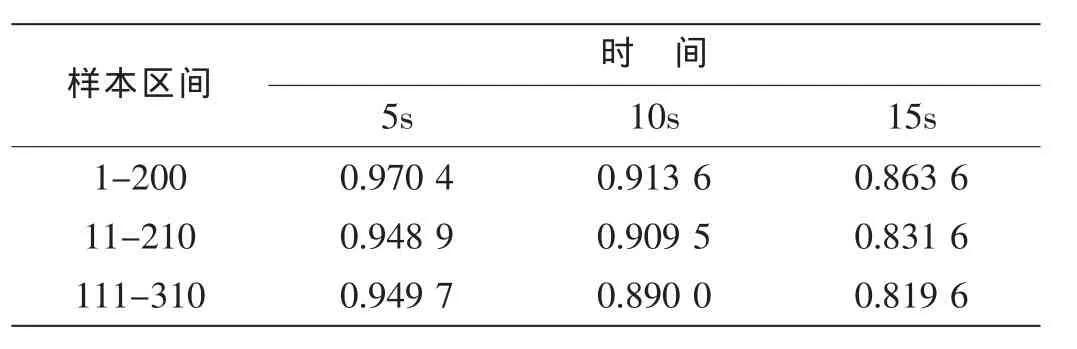
表3 预报精度EPATab.3 Prediction precision E

6 结 论

本文在RLS算法的基础上，利用LRLS算法良好的鲁棒性与收敛性，建立了基于LRLS算法的AR自适应预报模型，并将其应用到船舶运动极短期预报中。通过不同样本数据的验证分析，表明本文建立的自适应预报模型可有效地提高船舶运动的预报精度，并验证了实时预报的可行性，为工程实用化提供了理论依据。

[1]杨叔子,吴 雅,轩建平,等.时间序列分析的工程应用[M].武汉:华中科技大学出版社,2007:387-396.

[2]彭秀艳,赵希人,高奇峰.船舶姿态运动实时预报算法研究[J].系统仿真学报,2007(1):267-269.

[3]赵希人,彭秀艳,沈 艳,等.舰船运动极短期建模预报的研究现状[J].船舶工程,2002(3):4-9.

[4]马 洁,刘小河,李国斌,等.大型舰船纵摇运动的多层递阶预报[J].船舶工程,2006,28(1):5-7.

[5]马 洁,李国斌.船舶横摇运动的时间序列预报[J].北京机械工业学院学报,2006,21(1):4-7.

[6]Khan A,Bil C,Marion K E.Theory and application of artificial neural networks for the real time prediction of ship motion[C].Knowledge-Based Intelligent Information and Engineering Systems.9th International Conference,KES 2005.2005,1064-9.

[7]Broome D R,Pittaras A.Ship motion prediction[C].Proceedings of the International Offshore Mechanics and Arctic Engineering Symposium,1990,1:303-311.

[8]Diniz Paulo S R著.刘郁林,景晓军,谭刚兵等译.自适应滤波算法与实现[M].第二版.北京:电子工业出版社,2004:96-107.

[9]杨位钦,顾 岚编.时间序列分析与动态数据建模[M].修订版.北京:北京理工大学出版社,1988:417-438.

[10]韩 敏.混沌时间序列预测理论与方法[M].北京:中国水利水电出版社,2007:239-241.