基于CFD和响应面方法的最小阻力船型自动优化
2012-06-07钱建魁毛筱菲王孝义恽秋琴
钱建魁,毛筱菲,王孝义,恽秋琴
(1武汉理工大学,武汉430063;2中海油服股份有限公司,天津 300451;3中国船舶科学研究中心,江苏 无锡214082)
1 引 言
近年来随着电子计算机技术的飞速发展以及数值计算理论的不断成熟,计算流体动力学CFD方法凭借着其较高的计算精确度和相对低廉的费用,且能得到比模型试验更多的流场信息,正逐渐成为重要的船舶水动力性能分析手段。而SBD技术(Simulation Based Design)的形成[1],进一步发挥了CFD在工程设计优化中的作用,促使工程设计从传统经验设计模式向知识化设计模式的转变。该技术是将CFD技术和最优化技术全面融入船舶的设计进程,利用CFD对设定的优化目标(船舶水动力性能)进行数值计算,同时利用最优化技术和几何重构技术对船型设计空间进行探索,最终获得给定约束条件下的性能最优的船体外形,实现以性能驱动设计的目标。
本文基于iSight多学科优化平台,建立了一套基于CFD的船型优化系统。系统集成了船型变换及自动生成技术,通过对主要船型参数的控制,实现整个优化流程的自动化。利用iSight平台集成的多种优化算法及近似模型生成技术,可以自动实现从全局探索再到局部空间寻优的整个流程。基于该系统对一条设计船的阻力性能进行了优化,整个优化流程包括:对设计空间的初步探索、构建全局逼近响应面模型、利用遗传算法进行全局寻优并确定近似最优解、缩小设计空间并利用SQP算法进行局部寻优,直至逼近整体最优解。
2 基于母型改造的船型自动生成技术[2]
要对船型进行优化设计,就必须有一套灵活有效而又简便易行的方法来描述和修改船体的几何形状,用尽量少的设计变量来控制船型的生成,为阻力等学科的分析提供数值模型,实现优化过程的自动化。
2.1 船型变换系统介绍
在传统设计过程中,对船型的变化主要通过母型改造法来实现,该方式是行之有效的,但缺点是只能在主尺度参数相差不大的某一系列或母型船的基础上进行小范围的改变。本文所采用的船型生成系统,较之传统的母型改造方法有着更广的适用范围,通过对主要船型参数的控制,可以实现对母型船在较大尺度范围内的变化,同时又能很好地继承母型船线形上的特征,从而保证了新生成船型的优良性。
系统集成了样条曲线模块(SPLINE)、静水力计算模块(Hydrostatic)、仿射变换模块(STRETCH)、横剖面形状变换模块(CMVARY)和横剖面面积曲线改造模块(Lackenby)等,实现对主要设计变量包括排水体积(V)、船长(L),型宽(B),吃水(T),棱形系数(Cp)和舯剖面系数(Cm)等参数的控制。
通过样条曲线模块,将读入的母型离散型值点表达成连续的剖面曲线,利用仿射变换模块,将母型船变换到设计船要求的主尺度,在此基础之上,通过剖面变换模块,将母型船剖面系数变换到满足设计船剖面要求,之后,固定舯剖面形状,利用Lackenby模块对横剖面面积曲线进行改造,得到设计船要求的横剖面面积的纵向分布,即棱形系数值。系统中每一步计算模块的输入都是前一步计算模块的输出,通过这样一连串的改造,即可满足设计船要求的主尺度及船型参数要求。图1的框图表示了船型变换系统流程图。
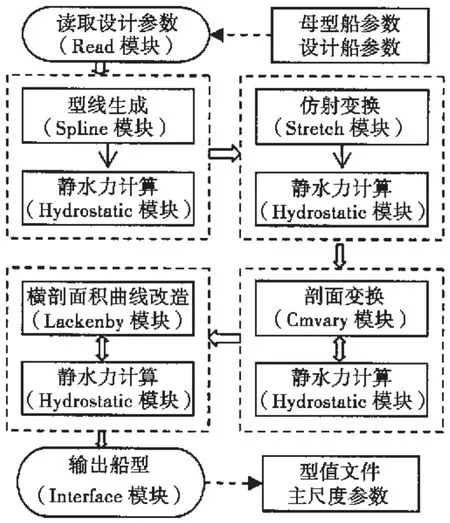
图1 船型变换系统流程图Fig.1 The overall process flow of hull transformation

图2 计算模型生成示意图Fig.2 Analytical model automatic generation system
阻力计算模型 接口模块
2.2 计算模型的自动生成
就船舶水动力性能而言,随着学科研究的深入,分析模型的精确度越来越高,功能也越来越强大,这些高精度分析模型可以为设计过程提供更多更可靠的信息。要利用这些分析工具,就必须为这些工具提供相应的计算模型,为此,船型自动生成系统提供了相应的数据接口模块,实现了船型变换系统与CFD分析软件之间的无缝连接。图2以阻力分析软件shipflow的计算模型生成为例,展示了计算模型的生成。通过该接口模块,可以将变换系统生成的新船型输出为shipflow可直接读取的数据文件格式,避免了人为地去修改文件格式以建立计算模型,使优化过程的自动化变得可行。
3 水动力(阻力)性能分析模型
3.1 基于CFD的阻力计算[3-4,10-11]
随着电子计算机技术的飞速发展以及数值计算理论的不断成熟,计算流体动力学CFD方法有了显著的进展,并逐渐用于生产实践。虽然限于当前的理论水平和计算机的运算速度,CFD方法离精确预报船舶的流体动力性能还有很大的差距。但是,CFD计算的结果仍然具有一定的工程精确度,它能获得比模型试验更多的流场信息,这在多方案优选和单目标优化中具有很大的意义,可以减少传统设计对模型试验的依赖。因此,如果能将CFD计算引入到实际船舶设计中去,通过结合具体船型进行CFD船舶快速性及流场特性预报,比较不同线型方案的快速性能优劣,这将对船舶设计起到很重要的推动作用。
迄今为止,基于势流理论的兴波阻力和绕船体波形的计算是CFD在实际船舶优化设计领域中应用最多的部分。一般采用面元法计算势流,自由表面一般采用线性或非线性边界条件。线性边界条件求解因为不需要将自由面的位置进行迭代,比较容易被没有CFD使用经验的用户使用;随着计算机技术的发展,已经能够通过数值计算方法直接求解各类控制方程和边界条件具有强烈非线性特征的大量流动现象,因而非线性方法较过去理论上更完善,计算结果更精确。
粘性流的计算是现在CFD的热点,因为绕船体粘性流的计算不仅可以预报模型或实船的粘性阻力,而且可以提供实船的有效伴流场分布、流场的分离以及后体丰满度的限制等信息,使得船型优化设计可以综合考虑阻力和尾部流场品质,在现今的粘性流计算方法中,RANS方法是主流。
国内外的研究者运用CFD手段针对船舶阻力性能的优化开展了大量的研究工作,研究对象从船体局部(球首等)到整体船型优化,数值计算方法由基于势流理论到粘性流计算,优化目标从单目标阻力最小,到综合考虑阻力、尾部流场品质等,体现了CFD技术在工程设计优化中所发挥的重要推动作用。
本文从减小船舶总阻力角度对设计船整体线形进行优化。总阻力成分中兴波阻力采用了基于Dawson二阶面元法的Shipflow势流求解模块进行计算;粘性阻力部分采用ITTC(1957)相关统计公式进行计算。
兴波阻力的计算通常有两种方法:一种是基于船体表面压力积分方法,另一种是基于自由表面波形积分方法。对于大多数CFD代码,常采用前一种方法计算船舶整体兴波阻力值,然而采用这种处理方式的话,对于那些反映波形阻力是如何增加或者减小的细节方面的信息我们将不得而知;此外,由于船体表面的复杂性,尤其是首尾部曲率变化较大或者存在折角的地方,计算网格容易存在缺陷,造成数值误差波动较大,结果易发散。考虑到设计船艉部线形较为复杂,采用表面压力积分方法计算结果的稳定性对船身网格划分依赖性较大,实际计算过程中经常出现发散的情况,如果人为地去修改网格也不利于整个优化过程的自动化。为了保证优化进程中数值计算的稳定性,本文中采用了基于自由表面波形积分的方法计算兴波阻力。
3.2 响应面近似模型技术[5]
随着船舶阻力学科计算理论的不断发展,相应的计算分析软件的功能也越来越强大,对计算机计算能力的要求也越来越苛刻,完成一次学科分析往往需要大量的计算时间,计算成本高昂,所以目前这些软件多作为学科分析工具,在船舶设计优化中并未充分发挥其作用,此外,由于有些问题的计算结果对输入参数很敏感,输入参数的微小变化就会引起输出量的很大扰动,产生数值噪声,造成优化进程易陷入错误的局部极值点而无法顺利完成。因而近似技术在优化设计和计算中得到了越来越多的研究及应用。
响应面近似方法是试验设计与数理统计相结合的一种综合应用,它是在试验测量、经验公式或数值分析的基础上,获取一组独立变量与系统响应之间某种近似关系的统计技术。它可以实现对设计空间的全局逼近,从而将复杂的学科分析从优化进程中分离出来,可以大大减少多学科优化设计问题的计算量,有效地解决整个优化进程中计算响应时长与计算精度之间的矛盾,此外,还可以平滑设计空间的数值噪声,防止数值优化方法陷入局部极值点。目前较为常用的全局近似方法主要有神经网络方法和多项式响应面方法。
构造响应面时,需要大量分布于设计空间的设计点,这些设计点称为实验设计点。如果设计点选择过多,则计算代价就较高,对于处理非线性响应问题更为突出,如何在选取较少设计点的同时又能够保证近似精度是响应面方法研究的焦点之一。一般采用试验设计方法来获取设计点,常用的有全因子试验法,正交设计法,重心复合设计法,拉丁方及优化拉丁方法等。

图3 计算试验点在设计空间的分布Fig.3 Scatter diagram of discrete numerical points
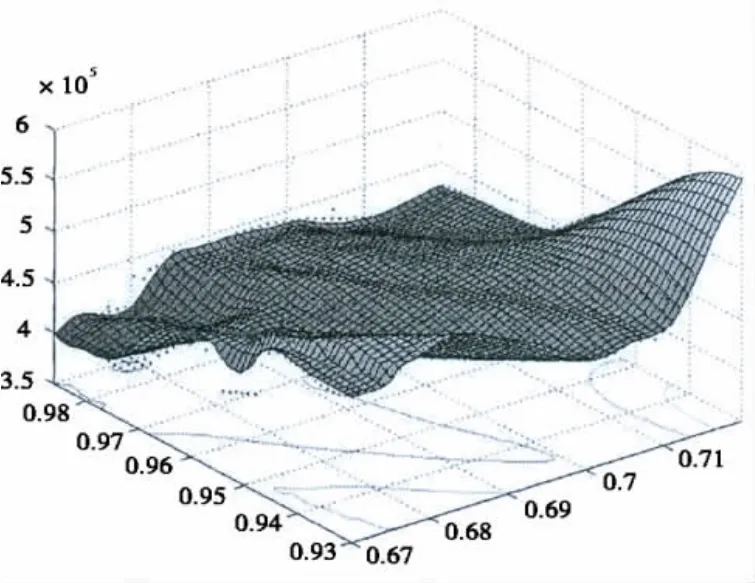
图4 基于神经网络的响应面模型Fig.4 Metamodel based on neural network
由于本文优化设计任务所选取的设计变量较少,因此我们采用全因子试验法在设计空间中均匀分布试验点,在对所有试验点进行详细计算后,利用生成的数据点构建合适的响应面模型。如图3所显示的是实际计算的试验点在设计空间的分布,图4所示是生成的基于神经网络的响应面模型。
4 优化系统的建立
4.1 任务集成
iSight软件是当前较为流行的实现设计优化过程的软件平台之一。它可以为设计者提供强大的过程集成功能,可以实现对已有商业软件和自编程序的集成,同时它还提供了多种常用的优化算法,具有强大的优化设计功能。
将船型变换系统和Shipflow软件集成到iSIGHT平台中,建立起如图5所示的任务进程。

图5 优化系统的集成Fig.5 Process integration of optimization system in iSight

图6 优化流程图Fig.6 Flow chart of hull optimization
图5中显示了任务中包含的执行模块,图6中框图则显示了优化系统的数据流,船型变换模块根据系统层优化器给定的设计变量生成新的船型,将计算模型传递给阻力计算模块,并输出相应的主尺度及船型参数文件,学科层分析模块通过调用Shipflow软件对给定的计算模型进行分析,完成后将结果反馈给系统优化器,即完成一次优化迭代。
4.2 组合优化策略[6-7]
由于该船肥短:LPP/B=4.06,船体表面曲率变化较大,造成了求解绕船体周围流场问题的复杂性,此外影响阻力性能的船型参数之间既相互关联又相互耦合,使得设计空间极不规则,具有高度的非线性特征。因此,一方面我们希望所选择的优化方法具有较强的全局搜索能力,避免陷入局部极值点,从而能够获得全局最优的设计方案;同时,由于求解问题的复杂性,不可避免地会造成学科分析的响应时间较长,因此我们又希望优化方法能够具有较强的局部搜索能力,迅速收敛到局部最优解。对于这样一个复杂的工程优化问题,单一的传统的优化算法很难获得满意的结果,而将多种优化方法的思想结合起来,逐渐形成的组合优化策略,对于高度复杂的优化问题的探索,具有较为突出的表现,它在寻优过程中可以充分发挥各单一优化算法各自的特点,通过先全局再局部,逐次逼近的思想,保证复杂工程问题最终收敛到全局最优方案。
本文采用了进化遗传算法(MIGA)与二次序列规划法(SQP)相结合的二阶组合优化方法,将响应面近似模型(RSM)引入到优化进程中,优化流程如图4所示。首先通过试验设计的方法生成设计变量与阻力性能的代理模型,利用遗传算法对基于响应面代理模型的整个设计空间进行探索,逐次迭代得到全局近似最优解后,缩小设计空间搜索范围,通过二次序列规划法在近似最优解附近进行局部寻优,直至逼近整体最优解。并将结果与直接数值优化的结果进行比较。
5 优化实例
本文选取的母型船主尺度及船型参数如表1所示,利用该系统对其线型进行优化,以实现阻力性能的最优。

表1 母型船主尺度参数Tab.1 Principal dimension and hull coefficient of Parent ship
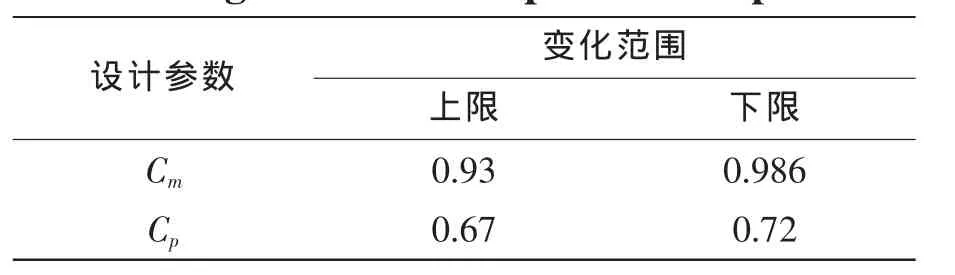
表2 设计变量及其取值范围Tab.2 Design variable of optimization problem
5.1 船型设计参数的选取
为了便于直观地比较线形变化对船舶总阻力的影响情况,同时考虑到保证母型船布置的特殊要求,优化实例中,我们令排水量和主尺度参数在优化过程中保持不变,仅通过改变船型参数来实现对型船线形的变换,通过调整设计吃水来补偿由于船型参数变化造成的排水体积的变化,设计变量及取值范围见表2所示。
5.2 优化问题的数学模型
优化目标:设计航速时的总阻力(Rt)最小。
优化变量:中剖面系数(Cm)、棱形系数(Cp)。
约束条件:(1)排水体积▽保持不变;
(2)除吃水外其他主尺度设计参数保持不变。
优化指标的计算:
将总阻力分为兴波阻力和粘性阻力两个部分,总阻力Rt=Rf(1+k ) +Rw。
(1)粘性阻力中,摩擦阻力系数采用ITTC(1957)公式计算;形状因子k采用下列公式计算:

相关变量的定义可以参考Holtrop阻力估算方法相关文献[8-9]。
(2)兴波阻力Rwp采用Shipflow软件计算得到。
优化算法选取:
优化算法选择MIGA与NLPQL相结合的组合优化算法。
5.3 优化过程及结果
整个优化历程分为两步,在第一步全局寻优阶段,共完成了12 027次优化,经过12次迭代后计算收敛,得到全局近似最优解,第二步局部寻优阶段,进一步缩小设计空间范围,将上一步得到的近似最优解作为局部寻优的初始设计点,在该点附近运用梯度算法进行寻优,直至逼近全局最优解,经过68次迭代后计算收敛,优化结束。优化迭代过程见图7。
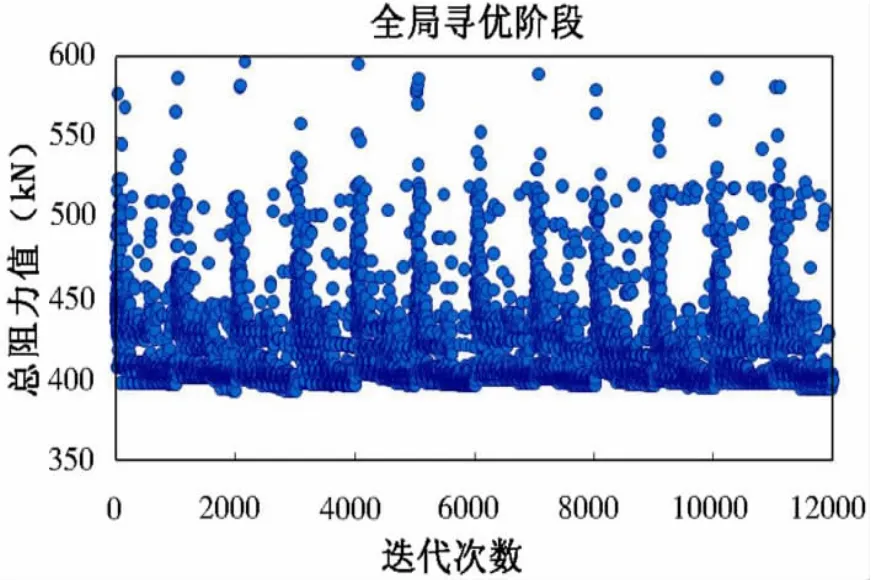
图7 (a) 全局优化迭代历程Fig.7(a)History plots of global optimization

图7 (b) 局部优化迭代历程Fig.7(b)History plots of local optimization

图8 母型船模型Fig.8 Figure of model test
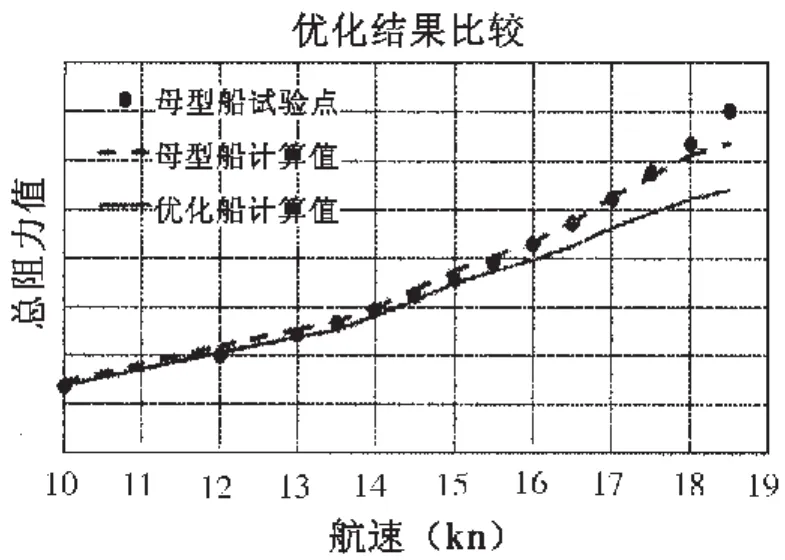
图9 优化前后阻力曲线比较Fig.9 Total resistance curve(ITTC based)of original and optimized

图10 优化前后剖面变化Fig.10 Section plan of original and optimized

图11 优化前后横剖面面积曲线变化Fig.11 Prismatic curve of original and optimized

图12 自由表面波形轮廓对比Fig.12 Wave contours of original(bottom)and optimized(top)
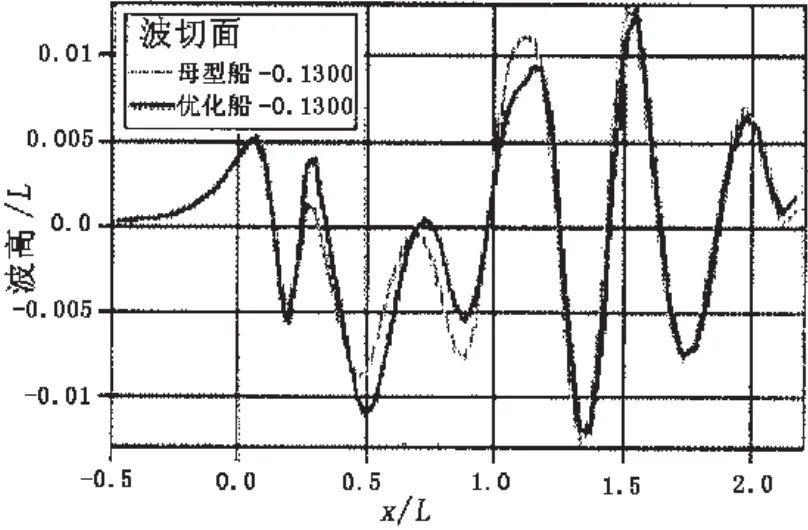
图13 舷侧纵切波形对比(at y/Lpp=0.13)Fig.13 Longitudinal wave cut at y/Lpp=0.13
图8是母型船的光体模型,在武汉理工大学拖曳水池完成其阻力试验,图9为阻力试验与数值预报结果的比较,证明了理论预报的可靠性,图9同时表示了优化前后阻力曲线的比较。图10、图11分别为优化前后船型横剖面曲线的变化以及横剖面面积曲线的变化;图12和图13分别为优化前后自由表面波形轮廓对比和舷侧纵切波形的对比。表3为优化结果汇总,在设计航速16kns时,优化后的船型总阻力减少了9.42%。

表3 优化结果汇总Tab.3 Optimization results
6 结 论
本文建立了一套基于CFD数值计算的船舶阻力优化系统,以船型变换及自动生成技术为核心,在此基础之上综合运用遗传算法、二次序列规划法和代理模型技术,通过一个算例来验证了系统的可行性。从数值优化结果来看,收到了预期的效果,在主尺度和排水量不变得前提下仅通过少量的改变船型系数设计变量参数,便实现了船舶阻力性能的提升。在接下来的研究中,我们还将针对优化的结果进行模型试验,以进一步来验证系统优化结果的可靠性。
[1]赵 锋,李胜忠等.基于CFD的船型优化设计研究进展综述[J].船舶力学,2010,14(7):812-821.Zhao Feng,Li Shenzhong,et al.An overview on the design optimization of ship hull based on CFD technigue[J].Journal of Ship Mechanics,2010,14(7):812-821.
[2]项久洋,毛筱菲.基于主要尺度要素的船型变换[J].中国舰船研究,2008,3(4):15-19.
[3]蔡荣泉.船舶计算流体力学的发展与应用[J].船舶,2002,8(4):8-13.
[4]Heimann,Justus.CFD based optimization of the wave-making characteristics of ship hulls[D].Dissertation TU Berlin,Mensch&Buch Verlag,ISBN 3-89820-445-6,2005.
[5]钟毅芳,陈柏鸿等.多学科综合优化原理与方法[M].第1版.武汉:华中科技大学出版社,2006.
[6]Koch P N,Evans J P,Powell D.Interdigitation for effective design space exploration using iSight[J].Structure and Multidisciplinary Optimization,2002,23(2):111-126.
[7]赖宇阳.叶片气动设计中组合优化方案的算法研究和系统实现[D].北京:清华大学,2002.
[8]Holtrop J,Mennen G.An approximate power prediction method[J].International Shipbuilding Progress,1982,29(335):166-170.
[9]Holtrop J.A statistical re-analysis of resistance and propulsion data[J].International Shipbuilding Progress,1984,31(363):272-276.
[10]Peri D,Rossetti M,Campana E F.Design optimization of ship hull via CFD techniques[J].Journal of Ship Research,2001,45(2):1-12.
[11]Peri D,Campana E F.Multidisciplinary Design Optimization of a naval surface combatant[J].Journal of Ship Research,2003,47(1):1-12.
