浅水中会遇船舶水动力相互作用数值研究
2012-06-07张晨曦邹早建
张晨曦 , 邹早建 ,b, 杨 勇
(上海交通大学a.船舶海洋与建筑工程学院;b.海洋工程国家重点实验室,上海 200240)
1 引 言
随着航运业的快速发展,港口、航道内的船舶密集程度越来越高,航行船舶与其他船舶的会遇、超越变得不可避免,过往船只对停泊的船舶产生的水动力干扰也不容忽略;另一方面,随着人类开发海洋步伐的加快,海上补给以及两船之间原油、天然气等货物的过驳输运等水上作业日益增加,也使船船之间或船舶与其它海洋结构物之间的水动力干扰问题呈现多样化。
邻近两船在靠近航行时,由水动力相互干扰产生的偏航力和力矩会很大程度上影响船舶的正常航行,严重的甚至会使船舶失去控制导致碰撞,造成海难事故。随着人们对于海上安全的关注程度不断提高,和船舶航行安全密切相关的船舶操纵性也日益得到重视。而船舶操纵性会受到上述各种情况下船舶与其他船舶或海洋结构物的水动力相互作用的不利影响,因此这些情况下的水动力干扰问题成为了当前的研究热点。不仅如此,随着现代船舶向大型化发展,相应发展较慢的港口、航道相对变窄、变浅,船舶经常需要靠近其他船舶航行,船舶之间的水动力干扰作用显著,带来了严峻的航行安全问题,也使研究船舶之间的水动力相互作用变得更加重要。
研究船舶之间的水动力相互作用通常可以采用模型试验方法和理论计算方法。国外学者很早就对两船水动力干扰问题进行了试验研究。采用模型试验方法,Newton[1]首先研究了深水中两船相互超越的问题,Müller[2]研究了两船在狭窄航道中的会遇与超越问题,Remery[3]给出了航行船舶对一系泊船舶的水动力影响,Dand[4]研究了沿两平行航线会遇与超越的两船之间的相互作用。近年来,Vantorre[5]通过约束模试验全面研究了各种情况下的两船水动力相互作用。
在理论计算方面,两船非定常水动力干扰问题的研究大多采用势流方法。Tuck和Newman[6]、Yeung[7]、Kijima[8]、Tim[9]等人利用基于细长体理论的匹配渐进展开法分别对开阔水域浅水和深水中两船之间水动力相互作用、浅窄航道中两船之间水动力相互作用以及两船水动力相互干扰下的下沉与纵倾进行了研究;郑才土[10]利用奇点叠加法对浅窄航道中的两船水动力相互干扰进行了研究;张谢东等人[11-12]利用边界元方法研究了浅水中两船超越和会遇的情况;陈波和吴建康[13]利用Green-Naghdi方程,考虑波浪影响研究了两船交错运行的波浪干涉作用。近年来,随着CFD技术的不断发展,对于船舶相互作用的研究也逐渐转向粘性流方向。Chen等人[14]利用浸入边界法,通过求解RANS方程,考虑风和岸壁的影响研究了浅水中两船和多船水动力相互干扰问题。
本文应用FLUENT软件,采用动网格及滑动交界面技术,对两船在浅水中会遇的三维非定常粘性流场进行了数值模拟,计算了船-船水动力相互作用。通过将计算得到的水动力与试验数据对比,验证了本文方法的有效性。进而,通过对比整个会遇过程中船-船水动力相互作用随船舶横向间距、水深、船速以及船长的变化规律,分析了这些因素对两船之间水动力相互作用的影响。本文研究结果对于指导浅水航道中的船舶安全操纵具有一定的参考价值。
2 数学模型
2.1 坐标系

图1 坐标系Fig.1 Coordinate systems
考虑两船在浅水中分别以定常航速U1和U2沿平行直线相向而行的会遇情况,如图1所示。两船(Ship1和Ship2)的横向间距为Sp,纵向间距为ST,水深为h。作用在Ship1上的横向力和首摇力矩分别为F1和M1,作用在Ship2上的横向力和首摇力矩分别为F2和M2。采用三个右手直角坐标系:空间固定坐标系o-xyz、固定在Ship1上并以U1运动的运动坐标系o1-x1y1z1和固定在Ship2上并以U2运动的运动坐标系o2-x2y2z2,其中xoy平面、x1o1y1平面和x2o2y2平面均位于无扰自由面上。在运动初始时刻,空间固定坐标系的原点位于(ST0/2,Sp/2,0),ST0为初始纵向间距。
2.2 控制方程
由于两船在会遇状态下的船速相对于正常航行状态下的船速较低,因此本文忽略兴波的影响,对自由面使用刚性自由面假定,整个流场属于单相、三维、粘性和非定常的不可压缩流体流动。对湍流的模拟采用雷诺平均方法,在空间固定坐标系下,控制方程为如下连续性方程和动量方程:

式中,xi为坐标分量,ρ为流体质量密度,ui为平均速度分量,p为流体平均压力,为雷诺应力项。
综合考虑计算精度和计算时间,本文选择RNG k-ε两方程湍流模型进行计算。RNG k-ε湍流模型的湍流动能k及湍流耗散率ε方程如下:

式中Gk为平均速度梯度引起的湍流动能产生项,表达式为:

其中μt为湍流粘度系数,其他项的表达式以及常数为:

3 数值方法
3.1 边界条件及网格划分
本文研究的是浅水中两船会遇问题,前后左右流域范围应设置得足够大以消除边界对流场的影响。计算中设定船体表面和水底面为无滑移壁面边界。由于本文采用的是固定坐标系且考虑的是静水中的两船会遇问题,所以,对于流域左右两侧的边界,取其距离船体足够远,可以认为对流场不产生干扰,因此也设置为无滑移壁面边界;对于流域前后的边界,将其取在距离船体前后足够远的地方,流动充分发展,因而在其上设定压力出口边界条件。同时,考虑到刚性自由面假定,将自由面(即计算域上表面)设置为对称边界。经数值比较验证,本文计算流域取左右宽度为2.6倍船长,前后长度为8倍船长的范围;两船初始位置以区域中心点等距离放置。边界条件的设定如图2所示。

图2 边界条件Fig.2 Boundary condition
船体周围采用四面体网格与六面体网格的混合网格:在船体首部和中部采用六面体网格;在船体尾部几何比较复杂的部分采用适应性强的四面体网格,同时也便于控制动网格区域中网格的数量;在其余区域采用六面体网格。
3.2 动网格方法
动网格方法适合用来模拟流场形状由于边界运动而随时间改变的问题,包括预定义的运动和事先未知的运动。对于动网格,FLUENT提供了三种网格更新方法:弹簧光顺模型(Spring Smoothing),局部重划模型(Local Remeshing)以及动态层模型(Layering)。结合本文所考虑的问题,船体沿固定直线单自由度运动,在动网格区域中船体前后使用的是六面体网格,适合采用动态层模型来进行网格更新。动态层模型的基本原理为根据运动网格在相邻边界处的高度变化来对边界处网格层进行分割或合并,如图3所示。

图3 动态层模型示意图Fig.3 Sketch of layering
第j层网格作扩大变化时,如果其高度的最大值 δmax大于临界值 (1+ αs)δ0,则根据设定将其划分为两层;第j层网格作缩小变化时,如果其高度的最小值δmin小于临界值αcδ0,则将其与上一层网格合并。在此δ0为理想网格单元高度,αs,αc分别为分割因子与合并因子。同时,为了保证计算的稳定和精度,本文船体周围的网格保持不变,而在前后两端采用顶部铺层的动态层模型。
由于两船只是沿固定直线作相对运动,因此只需在流域中分别以两船航行的直线为中心,将宽度稍宽于船体的区域设定为动网格区域,如图2所示。动网格区域内的网格随船体整体移动,在船体前后的流域边界处进行分割与合并;其他区域为静止区域,动网格区域与静止区域之间采用滑动网格交界面技术进行数据交换。
3.3 UDF的使用
本文使用用户自定义函数(UDF),通过调用FLUENT自带的DEFINE宏实现以下目标:
(1)对两船的速度进行设定;
(2)考虑到随着船体的移动,力矩中心也随之移动,以计算时间和船速为参数设定力矩中心的位置;
(3)调用FLUENT自带函数对每一时间步中船体表面所受的力与力矩进行计算;
(4)将所计算的结果写入文件以便进行分析处理。
3.4 数值求解方法
本文采用FLUENT软件,以有限体积法离散流体运动的控制方程和湍流方程,其中扩散项采用中心差分格式,对流项、湍流动能方程以及湍流耗散率方程采用二阶迎风差分格式,速度、压力的耦合迭代采用SIMPLEC算法。
4 方法的验证与计算结果影响因素的分析
4.1 方法验证与计算结果分析
由于缺乏试验船型数据,本文计算所用船型为和试验船型相近的船型。计算及试验所用的两艘船的船型有关参数见表1(其中*为用于水动力相互作用比较验证的船型)。表1中,L、B和D分别为船长、船宽和吃水;CB为方形系数,λ为缩尺比。

表1 计算及试验所用船型主要参数Tab.1 Main parameters of ships used in calculation and experiment
本文在模型尺度下进行了计算,计算中两船模航速相等,其傅汝德数分别为0.086 6和0.085 3;计算工况满足实船和船模的傅汝德数相等。
为了便于比较,计算结果表达成无因次的形式。作用于船上的横向力、首摇力矩以及纵向距离的无因次表达为:

式中,F,M分别为横向力与首摇力矩,U为船速;船间纵向距离ST在会遇前定义为负值;下标1和2分别表示Ship1和Ship2。
图4和图5给出了计算得到的船舶所受横向力和首摇力矩与试验结果的对比。从图中可以看出,计算结果与试验结果吻合较好。
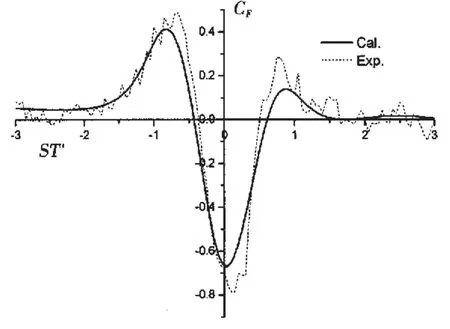
图4 横向力系数计算值与实验值的比较Fig.4 Comparison of sway force coefficient between numerical and experimental results

图5 首摇力矩系数计算值与实验值的比较Fig.5 Comparison of yaw moment coefficient between numerical and experimental results
如图4所示,横向力的受干扰范围大致为ST′=-2~2,并且其变化经历了三次极值:在ST′=-2~-0.8处为正,并不断增加;在船首刚刚交会后(ST′≈-0.83)达到极值并迅速减小,于ST′≈-0.43处过零后直至两船船舯纵向位置重合附近(ST′=0)达到负的最大值,其幅值为前一次极值的1.6倍以上;后半段基本上是一个对称的过程,但从相位上看稍有推迟,从负的极值上升到ST′≈0.6处改变方向,在ST′≈0.9附近达到正的第三个极值,但幅值只有第一个极值的1/4;之后随着继续航行,横向力趋向于零。从图5可以看出,首摇力矩的变化比较复杂,受干扰范围大致也为ST′=-2~2,有四次极值,其中第一次极值的幅值明显大于其他三次:在ST′=-2~-0.9的范围内,力矩为正,并不断增加至ST′=-0.9处到达极值后迅速下降,在ST′≈-0.45处转变方向并于ST′≈-0.23处达到负的第二个极值;随着两船进一步接近,首摇力矩增加至ST′≈0.33时达到正的第三个极值,之后又继续下降,在ST′≈0.9处达到负的第四个极值;最后随着两船距离的增加趋于零。与横向力的变化对比,首摇力矩的第一个极值发生在横向力第一个极值附近,第二个极值与横向力第一个过零点基本同步,之后第三个极值稍早于横向力第二个过零点,最后一个极值与横向力第三个极值基本同时出现。
结合横向力和首摇力矩的变化曲线来看,ST′=-1~1范围是两船会遇过程中的危险区间:首先,在此范围前段(ST′=-1~-0.5),船舶所受横向力和首摇力矩都处在第一个极值点附近,极易出现船舶本身的控制力不足以抵消干扰力的情况而造成失控。之后在ST′=-0.5~0的过程中横向力迅速下降,力矩也达到了负的第二个极值(ST′≈-0.23),此时横向吸引力虽然没有达到最大值,但也已经超过极值的一半,因此非常容易引起船舶的相互吸引而导致船首碰撞;在后半段,在吸引力还没有完全消失的时候,力矩又达到了正的第三个极值(ST′≈0.3),这时对应两船船体后部相对的状态,容易发生船尾的相互碰撞。

图6 ST′=-1.673时的无扰自由面上压力分布Fig.6 Pressure on the undisturbed free surface at ST′=-1.673

图7 ST′=-0.827时的无扰自由面上压力分布Fig.7 Pressure on the undisturbed free surface at ST′=-0.827

图8 ST′=0.019时的无扰自由面上压力分布Fig.8 Pressure on the undisturbed free surface at ST′=0.019

图9 ST′=0.865时的无扰自由面上压力分布Fig.9 Pressure on the undisturbed free surface at ST′=0.865

图10 ST′=1.711时的无扰自由面上压力分布Fig.10 Pressure on the undisturbed free surface at ST′=1.711

图11 ST′=2.557时的无扰自由面上压力分布Fig.11 Pressure on the undisturbed free surface at ST′=2.557
图6至图11给出了不同时刻无扰自由面上的压力分布图,其中颜色越深表示该区域压力值越小。从图中可以看出,随着两船的接近,船体两侧的压力差也不断变化。按照前进方向,船体在接近过程中右侧压力先是逐渐变大,此时横向力为正并经历第一次极值;接下来随着两船纵向距离的进一步减小,右侧压力迅速减小并远低于左侧压力,在两船平行时达到吸引力的极值;之后,右侧压力逐渐增加并再次超过左侧压力,出现第三个极值,最后两侧压力随着两船距离的增加而趋于平衡。
4.2 船间水动力干扰的影响因素分析
在此就两船横向间距、水深、两船相对速度以及船长的变化对浅水中会遇船舶船间水动力干扰的影响进行分析。这里使用两艘相同的KCS船进行计算,只给出Ship1的受力计算结果。表2给出了计算工况。

表2 不同参数的计算工况Tab.2 Conditions of parameter variation
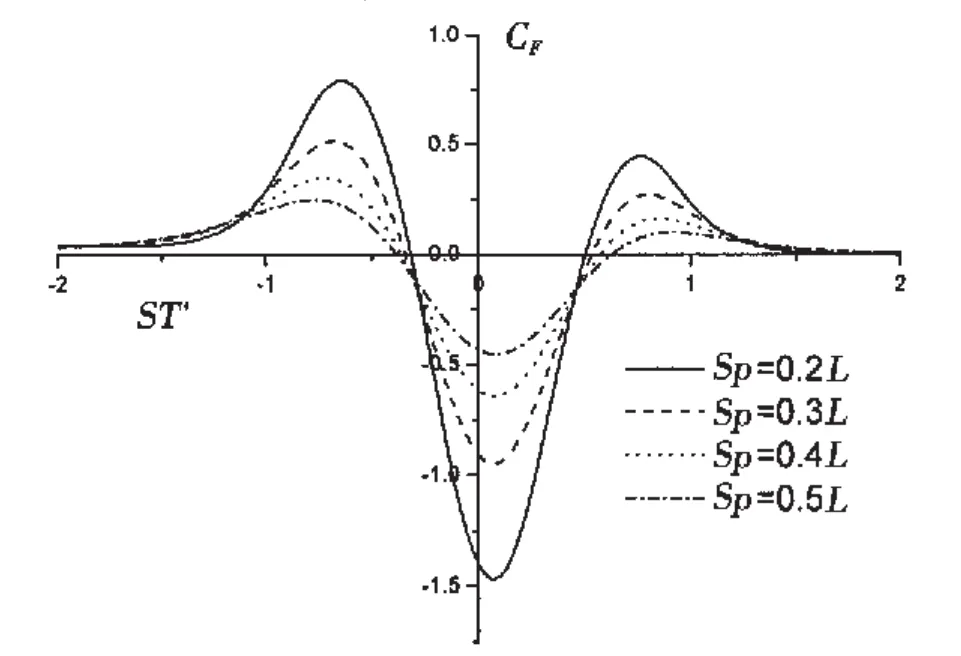
图12 不同横向间距下的横向力系数Fig.12 Sway force coefficient at different Sp

图13 不同横向间距下的首摇力矩系数Fig.13 Yaw moment coefficient at different Sp
图12和图13给出了不同横向间距下的船舶所受横向力和首摇力矩系数曲线。从图中可以看出,横向间距的减小对横向力和首摇力矩的每个极值都起到了放大作用,而且距离越小放大作用越明显。从相位上看,横向力的第一个极值和第三个极值的出现时刻随着横向间距的减小分别推迟和提前,第二个横向力的极值出现的时刻基本相同。首摇力矩的相位变化也有相同的规律,中间的两个较小的极值的相位基本不变,而前后两个极值的出现分别随着横向间距的减小而推迟和提前。图14和图15给出了不同水深情况下的船舶横向力和首摇力矩系数曲线。从图中可以看出,与横向间距的变化类似,水深的减小对于两船的水动力干扰同样起到了放大作用,而且水越浅,放大作用也越明显。由图15可知,水深对首摇力矩的第一个极值和最后一个极值的幅值的影响比较明显,对于中间两个极值附近范围的影响相对较小。从极值出现的时刻看,水深的影响与横向间距的影响稍有不同:就横向力而言,不同水深对于各个极值出现的时刻基本没有影响;就首摇力矩而言,水深的变化只对第二、三次极值出现时刻有些影响,对于其他两次极值的影响较小。
图16和图17给出了船速比的变化对两船水动力干扰的影响。从图中可以看出,随着Ship2船速的增加,Ship1船的受力会被明显放大,而且速度越快,放大作用越明显。从极值出现的时刻看:随着船速的增加,Ship1所受横向力的第二次极值出现的时刻不变,前后两个极值出现的时刻分别稍有提前和推迟;首摇力矩的前两个极值和后两个极值的出现时刻随着速度的增加分别提前和推迟。

图14 不同水深下的横向力系数Fig.14 Sway force coefficient at different h/D

图15 不同水深下的首摇力矩系数Fig.15 Yaw moment coefficient at different h/D

图16 不同船速比下的横向力系数Fig.16 Sway force coefficient at different U2/U1

图17 不同船速比下的首摇力矩系数Fig.17 Yaw moment coefficient at different U2/U1
图18和图19给出了船长比的变化对船间干扰力的影响。这里的工况是保持Ship1的船长不变,按照比例缩放Ship2的大小。从横向力的对比图可见,随着Ship2船长的增加,Ship1所受横向力在各时刻的绝对值也变大,各曲线交点在过零点附近;由首摇力矩的对比图可知,除了在第三个极值附近各曲线几乎重合以外,Ship2船长的增加对于其他三个极值都起到了不同程度的放大作用,其中第一个极值放大最明显,其次是第四个极值。船长的变化总体来说对横向力和首摇力矩极值的出现时刻影响较小。

图18 不同船长比下的横向力系数Fig.18 Sway force coefficient at different L1/L2

图19 不同船长比下的首摇力矩系数Fig.19 Yaw moment coefficient at different L1/L2
5 结 论
本文针对浅水中两船会遇问题,采用CFD软件FLUENT,选取RNG k-ε湍流模型,对非定常RANS方程进行求解,应用UDF和动网格技术,在刚性自由面的假定下进行了粘性流场数值模拟和船间水动力相互作用计算。主要结论如下:
(1)通过将计算结果与试验结果进行对比,验证了本文方法能够较好地应用于计算两船会遇状态下的水动力相互作用。
(2)对会遇过程中横向力和首摇力矩变化情况的分析表明,ST′=-1~1为两船会遇过程中的容易失控和发生碰撞的阶段。
(3)分别对比浅水中两船会遇情况下的横向力和首摇力矩计算结果随船间横向间距、水深、船速及船长的变化规律,表明这四种因素对于船舶会遇情况下的水动力相互作用都有着重要的影响。
本文方法及研究结果可以为研究复杂的船间水动力干扰问题提供参考,为浅水航道中船舶安全操纵提供理论依据。
[1]Newton R N.Some notes on interaction effects between ships close aboard in deep water[C]//First Symposium on Naval Maneuverability.Washington DC,1960:1-24.
[2]Müller E.Untersuchungen über die gegenseitige Kursbeeinflussung von Schiffen auf Binnenwasserstrassen[J].Schiff und Hafen,1967,19(6):393-406.
[3]Remery G F M.Mooring forces induced by passing ships[C]//Offshore Technology Conference.Dallas,1974,Paper No.2066,1974.
[4]Dand I W.Some measurements of interaction between ship models passing on parallel courses[R].National Maritime Institute,1981,Report R 108.
[5]Marc Vantorre,Erik Larforce,Ellada Verzhbitskaya.Model test based formulations of ship-ship interaction forces for simulation purposes[C]//IMSF-28th Annual General Meeting.Genova,Italy,2001.
[6]Tuck E O,Newman J N.Hydrodynamic interactions between ships[C]//10th ONR Symposium on Naval Hydrodynamics.Cambridge,Mass.USA,1974:35-70.
[7]Yeung R W.On the interactions of slender ships in shallow water[J].Journal of Fluid Mechanics,1978,85:143-159.
[8]Kijima K.Manoeuvrability of ships in confined water[C]//International Conference of Ship Manoeuvrability.London,1987,Paper No.20,1987.
[9]Gourlay T.Sinkage and trim of two ships passing each other on parallel courses[J].Ocean Engineering,2009,36:1119-1127.
[10]郑才土.浅水中船舶相互作用的一种计算方法[J].船舶工程,1994(6):8-14.
[11]张谢东,刘祖源,吴秀恒.船舶超越时相互作用力理论计算[J].武汉交通科技大学学报,1997,21(3):236-241.
[12]Zhang Xiedong,Wu Xiuheng.Study of hydrodynamic forces of ships in narrow waterway[J].Journal of Hydrodynamics,Ser.B,2003,4:113-117.
[13]陈 波,吴建康.浅水域中两船交错运行时的非定常波浪干涉[J].水动力学研究与进展,A辑,2005,20(4):486-491.
[14]Chen H C,Liu T,Huang E T.Application of chimera RANS method for multiple-ship interactions in a navigation channel[C]//Proceedings of the Twelfth International Offshore and Polar Engineering Conference.Kitakyushu,Japan,2002:26-31.
