基于Volterra自适应滤波器的发动机运转噪声预测

张 立，石要武，马 彦

(1.吉林大学 珠海学院，广东 珠海 519041;2.吉林大学 通信学院，长春130022)

发动机在正常工作时，由于机械运动部件之间相互冲击碰撞、进排气流运动、燃料燃烧及高压电磁交互作用等原因，会发出很大的噪声。当出现运动部件磨损、配合间隙增大、零件松动、断裂损坏等现象时，或者由于维修质量不好、装配调整不当等原因，发动机运转噪声中会伴随着产生各种异常声响。因此，基于发动机异响信号分析的故障诊断研究得到了广泛关注和经验性实际运用［1］。许多研究工作采用小波/小波包分析、模糊理论、人工神经网络、谱相关分析、循环统计量分析和时频分析等方法直接对发动机异响信号进行建模、特征提取及模式识别［2－11］。由于采集到的声响是含有发动机运转噪声的混合信号，且通常信噪比低，将不可避免地导致较高的故障虚报、漏报概率，故障分辨率较低，鲁棒性也较差。因此，对发动机运转噪声进行预测，对于减小发动机运转噪声干扰、提高异响信号信噪比、提高基于异响信号分析的发动机故障诊断的正确率具有重要意义。

自适应噪声对消法是从混合信号中增强或提取感兴趣信号的经典方法［12－13］，对消效果主要取决于噪声预测的精度，而噪声预测的精度则主要取决于自适应滤波器参考输入噪声与期望输出(实测噪声)的相关程度、相互间的泛化表达能力及自适应调节速度及精度。

发动机是一种包含循环往复直线运动、旋转运动及多种伴生的周期性物理化学动力学过程的复杂机械系统;此外，发动机的运动状态受众多因素影响，且许多因素是不可控的或虽可控但无法精确控制;再加上人工操控的模糊性及随机性的影响，发动机的运转即使是在恒转速操控工况下也是不稳定的。所以，发动机运转噪声呈现出明显的非线性动力学特性、准周期特性及一定的随机性。上述特性为发动机运转噪声的建模和预测带来一定的困难，但也提供了新的途径。

基于归一化 LMS(NLMS)Volterra自适应滤波器［14－15］，本文提出两种发动机恒转速操控工况下的运转噪声预测方法，有效地利用了Volterra级数强大的非线性映射能力。其中，基于模板噪声的发动机运转噪声预测方法，还充分考虑了发动机运转噪声内在的相关性、周期性及随机性，可仅利用单传感器实现较高精度的噪声预测，为发动机故障异响侦测及后续的故障诊断提供必要的基础。

1 Volterra自适应滤波器

1.1 基于一维时间序列的相空间重构

Packard等［16］提出通过对原始一维观测时间序列的时间延迟来重构动力学系统的相空间。Takens［17］证明，如果嵌入维数dE≥2D+1(D为动力系统的实际维数)，则重构相空间流形与原系统流形微分同胚。这从理论上证明了，对于一具有确定性动力学机制、影响因素众多但难以直接监测的系统，可通过对其单一变量进行观测而获得对其内在动力学特性的估计，并可据此对观测时间序列进行短期预测。

设观测时间序列为发动机运转噪声，标记为{x(m)，m=1，2，…}。通过时间延迟，将其嵌入到 dE维相空间中，对应的相空间中某状态点坐标为X(m)=［x(m)，x(m － τ)，…，x(m －(dE－1)τ］T。

1.2 基于三阶Volterra级数及NLMS算法的自适应滤波器

用Volterra级数展开式作为Volterra滤波器预测发动机运转噪声的表达式为:

其中:hp(m1，m2，…，mp)为 p阶 Volterra核。考虑到实际系统的有限记忆性、Takens定理关于嵌入维数dE≥2D+1的结论、实际系统非线性耦合程度以及数值逼近过程中的舍入误差等因素，上式一般取有限阶截断及有限次求和形式。对于发动机运转噪声信号，经试验验证，三阶Volterra级数可在逼近精度和计算复杂度之间取得较好折衷，即:

一般记忆深度取为P=dE。

定义三阶Volterra滤波器的非线性扩展输入向量及滤波器各阶核组成的权向量分别为:

则式(3)可重写为:

定义滤波器预测误差为:

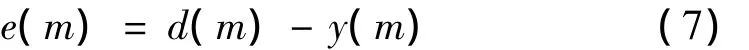
采用归一化LMS(NLMS)自适应策略对Volterra核进行自适应修正，滤波器权系数更新公式为［10］:

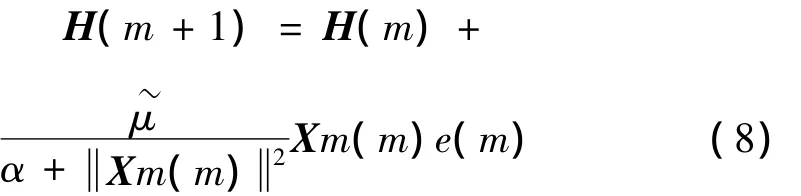
由Volterra滤波器及NLMS自适应策略构成的Volterra自适应滤波器可实现对非平稳的发动机运转噪声的跟踪和预测。

1.3 NLMS自适应算法性能改进

标准NLMS的一个明显不足是对于相关性较强的信号，滤波器权值在失配状态下调整速度慢，导致算法的收敛速度慢、失调误差较大。采用NLMS算法的三阶Volterra自适应滤波器，其扩展输入向量中包含滤波器抽头输入向量的高阶矩，其前后时刻的相关性更强。因此，收敛速率更低，严重影响预测精度。已有研究表明，滤波器权值调整量的大小取决于输入向量Xm(m)与Xm(m－1)的相关系数ρ(m)，且当该相关系数为0、即Xm(m)与Xm(m－1)正交时，滤波器的收敛速率最快［12］。为此，引入新向量［18］:

其含义为当前时刻输入向量与前一时刻输入向量不相关的部分，其中，相关系数ρ(m)定义为:

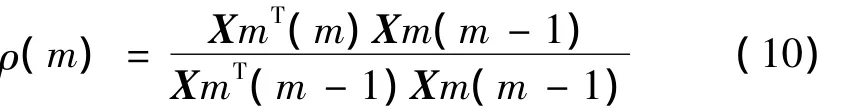
由于

可知，U(m)与m－1时刻的输入Xm(m－1)是正交的。因此可将U(m)作为滤波器输入向量，得到滤波器权系数更新公式为:

本文以下称这种改进的滤波器为去相关NLMS Volterra自适应滤波器。

2 发动机运转噪声的预测

着眼于发动机运转噪声的自适应抵消应用，提出以下两个自适应噪声抵消方案。

2.1 基于强相关通道同步观测时间序列的发动机运转噪声预测

预测方法如图1所示。由于两个传感器通道采集的发动机运转噪声为同步采样获得，所以相关性较强，则滤波器动态响应速度就成为影响预测精度的关键因素。

图1 基于强相关通道同步观测时间序列的信号预测Fig.1 Signal prediction scheme based on another strongly correlated time series observed by synchronized sampling

2.2 基于模板噪声的发动机运转噪声预测

由发动机工作原理可知，发动机运转噪声是由其内部直线循环往复、旋转等周期运动过程中各种物理化学作用所衍生的，具有明显的周期特性。因此，不同工作循环过程中发出的运转噪声之间具有很强的相关性。这启发我们，可以将没有故障异响时的“纯净”的发动机运转噪声序列作为先验知识，制成模板噪声，作为Volterra自适应滤波器的参考输入，利用其与现场实测发动机运转噪声之间内在的相关性，通过Volterra自适应滤波器来表达和预测实测噪声信号，方法如图2所示。该方法只需一个传感器。

图2 基于模板噪声的信号预测Fig.2 Signal prediction scheme based on template noise

由于虚拟参考通道中的模板噪声与主通道实时采集到的噪声信号是非同步采样方式获得的，两个通道时间序列不同时间窗口内数据向量的相关性有较大差异。显然，曲轴转柄机构位于相同相位时的噪声具有更强的相关性。因此，为提高预测精度，需对两个通道的信号进行相位同步处理。具体处理流程如下。

(1)N阶中值滤波

为了提取与发动机活塞循环往复直线运动及曲柄连杆机构旋转运动相对应的噪声信号的周期和相位信息，通常采用低通数字滤波方法。但是，低通滤波器会造成信号相位的滞后，因此，直接采用N阶中值滤波。经试验优选，对处于怠速至2 500 r/min转速范围内的发动机运转噪声来说，滤波器阶数N一般选择在400左右比较合适。如图3所示。

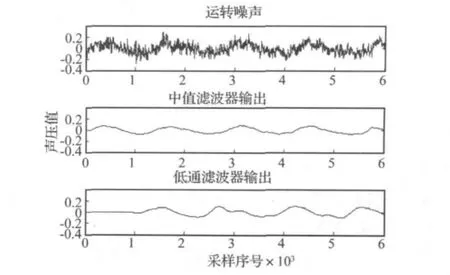
图3 低通数字滤波器与中值滤波器输出的相位信息Fig.3 Phase information exhibited from the output of a low pass filter and the output of a median filter

(2)通过Hilbert变换提取相位、周期信息

对中值滤波后的发动机运转噪声进行Hilbert变换，得到滤波后信号的相位信息，如图4所示。通过搜索和标注相位由+π到－π的跳变点即可得到各个周期的起止点。

图4 Hilbert变换后提取的发动机运转噪声的相位信息Fig.4 Phase information of engine running noise extracted by Hilbert transformation

(3)参考通道模板与主通道期望响应的相位同步

将无故障时“纯净”的发动机运转噪声经上述步骤处理后，截取其中一个周期的片段作为噪声模板。将待跟踪预测的噪声信号也经上述步骤进行处理。预测开始时，两路信号按相位进行匹配、同步，噪声模板循环使用，直至期望信号结束。

3 发动机运转噪声预测试验及结果分析

采用NI Labview 2009专业版环境下的数据采集助手NI－DAQmx、BSWA TECH公司的声压传感器MPA416(2路)及美国NI公司的9234数据采集模块(具有4个实时并行模入通道)构成数据采集系统。试验中采样频率为Fs=44 100 Hz。采集到的发动机运转噪声数据(声压值)统一标准化为.wav格式。此外，试验中使用的4缸EFI发动机型号为CAF483Q0，试验前发动机预热至标准工作温度。

预测误差采用均方误差MSE(误差能量平均值)、相对误差PERR(误差能量与信号能量之比)来度量:

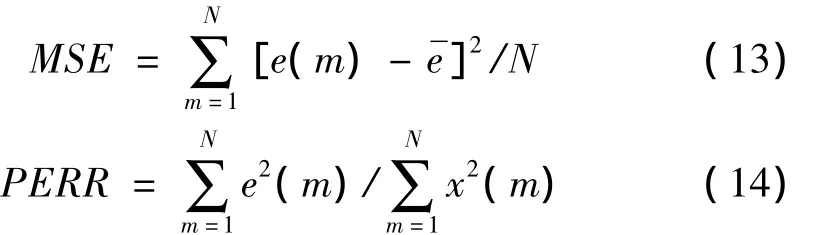
其中:N为信号预测长度。

3.1 基于强相关通道同步观测时间序列的发动机运转噪声预测试验

采用上述数据采集系统对四种转速1 000 r/min、1 500 r/min、2 000 r/min及2 500 r/min下的发动机运转噪声的声压值进行双通道数据采集。数据采集过程中两传感器与发动机大致等距，相互间距为30 cm。以平均预测误差最小为目标进行试验优选，确定嵌入相空间及NLMS自适应Volterra滤波器(VAF)参数如下:延迟时间τ=1、嵌入维数dE=4、滤波器步长因子~μ=1.4、α =0.001、P=4，所有滤波器权系数初始值固定设为零。

随机选取1 000 r/min工况下的一个运转噪声样本对标准NLMS自适应线性滤波器(LAF)、标准NLMS自适应Volterra滤波器及去相关NLMS自适应Volterra滤波器的学习速率进行了对比试验。图5中显示的是滤波器第1个权值迭代修正的过程曲线。

图5 三种自适应滤波器的发动机运转噪声学习曲线Fig.5 Engine running noise learning processes of three adaptive filters

由图5可见，标准NLMS线性自适应滤波器及标准NLMS Volterra自适应滤波器的学习速率几乎相同，但二者均远远低于去相关NLMS Volterra自适应滤波器的学习速率。以权系数由0逐步修正更新至5来说明，前两者差不多需要26 000次迭代，而去相关NLMS Volterra自适应滤波器仅需要大约2 600次迭代即可稳定达到，较前两者速度提高约10倍。

根据图1所示系统结构，分别采用几种自适应滤波器，在经充分训练(50 000次)后，对4种转速下的发动机运转噪声序列片段进行了16组Monte Carlo仿真预测试验。考虑到计算机内存及计算时间开销，每组仿真试验各做30次，每次从相同转速下的30组不同的发动机运转噪声样本(20 000点，0.45 s)中随机选取1个进行试验。结果示于表1、表2中。其中，混合NLMS VAF方法是指采用去相关NLMS算法训练Volterra滤波器各阶权系数，然后采用标准NLMS算法实时更新Volterra滤波器权系数来进行跟踪预测。

表1 充分训练(50 000次)后的稳态预测误差(MSE)Tab.1 Steady state prediction error(MSE)of 4 adaptive filters after being fully trained(50 000 times)

表2 充分训练(50 000次)后的稳态预测误差(PERR)Tab.2 Steady state prediction error(PERR)of 4 adaptive filters after being fully trained(50 000 times)

由表可见，不管采用何种权系数修正策略，Volterra自适应滤波器的预测精度均高于标准的线性自适应滤波器，说明对于发动机运转噪声，Volterra自适应滤波器具有更强的泛化表达能力。另外，去相关NLMS算法虽可大幅提高权系数的收敛速率，但在滤波器处于相对稳定响应状态下，标准NLMS算法具有更小的稳态失调误差。

3.2 基于模板噪声的发动机运转噪声预测试验

采用前述数据采集系统对 1 000 r/min、1 500 r/min、2 000 r/min转速下发动机运转噪声的声压值进行单通道数据采集，然后根据图2所示系统结构进行Monte Carlo噪声预测仿真试验。同样，以平均预测误差最小为目标进行试验优选，确定嵌入相空间及NLMS自适应Volterra滤波器参数如下:延迟时间τ=1、嵌入维数dE=18、滤波器步长因子~μ=1.4、α=0.001、滤波器抽头数P=18。相较于图1所示的试验方案，滤波器抽头数大幅增加。这是因为，此方案中，模板噪声与实测噪声为非同步采样所得，对应的发动机工况也难以保持一致，因此，两信号具有相关关系的数据窗口的大小及时序相对位置存在一定的随机性。为加大模板噪声与待预测噪声的相关性，自然需要加大滤波器抽头数。

从1 000 r/min转速下发动机运转噪声的历史记录中抽取出一段(10 000点)作为模板噪声。采用模板噪声对滤波器进行训练(20 000次)后，对1 000 r/min转速下的30个发动机运转噪声片段(1 400点)作Monte Carlo仿真预测试验，结果见表3。由于模板噪声与实测噪声间相关性强弱的随机性要求滤波器具有良好的动态响应速度，因此，采用去相关NLMS自适应策略的Volterra滤波器的预测精度远高于其它滤波器。两路噪声相位不匹配(每个周期中d(m)相对模板噪声x(m)延后600点)会显著影响预测精度。

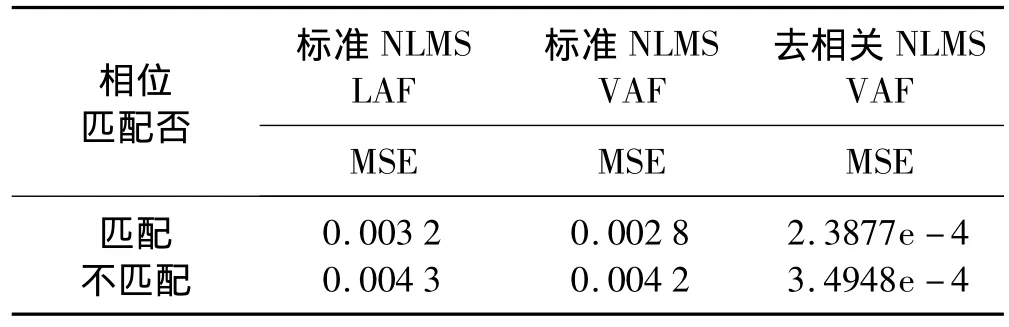
表3 相位匹配对预测误差的影响Tab.3 The influences of phase matching to prediction error

图6给出了去相关NLMS Volterra滤波器在相位匹配后进行的1次预测试验部分情况。可见，滤波器输出幅度及相位基本上能够以较高精度跟踪主通道现场实测的发动机运转噪声。

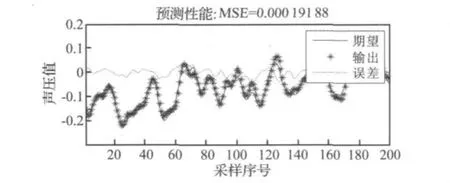
图6 基于模板噪声的发动机运转噪声预测Fig.6 Engine running noise prediction base on template noise

表4 转速波动对预测误差的影响Tab.4 The influences of rotating speed turbulence to prediction error

为了考察模板噪声对发动机工况波动时对应的实测噪声的适应性，分别采用1 000 r/min、1 500 r/min及2 000 r/min三种转速下发动机运转噪声作为模板噪声，对实测噪声采用去相关NLMS VAF进行4组Monte Carlo噪声预测仿真试验，每组试验采用相同发动机工况下的30个不同的运转噪声样本进行30次。结果见表4。

总体上看，用低转速模板噪声来预测相同转速或相对高转速的实测噪声信号，比用高转速模板噪声来预测相同转速或相对低转速噪声信号的精度要高。这是因为，转速相对低的噪声信号包含了更多的噪声细节信息，使得相同窗口宽度的低转速噪声信号表达高转速噪声信号的能力更强。此外还可看出，预测均方误差为10－4数量级，具有工程实用价值;实测噪声对应的转速在模板噪声对应的转速以上较小范围内波动时，预测精度下降不大，说明该方法的预测精度对于转速波动具有一定的鲁棒性。

4 结论

利用Volterra自适应滤波器可有效预测发动机运转噪声，其预测精度优于传统的线性自适应滤波器;去相关NLMS自适应Volterra滤波器可明显加快学习进度，缩短动态响应过程，有利于跟踪宽带噪声信号;基于模板噪声的预测方法，有效地利用了发动机运转噪声内在的循环相关信息，其精度可以满足实际应用，且对于转速波动具有较好的鲁棒性。基于噪声模板的预测方法使仅借助单传感器实现噪声对消成为可能，为提取或增强淹没于发动机运转噪声中的故障异响信号提供了新的思路和方法。

［1］张德麟.汽车声响与故障判断排除［M］.北京:金盾出版社，2005.

［2］刘艳梅，程 凯，鞠浩民，等.发动机异响信号的小波包能量特征提取［J］.机械制造与研究，2009，38(2):70－83.

［3］程利军，张英堂，罗 亮，等.柴油机缸盖噪声信号处理方法及故障诊断研究［J］.振动与冲击，2009，28(4):173－176.

［4］Lin J.Feature extraction of machine sound using wavelet and its application in fault diagnosis［J］.NDT ＆ E International，2001，34(1):25－30.

［5］Kimmich F，Schwarte A，Isermann R.Fault detection for modern Diesel engines using signal-and process model-based methods［J］.Control Engineering Practice.2005，13(2):189－204.

［6］Li Y J，Tse P W，Yang X，et al.EMD-based fault diagnosis for abnormal clearance between contacting components in a dieselengine［J］. Mechanical Systems and Signal Processing.2010，361(1):193－210.

［7］李 力，何 婷.小波能量商在汽车发动机故障诊断中的应用［J］.汽车工程，2009，31(2):193－196.

［8］徐礼超.基于模糊理论的发动机异响诊断方法研究［J］.煤矿机械，2007，28(11):195－198.

［9］魏少华.基于声强知识与神经网络融合技术的发动机故障诊断研究［D］.南京:南京理工大学，2006.

［10］侯温良.模拟听觉的机器故障诊断设备的框架［J］.声学技术，2003，22(4):223 －226.

［11］李 力，廖湘辉.发动机活塞异响声的循环统计量诊断法［J］.噪声与振动控制，2006，26(6):40 －42，45.

［12］ Haykin S.Adaptive filter theory［M］.郑宝玉等译.(第四版).北京:电子工业出版社，2003.

［13］ Vijaykumar V R，Vanathi P T，Kanagasapabathy P.Modified adaptive filtering algorithm for noise cancellation in speech signals［J］.Electronics and Electrical Engineering，2007，2(74):17－20.

［14］曹建福，韩崇昭，方洋旺.非线性系统理论及应用［M］.西安:西安交通大学出版社，2006.

［15］裘 焱，吴亚锋，李 野.应用EMD分解下的Volterra模型提取机械故障特征［J］.振动与冲击，2010，29(6):59－61，128.

［16］ Packard N H，Crutchfield J P，Frasher J D，et al.Geometry from a time series［J］.Physical Review Letters，1980，45:712－716.

［17］ Takens F.Detecting strange attractors in turbulence［J］.Lecture Notes in Mathematics，1981，898:366 －381.

［18］ Glentis G O，Berberidis K，Theodoridis S.Efficient least squares adaptive algorithms for FIR transversal filtering［J］.IEEE Signal Processing Magzine，1999，16(4):13－41.