高频磁场环境下热电偶测温研究

林苏斌，陈 为，汪晶慧

(福州大学电气工程与自动化学院，福建 福州 350108）

高频磁场环境下热电偶测温研究

林苏斌，陈 为，汪晶慧

(福州大学电气工程与自动化学院，福建 福州 350108）

在高频磁场环境下采用热电偶测温时，会存在很大的误差。本文分析了误差产生的机理，指出测温误差是由于高频磁场环境下热电偶金属端部的涡流效应产生较大的损耗密度所引起。在电磁场理论分析的基础上，搭建了热电偶高频磁场环境测温平台，结合测量结果，采用多元非线性回归算法建立了正弦波磁场环境下的K型热电偶温升模型，以修正高频磁场涡流效应的影响。利用加权平均等效正弦频率的方法，将正弦波磁场激励下的热电偶温升模型应用于方波电压激励下的三角波磁场测温环境。实验验证了本文建立的模型在正弦波与三角波高频磁场下具有很高的测温精度。

热电偶;高频磁场;温升模型;涡流

1 引言

高功率密度是开关电源发展的方向之一，随着开关电源工作频率不断提高，输出电流不断增大，高频功率磁性元件以及开关器件的损耗也在急剧增大，严重影响产品的可靠性和安全性［1］，因此有必要对开关电源温升进行准确测量。由于磁性元件体积大，不易散热，成为开关电源的最热点。GB 4943—2001对开关电源产品温升测量指出:如果未规定具体的测量方法，应采用热电偶法或电阻法来测量绕组的温度，对除绕组以外的零部件的温度，应采用热电偶法来测定［2］。功率器件温升的测量比较容易实现，对于磁性元件的温升测量，电阻法只能得到绕组平均温升，得不到温升最高点。目前工程上只能采用热电偶测量线圈表面温升，再通过经验估算内部温升的方法，但这种方法明显存在较大误差。目前国内外相关文献对热电偶测温误差进行分析，主要集中在热电偶本身的劣化误差，热电偶冷端温度不为零引起的误差，被测温度与热电偶输出热电势非线性引起的误差［3-4］等。

为了准确评估磁性元件绕组内部的温升情况，需要直接将热电偶埋在绕组内部测量温升，如图1所示。在实际温升测试中，发现埋在原、副边绕组之间的热电偶1的温升要明显大大高于埋在线圈表面热电偶2的温升，两者温差可高达100多度，这一现象，显然无法用绕组损耗引起的温升来解释。从图1的磁场分布可以看出:虽然绕组外部热电偶2所处位置的磁场为零，但绕组内部热电偶1位置却存在一定的漏磁场，因此绕组内部的热电偶是处在高频磁场环境下，虽然这个磁场很小，一般只有毫特级，但在千赫兹高频作用下，就可能带来额外损耗和温升。

图1 高频变压器结构及磁场分布Fig.1 High-frequency transformer and magnetic field

本文主要针对高频磁场环境下热电偶测温应用进行研究，以K型热电偶为例，分析 K型热电偶在高频磁场环境下测温时产生误差的机理，建立K型热电偶在高频磁场环境下温升数学模型，可有效修正K型热电偶在高频磁场环境下测温误差。

2 热电偶在高频磁场环境下涡流损耗分析

金属导体在高频磁场环境中会产生涡流，造成涡流损耗［5-6］。K型热电偶材料为镍铬-镍硅合金，具有一定的电导率，在高频磁场环境下测温时，热电偶端部将感应出涡流，产生涡流损耗。虽然这一涡流损耗本身很小，但热电偶端部体积很小，因此损耗密度很大，从而使得端部急剧升温。基于这个假设，把热电偶端部近似看做一个小圆柱导体，如图2所示。

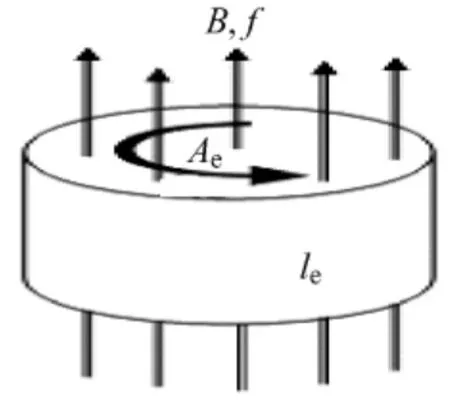
图2 热电偶涡流示意图Fig.2 Schematic diagram of thermocouple eddy current

根据电磁感应定律:

如果磁场随时间做正弦规律变化，由式(1）可得:

高频磁场中导体涡流损耗为

式中，Ae为K型热电偶偶丝截面积;le为K型热电偶偶丝长度;σ为K型热电偶电导率。

由式(5）可知，理想情况下，K型热电偶涡流损耗与热电偶偶丝本身的电导率，周围电磁场的频率及磁通大小有关。但实际上，热电偶偶丝端部并不是理想的圆柱体，其电导率也不是单一合金的电导率，但根据涡流的机理，涡流损耗与磁场频率f以及磁感应强度B的幂指数有关［7］，因此对式(5）做进一步修正:

式中，k1，α1，β1为待定系数。

根据温升公式:

式中，k2，α2，β2为待定系数。

再考虑环境及热电偶导线散热，热电偶在高频磁场环境测温时，涡流损耗引起的温升为:

式中，k2fα2Bβ2为涡流损耗引起的温升;k3fα3Bβ3为环境及热电偶导线散热引起的温升。

3 热电偶高频磁场环境测温实验平台

为了准确评估热电偶在高频磁场环境下的损耗带来的附加温升特性，本文建立了图3所示高频磁场测温实验平台。测温平台由信号发生器产生高频正弦波，经过功率放大器放大后施加给空心螺线管，从而在空心螺线管中产生均匀的磁场环境。K型热电偶(实验用热电偶型号为:KP-I-0.8-GB/T 2614—1998偶丝直径为0.8mm）置于空心螺线管内部测温。空心螺线管线圈采用0.1mm×100股利兹线绕制，以降低线圈温升对测温的影响。将空心螺线管放置在一个封闭的盒子内，避免了周围空气对流对测温的影响。在不同频率与磁感应强度下，测量热电偶温升。正弦波激励下，磁感应强度与K型热电偶温升的趋势图如图4所示。从图中可以看出，在频率相同的情况下，施加的磁感应强度越大，K型热电偶温升也越大。正弦波激励下，频率与K型热电偶温升的趋势图见图5。从图中可以看出，磁感应强度相同的情况下，施加的电磁场频率越高，温升也越大。根据式(5），在不考虑环境及热电偶导线散热以及涡流反磁场情况下，涡流损耗与频率的2次方，以及磁感应强度的2次方成正比。这与实测的磁感应强度与温升趋势图中的温升曲线上升趋势不符，同样，图5中频率与温升趋势图中温升曲线也与本文式(5）存在较大偏差，因此本文采用综合考虑各种影响因素后经过修正的式(8），并利用多元非线性回归算法确定K型热电偶高频电磁场环境测温温升数学模型。

4 K型热电偶高频磁场环境测温温升数学模型

图3 热电偶高频电磁环境测温原理图Fig.3 Schematic diagram of temperature measurement in HFEF

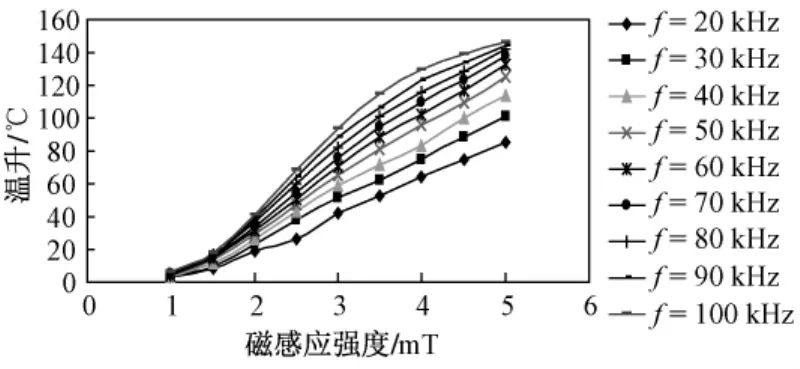
图4 磁感应强度-温升曲线Fig.4 Flux density-temperature rise curve

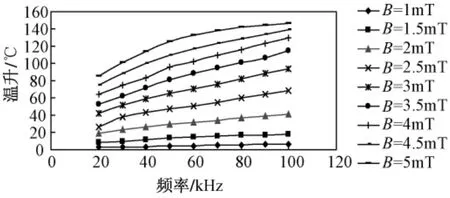
图5 频率-温升曲线Fig.5 Frequency-temperature rise curve

确定K型热电偶高频磁场环境测温温升数学模型的关键是确定式(8）中的待定系数，本文以不同磁感应强度及不同频率下的高频磁场实测温升数据为输入，按式(8）的形式构造回归方程，并给定待定系数初值，基于nlinfit非线性回归算法，确定待定系数，其流程如图6所示。

图6 热电偶温升数学模型流程图Fig.6 Flow chart of model of temperature rise

确定的K型热电偶正弦波高频磁场环境测温温升数学模型为:

5 磁通波形为三角波的高频磁场热电偶测温模型

开关电源中的磁件大多数工作在方波或者矩形波电压激励下，此时电磁场随时间呈三角波变化，因此有必要在上述正弦波激励下热电偶测温模型的基础上，进一步分析三角波规律变化的电磁场环境下热电偶温升模型。在磁芯损耗计算中可根据修正的斯坦麦茨公式(Modified Steinmetz-Equation，MSE）计算方波或矩形波激励下的磁芯损耗。并可计算出等效正弦频率。MSE在计算方波或矩形波激励下磁芯损耗时认为磁芯损耗主要与经过加权处理的磁化速率dB/dt相关［8-10］。热电偶在高频磁场环境下测温产生误差的原因是其偶丝端部在磁场环境中产生涡流损耗引起的额外温升，与磁芯损耗产生的机理类似，因此本文根据MSE的原理确定方波或矩形波电压激励下的热电偶端部涡流损耗。求出的等效正弦频率可表示为:

式中，fsin.eq为等效正弦波频率;T为方波周期;ΔB是磁密峰峰值。

方波激励的等效频率见表1。因此对于电压是方波或矩形波激励下的高频电磁场下热电偶测温模型也可用式(9）的正弦波温升模型表示，在应用时将式(9）中的频率用等效正弦波频率替换。

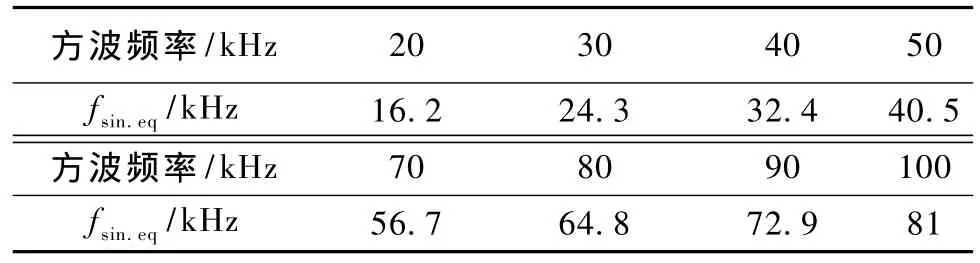
表1 方波激励的等效正弦波频率Tab.1 Sine wave equivalent frequency

6 K型热电偶高频电磁场环境测温温升数学模型精度验证

为了验证温升模型的精度，选取了几组不同频率及磁感应强度，分别对正弦波电压激励和方波电压激励下的高频磁场环境进行测试，验证K型热电偶高频磁场环境测温温升数学模型，表2为正弦波电压激励的验证数据，表3为利用加权平均等效正弦频率方法的方波电压激励验证数据，从表2可以看出正弦波激励时最大相对误差为12%，从表3可以看出方波激励时最大相对误差为9%，在两种情况下都完全满足精度要求。

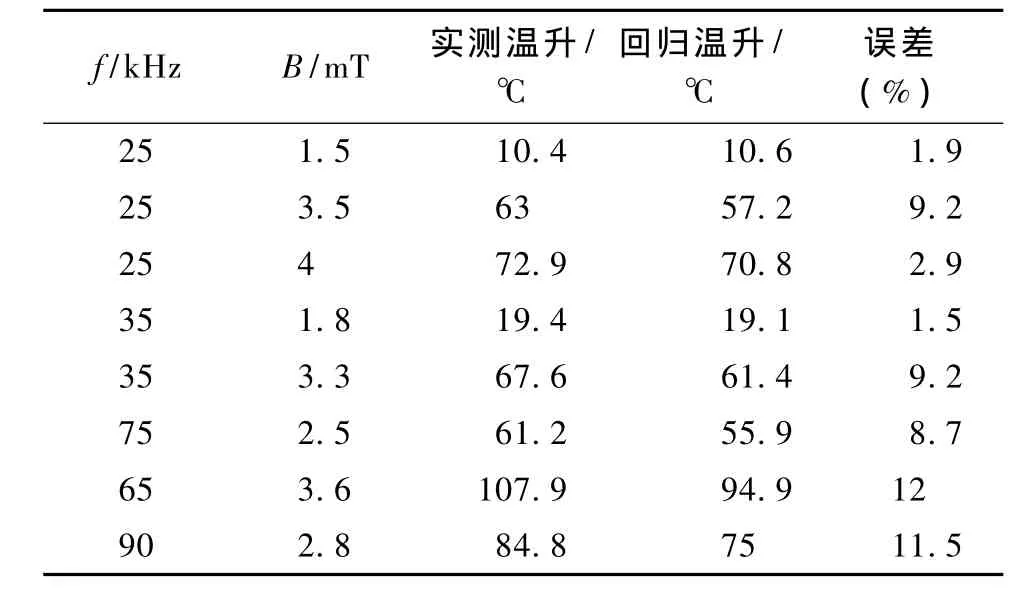
表2 正弦波电压激励验证数据Tab.2 Sine excitation verification data

表3 方波电压激励验证数据Tab.3 Square excitation verification data

7 结论

(1）研究发现，热电偶在高频磁场环境测温时，由于涡流效应会引起合金偶丝端部很大的损耗密度，从而带来额外温升，使读数不能客观表达测温点的温升，存在很大误差。即使在毫特级磁场下，也会带来较大的额外温升。

(2）通过建立高频磁场测量环境，基于nlinfit回归算法建立了正弦波磁场环境下K型热电偶(型号为:KP-I-0.8-GB/T 2614—1998偶丝直径为0.8mm）温升模型，模型考虑了涡流效应带来的额外温升对测量的影响。

(3）针对高频方波电压激励下的三角波磁场环境，利用等效加权平均磁通变化率的概念，引入等效正弦频率，将正弦波磁场热电偶温升模型扩展应用于方波磁场环境下。

(4）实验验证了温升模型在正弦波磁场环境下最大相对误差12%，在方波电压激励下三角波磁场环境下最大相对误差9%，完全满足工程应用精度要求。

(5）本文提出的方法和模型也适用于其他类型和尺寸的热电偶(热电偶丝的电导率、磁导率以及偶丝测温端部直径），只是模型的系数需要通过实验回归确定。

References）:

［1］毛行奎，陈为 (Mao Xingkui，Chen Wei）.开关电源高频功率平面变压器热设计研究(Thermal design considerations for high frequency power planar transformer）［J］.电工电能新技术 (Advanced Technology of Electrical Engineering and Energy），2007，26(4）:21-25.

［2］GB 4943—2001，信息技术设备的安全［S］.

［3］刘丁，李晓斌，左磊 (Liu Ding，Li Xiaobin，Zuo Lei）.基于最小二乘支持向量机的N热电偶非线性校正及应用(Nonlinear calibration for N thermocouple sensor based on least squares support vector machine）［J］.仪器仪表学报(Chinese Journal of Scientific Instrument），2007，28(4）:640-643.

［4］郝晓剑，李科杰，周汉昌，等 (Hao Xiaojian，Li Kejie，Zhou Hanchang，et al.）.热电偶动态测量误差补偿技术研究 (Research on dynamic measurement errors compensation technology of thermocouple）［J］.中北大学学报(自然科学版）(Journal of North University of China(Natural Science Edition）），2008，29(4）:370-375.

［5］Islam M J，Khang H V，Repo A K.Eddy-current loss and temperature rise in the form-wound stator winding of an inverter-fed cage induction motor［J］.IEEE Transactions on Magnetics，2010，46(8）:3414-3416.

［6］Wang Shishan，Ji Shengchang，Li Yanming.The study of eddy current losses in coaxially insulated windings of power transformer［A］.Proceedings PowerCon 2002 International Conference on Power System Technology［C］.2002.3:1392-1395.

［7］李立毅，严柏平，张成明 (Li Liyi，Yan Baiping，Zhang Chengming）.驱动频率对超磁致伸缩致动器的损耗和温升特性的影响 (Influence of frequency on characteristic of loss and temperature in giant magnetostrictive actuator）［J］.中国电机工程学报(Proceedings of the CSEE，2011，31(18）:124-129.

［8］Marcelo S Lancarotte，Clovis Goldemberg，Aderbal de Arruda Penteado.Estimation of FeSi core losses under PWM or DC bias ripple voltage excitations［J］.IEEE Transactions on Energy Conversion，2005，20(2）:367-372.

［9］Li Jieli，Tarek Abdallah，Charles R Sullivan.Improved calculation of core loss with nonsinusoidal waveforms［A］.Industry Applications Conference，2001.Thirty-Sixth IAS Annual Meeting.Conference Record of the 2001 IEEE［C］.2001.2203-2210.

［10］ Jonas Muhlethaler，Jurgen Biela，Johann Walter Kolar，et al.Core losses under the DC bias condition based on steinmetz parameters［J］.IEEE Transactions on Power Electronics，2012，27(2）:953-963.

Study of temperature measurements with thermocouple under high-frequency magnetic field

LIN Su-bin，CHEN Wei，WANG Jing-hui
(College of Engineering＆ Automation，Fuzhou University，Fuzhou 350108，China）

The measurement error of temperature by thermocouple is very large when it's used to measure the temperature in environment with high-frequency magnetic field.In this paper the mechanism of errors is analyzed to find that the error was due to eddy-current effect on the metal tip of the thermocouple.The thermocouple temperature measuring platform in high-frequency magnetic field was built.With the results of measurement，temperature rising model of K type thermocouple under the sine wave magnetic field was set by use of multiple nonlinear regression algorithm in order to amending the influence of eddy current effect.Based on the method of weighted average equivalent sine frequency，sine wave of magnetic field temperature rising model is applied to triangular wave magnetic field.Experiments verified the temperature rising model is accurate enough for the sine wave，and even for the triangular wave high-frequency magnetic field.

thermocouple;high-frequency magnetic field;temperature rising model;eddy current

TM277.1

A

1003-3076(2012）04-0062-04

2012-02-06

国家自然科学基金(50877010）和福建省教育厅资助项目(JA11028）

林苏斌 (1977-），男，福建籍，讲师，博士生，研究方向为电力电子高频磁技术;

陈 为 (1958-），男，福建籍，教授/博导，研究方向为电力电子高频磁技术及电磁兼容。