一种平面射频发射线圈的电磁特性分析

魏树峰，杨文晖，王慧贤

(1.中国科学院电工研究所，北京 100190;2.中国科学院研究生院，北京 100049）

一种平面射频发射线圈的电磁特性分析

魏树峰1，2，杨文晖1，王慧贤1

(1.中国科学院电工研究所，北京 100190;2.中国科学院研究生院，北京 100049）

对一种应用在垂直场磁共振成像系统上的平面射频发射线圈进行了分析研究。首先用集中参数的等效电路模型对线圈的谐振频率及谐振模式进行了理论分析，在此基础上利用电磁场数值计算的方法对这种线圈在不同的谐振模式下的电流分布及磁场分布进行了研究。最后还对一个分成8段的平面射频发射线圈的射频场的空间分布进行了仿真。结果表明，这种线圈在300 mm的球内，磁场强度偏离中心点最大不超过15.2%，计算结果与实测结果是吻合的。

磁共振成像(MRI）;射频线圈;垂直场;电磁场数值计算

1 引言

现在MRI已有广泛应用与临床，对医学诊断具有重要的意义。开放式磁共振成像系统由于其开放的结构，所以能为被检查者提供比较舒适的环境，非常适合于有幽闭症的患者进行检查，另外，开放式磁共振系统为介入治疗提供便利。

目前国内外对垂直场下的射频发射线圈研究相对较少。最初用于垂直场磁共振成像系统的射频线圈是马鞍形线圈［1］，这种线圈具有较好的均匀性和较高的发射效率，但是这种线圈相对封闭，不适合用于开放式磁共振成像系统，因此被后来出现的平板射频发射线圈所取代［2-3］。目前在商业化的磁共振成像系统中还出现了一种圆盘形的平面射频发射线圈［4］。但目前还没有相关的文献对这种线圈进行分析研究。和常规的线圈相比，这种线圈结构比较特殊，如图1所示，利用解析的方法对这种线圈进行求解分析是比较困难的。另外一种分析方法是用电磁场数值计算的方法来进行分析。本文尝试了用Ansoft Maxwell的涡流场求解器进行对上述线圈的磁场分布特性进行了分析。在下文中，首先介绍了这种线圈的结构，然后用等效电路的方法对线圈的谐振特性进行了分析，在此基础上应用电磁场数值计算的方法对不同谐振模式下，线圈内的电流分布以及相应模式下所产生的射频磁场的分布特性进行分析。最后对一个用于0.23T开放式磁共振系统的平面射频发射线圈的射频场进行了分析，并与实测数据进行了比较。

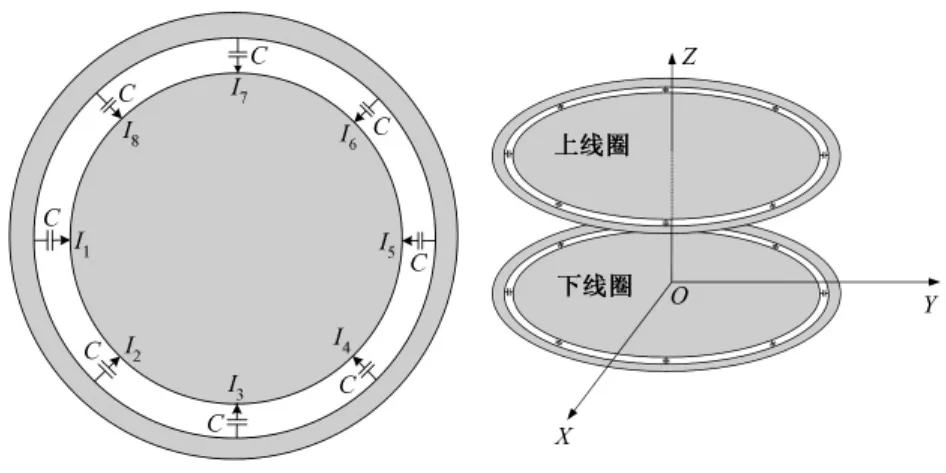
图1 线圈结构示意图Fig.1 Diagram of 8-leg planar birdcage coil

2 等效电路模型分析

本文介绍的平面射频线圈的结构如图1所示，线圈包括上下两个相同的平面线圈，每个线圈都由中心圆导体、外导体环构成。中心导体与外环回路之间均匀地分布着若干容值相同的电容。这种线圈在电气机构上与鸟笼线圈非常相似，因此也可以用一个集中参数的梯形低通网络等效电路模型进行分析［5］，如图2所示。N个电容将线圈均匀地分为 N段，构成N个电流回路，其中，L是第n段内导体的等效自感，L'是第n段外导体回路的等效自感，C是第n个电容器的容值，In是第 n个回路的电流。如果忽略了各导体段之间的互感，根据基尔霍夫电压定律，对上述电路求解可以得到的谐振频率为:

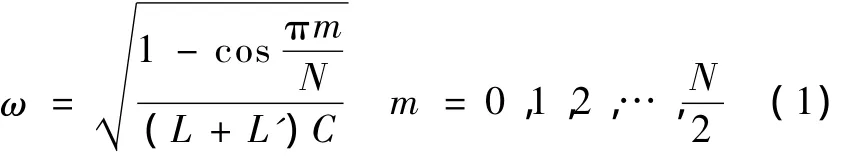
其中，ω为线圈的谐振频率;m为线圈的谐振模式;由式(1）可知，这种平面线圈具有和鸟笼线圈相似的多个谐振点，m取不同值对应线圈不同的谐振点，对一个分成N段的线圈，总共具有N/2+1个谐振模式。当m=0时，ω=0，即此时线圈中没有谐振现象，所以对于低通型线圈，通常不考虑这种情况。需要注意的是，由于式(1）忽略各段之间的互感，由式(1）得到的谐振频率会比实际的谐振频率偏低［6］。

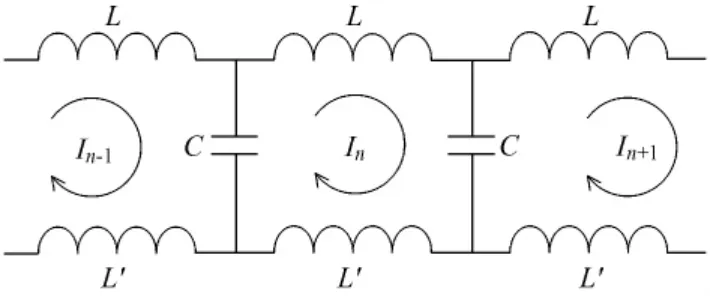
图2 平面线圈的集中参数等效电路图Fig.2 Lumped element equivalent circuit of planar coil

根据对鸟笼线圈的分析结果可知，对于上述低通结构的平面线圈，各跨接在线圈内外导体之间的电容上流过的电流按照余弦分布［7］，即:

其中，n为各段的序号;K为一个与n无关的常数。对于鸟笼线圈，不同的谐振模式下，线圈的各条腿上的电流分布不同，在线圈内产生的磁场差异也很大。对于上述平面线圈，不同的模式下，中心导体中的电流分布不同，因此在线圈平面附近区域内产生的磁场也各不相同。

3 不同谐振模式下的磁场分布特性

虽然上述平面线圈具有和鸟笼线圈相似的谐振特性，但是产生均匀的射频场的机理却完全不同。通电电流密度按照正弦分布的无限长圆柱面能在圆柱内产生一个均匀的磁场。鸟笼线圈正是依据这个原理，使各条腿中的电流按正弦分布，从而在线圈内产生一个非常均匀的磁场。但是对于上述平面线圈，原理上类似于无限大均匀载流平面在其上下两侧产生均匀的磁场，但是由于线圈工作在高频，而且线圈平面面积有限，因此只能在成像区域内产生一定均匀度的射频磁场。磁场的空间分布主要由流过内外导体上的电流决定，特别是内导电平面中电流的分布对所产生的磁场的分布是非常重要的。在射频条件下，电流在导体中集肤效应非常显著，另外由跨接在内外导体中的电容注入中心平板的电流对中心圆导体中的电流分布也有很大的影响，因此，要用解析的方法得到中心平板的电流分布，从而计算出线圈产生的磁场是比较困难的。

本文以一个分为8段的一个平面线圈为例，分析了m=1，2，…，4四种模式下，中心导体平面内的电流分布及其附近的磁场分布。线圈的中心导体的直径为700mm，内外导体之间的间隙为10mm，外导电环的宽度为15mm，将线圈均匀地分为8段，如图3所示。在内外导体的连接处设置电流激励，其中电流的分布按照式(2）进行计算，n的位置如图3所示。求解器选择涡流场求解器。求解频率为9.82MHz。计算结果如图4所示，其中左侧为平面线圈上的电流密度分布图，右边为距离线圈190mm的平面内的磁场强度矢量的分布图。从图4可以看出，只有在模式1(m=1）时，平面线圈的中心导体中电流方向是基本一致的，从导体的一端流到另一端，只有一个宏观的电流方向，在距离线圈190mm的平面内可以在靠近中心的区域内产生一个与电流方向垂直的比较均匀的磁场。而在其他模式下，由于中心导体内的电流有多个宏观的电流流向，由这种电流分布产生的磁场在空间中的分布很不均匀，特别是在靠近线圈中心轴线附近的区域，磁场强度的方向各异，幅值也很低，均匀性很差，如图4所示。对于射频发射线圈来说，最重要的就是要获得均匀的射频磁场，这样才能使成像区域内的样品的核磁矩获得相同的翻转角度。因此，只有模式1能用于磁共振成像中的射频激发。

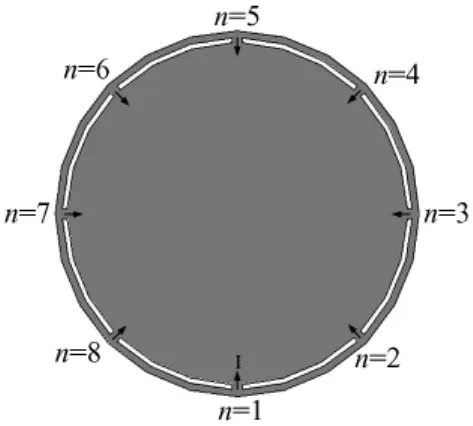
图3 线圈有限元模型结构图Fig.3 Finite element model of coil

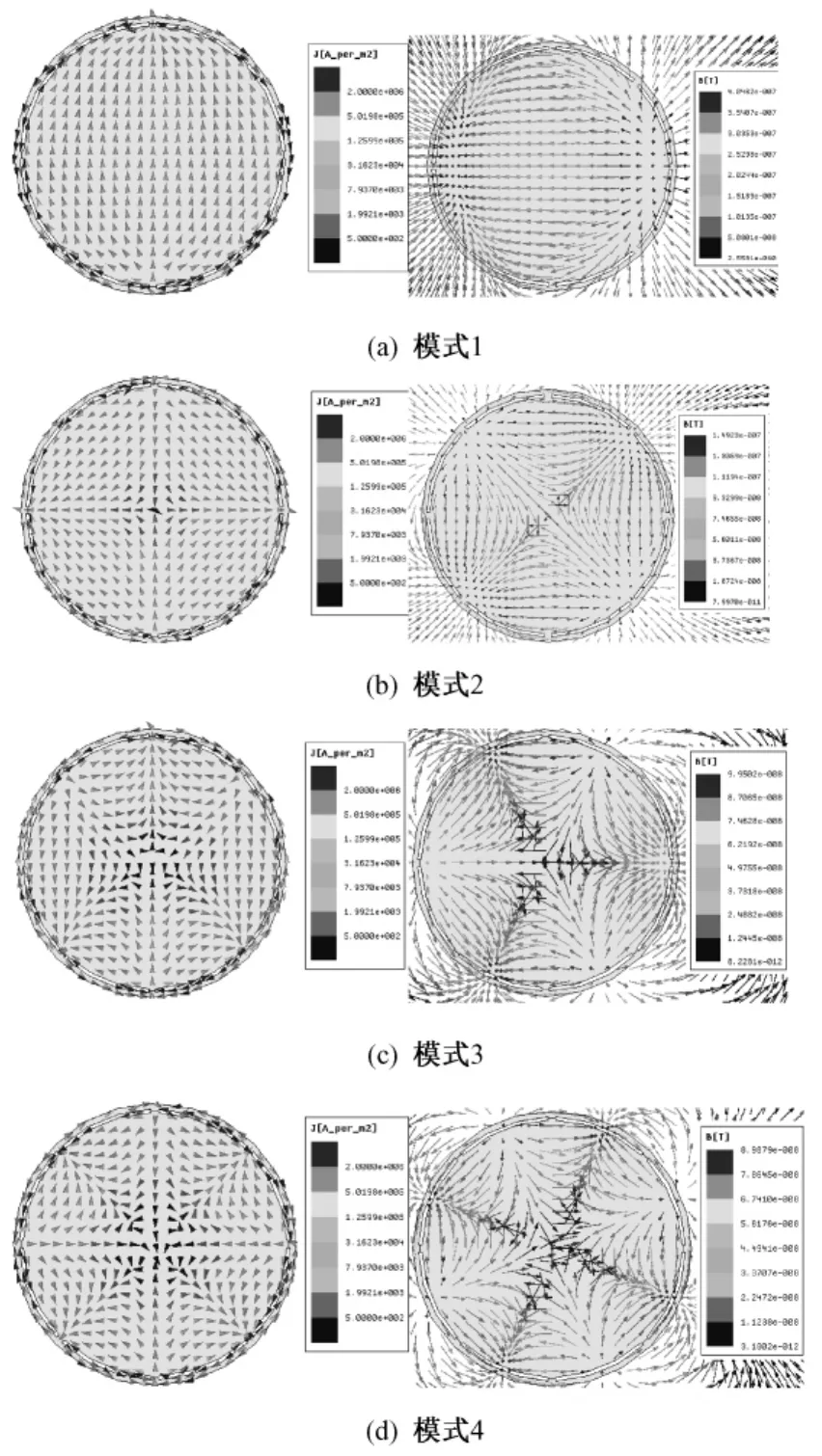
图4 不同模式下，平面线圈的电流密度分布(左图）以及磁感应强度的分布图(右图）Fig.4 Maps of current density on surface of planar coil(left）and magnetic field(right）

4 平面射频发射线圈均匀性计算

根据上述对不同模式下，线圈产生的磁场的分析结论，本文按照实际尺寸设计的分为8段的射频线圈的磁场分布特性。线圈的3D模型如图5所示，发射线圈包括上下两个平面线圈，单个线圈的模型与前文中的模型相同，上下两线圈的间距为380mm，线圈到屏蔽板的距离为35mm。在每一段连接内外导体的连接处施加电流激励，电流的每一段中电流的大小按照式(2）计算，其中按照K=1，m=1进行计算。要在两板之间产生均匀的磁场，上下两中心导体中流过的电流必须大小相等，方向相反。本文中使上板中的电流沿X轴负方向，下板中的电流沿X轴正方。求解频率选择为9.82 MHz(对应0.23T磁共振成像系统）。设定两线圈之间直径300mm的球内为成像区域，其磁场强度的分布图如图6所示。可以看出，沿 Z轴方向，磁场在中心点最低，越靠近线圈平面场越强。在XY平面内，磁场在中心点最强，远离中心点后，磁感应强度的值逐渐降低，沿Y方向，线圈磁场衰减得比较快，沿X轴的衰减比较慢，在300 mm的球内，最大值点位于Z轴上距离中心150mm的点，而最小值点位于Y轴上距离中心150 mm处。

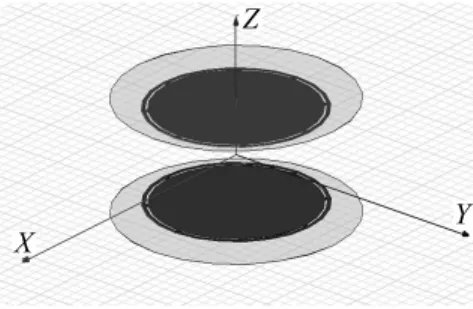
图5 射频发射线圈有限元Fig.5 Finite element model of RF transmit coil

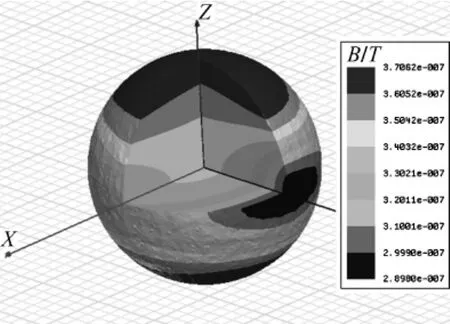
图6 磁场三维磁场强度分布图Fig.6 Map of magnetic field distribution

下面将上述计算结果与本实验室自制的与上述模型尺寸相同的平板射频线圈的测量数据进行了对比。图7所示即为测量线圈实物图。这里主要比较了沿轴线上的磁场强度矢量B(r）沿Y轴的分量By(r）的分布曲线，r为空间位置坐标。为了便于比较，计算值和实测值都用原点的值 By(0，0，0）进行标定。从图8中可以看出，计算值与测量值吻合得很好，由此也验证了上述仿真方法的准确性。

图7 线圈实物图Fig.7 A picture of the coil

图8 磁场均匀性沿X、Y、Z坐标轴仿真值与实测值的比较Fig.8 Comparison of homogeneity of magnetic field between simulation and measurement

5 结论

本文对目前的一种用于开放式磁共振成像系统的平面射频发射线圈进行了分析，在理论分析的基础上，对其在不同模式下的电流分布特性及其磁场分布特性进行了分析，分析的主要工具是 ansoft maxwell3D有限元计算软件。另外还按照实际的尺寸分析了一个分成8段的平面射频线圈的磁场的均匀性，并对计算数据和实测数据进行了比较，结果表明计算值与实测值非常吻合，由此也验证了此分析方法的可行性与准确性。希望本文的分析结果能为其他相关设计人员提供设计参考。

References）:

［1］Carlson J W，Gyori M，Kaufman L.A technique for MR imaging of the knee under large flexing angles［J］.Magnetic Resonance Imaging，1990，8(4）:407-410.

［2］McCarten B，Carlson J，Fehn J，et al.Open design and flat cross sectional RF transmit coil for transverse magnet based MRI systems［A］.Nuclear Science Symposium and Medical Imaging Conference［C］.San Francisco，CA，1993.

［3］Ed B Boskamp.Flat RF body coil design for open MRI［A］.Proceedings of 22nd Annual EMBS International Conference［C］.Chicago，IL，2000，3:2387-2389.

［4］Schulz V，Planar R F.Resonantor for open MRI systems［P］.US Patent:7432709B2，2005.

［5］Cecil E Hayes，William A Edelstein，John F Schenck，et al.An efficient，highly homogeneous radio frequency coil for whole-body NMR imaging at 1.5T［J］.Journal of Magnetic Resonance，1985，63(3）:622-628.

［6］Jin Jianming.Electromagnetic analysis and design in magnetic resonance imaging［M］.Boca Raton，CRC，1999.

［7］James Tropp.The theory of the bird-cage resonator［J］.Journal of Magnetic Resonance，1989，82(1）:51-62.

Electromagnetic characteristic analysis of a planar transmit coil

WEI Shu-feng1，2，YANG Wen-hui1，WANG Hui-xian1
(1.Institute of Electrical Engineering，CAS，Beijing 100190，China;2.Graduate University，CAS，Beijing 100049，China）

A planar RF coil used in vertical field MRI was analyzed in this paper.Firstly，a lumped element equivalent circuit of the planar coil was used to analyze the resonant frequency and resonant mode of the coil.Then current distribution and magnetic field distribution in different resonant modes were studied with the method of numerical calculation of electromagnetic fields.Finally，a planar transmit coil with 8 segments was analyzed.The homogeneity of the coil in a sphere of 300 mm in diameter is 15.2%，and this is close to the results measured on a real coil.

MRI;RF coil;vertical field;numerical calculation of electromagnetic fields

TM153+.5

A

1003-3076(2012）04-0015-04

2011-12-20

国家自然科学基金青年基金资助项目(50807050）

魏树峰 (1982-），男，山西籍，博士研究生，研究方向为中低场磁共振并行成像技术;

杨文晖 (1966-），男，湖南籍，正高级工程师，研究方向为电磁成像技术。