求解PDPTW的混合分组编码智能算法

张 倩，丁根宏

(河海大学理学院，南京 211100)

随着互联网的普及和信息技术的高速发展，人类进入了以网络为主的信息时代。基于Internet开展的电子商务已经逐渐成为人们进行商务活动的新模式。而物流是电子商务的核心力量，其快速、通畅是电子商务可以正常、顺利进行的一个重要保证［1］。

车辆路径问题(vehicle routing problem，VRP)［2］是物流配送系统中的关键环节，是在1959年由Dantzig和Ramser共同提出的。车辆路径问题是近年来研究的一个热点问题，其中最广泛关注的问题如快递问题中的线路优化问题、信件运输与投递问题等［3］。

PDPTW［4－5］是一类具有广泛实际应用的优化组合问题。PDPTW是指一列车队必须完成的运输需求，装货点和卸货点是组成运输任务的2个需求要素。配送中心的每辆车从车库出发，沿所选的最优化路线为客户服务，以满足客户的运输需求，并最终返回车库。车辆在访问客户点时，必须依次服务所有需求，且满足时间窗、负载的限制，并最终返回车库。要用最大装货量和装载货物类型来限制每辆车，但是由于装货点和卸货点所在的实际位置不同，所以车辆必须在给出的时间窗口范围内访问到每个客户点。在解决PDPTW问题时，为了方便，定义其为整数线性规划问题。由于PDPTW问题比VRP问题多了时间窗限制，所以PDPTW是对VRP的扩展，VRP又是TSP的一种推广，而TSP已被证明是一个NP－hard问题［6］。因此，在解决PDPTW也具有许多类似的实际困难。由于PDPTW可以作为物流中运筹规划问题的模型，在实际生活中的应用越来越多，从而引起国内外学者的广泛关注。

1 PDPTW描述及模型

根据上述对PDPTW问题的定义，给出该问题的总体描述:首先设定不限定配货车辆的数目，并设负载Q都相同。设有1个中心车库，需要对L个客户点进行配送服务，令i为变量，i=1，2，…，L。定义客户点 i的装货地点为 i，卸货地点为L+i，用点O和2L+1表示中心车场。由于所处的地理位置可能不能和点一一对应，每个货物都有各自的装货点和卸货点，故有可能出现同一个点既是装货点又是卸货点的情况。设N={1，2，…，L，L+1，…，2L}为所有装货点与卸货点的集合。P+={1，2，…，L}为装货点集合，P－={L+1，L+2，…，2L}为卸货点集合，V={0，2L+1}为中心车场集合，N*=N∪V，M={1，2，…，m}为车辆集合。车辆在客户点i的货物装卸量为qi，i∈N。要从点i运到点L+i，qi为正数时则为装货，为负数时则为卸货，车辆k运输到客户点i时的负载量为 zik。设点 i的装货时间窗口为［ei，li］，卸货时间窗口为［eL+i，lL+i］，［e0，l0］表示车辆从中心车场开始的时间窗口，［e2L+1，l2L+1］表示回到中心车场的时间窗口。∀i，j∈N*，tij代表从点 i到点 j的行驶时间，cij代表从点i到点j的行驶距离，si为车辆在客户点i处的服务时间，ti为车辆在客户点i开始服务的时间，ei表示为允许客户点i服务的最早时间，li表示为允许客户点i服务的最迟时间，这里［ei，li］表示一个时间窗。从中心车场派出车辆，为这些客户点的需求进行服务，并且在客户点规定的时间窗内进行服务，最后要返回到到中心车场，要求找到使用车辆总费用最少的车辆路径方案。

针对上面的描述，将引进2个变量:

数学模型［7］为:

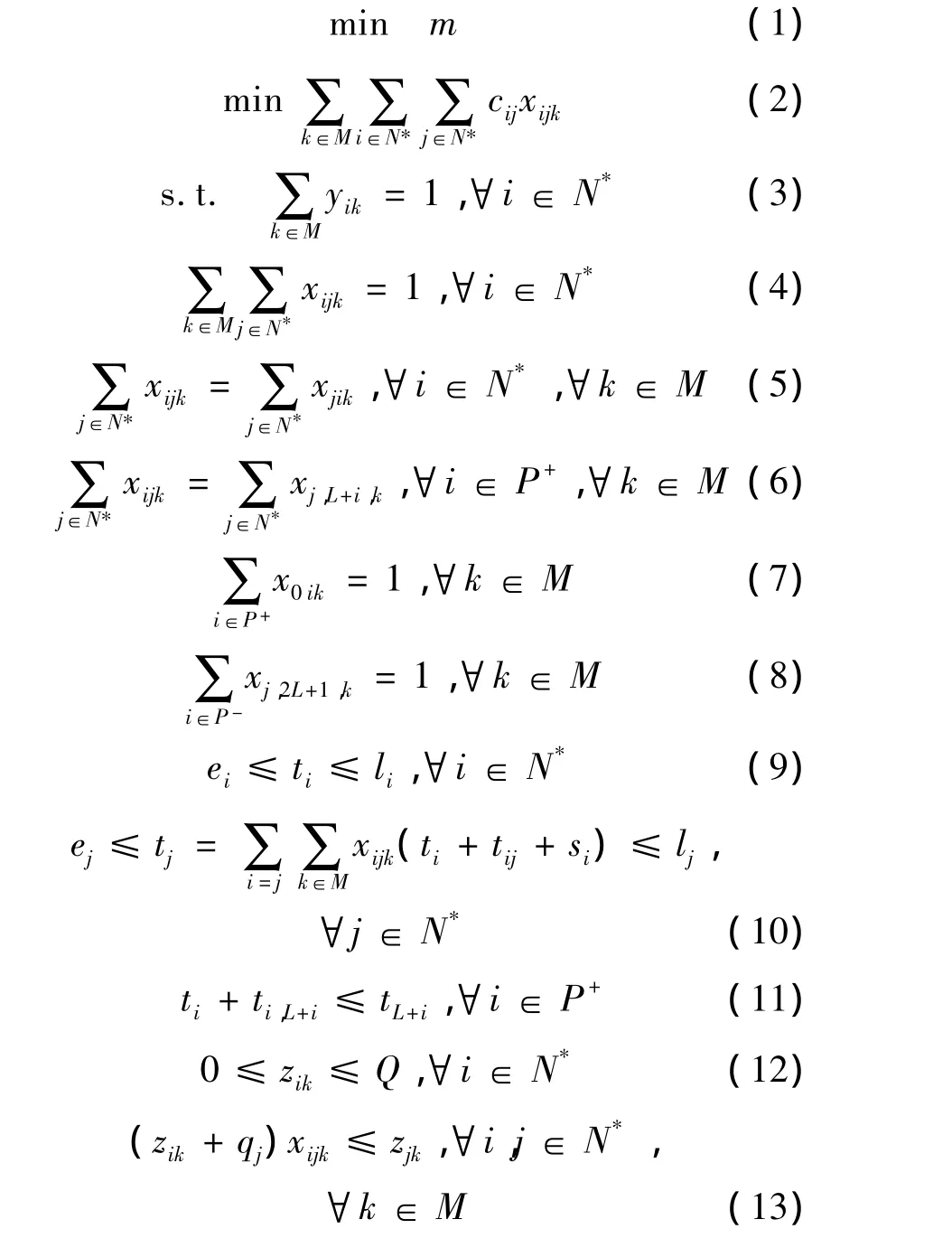
在此模型中:式(1)、(2)是目标函数，分别是车辆的数目与每个车辆行驶距离;式(3)表示每个客户点只被服务1次;式(4)、(5)表示每个客户点只有1辆智能车进行服务;式(6)表示一个客户的装货点与卸货点必须由同一辆车进行服务;式(7)、(8)表示车辆必须从中心车场出发，最后要返回至中心车场;式(9)～(11)表示时间窗、前序;式(12)、(13)是车辆负载。

由于PDPTW是多目标优化问题，本文主要研究的优化目标为:① 使用车辆总数最小;② 行车总距离最小，即车辆行驶路线的总长度最小。

2 混合分组编码智能算法

为减少PDPTW问题的计算复杂度，本文提出了一种混合分组编码智能算法来求解此类问题。该算法结合了遗传算法与粒子群算法在解决PDPTW时的优点。

粒子群算法是一种基于群体迭代的优化算法，该算法通过粒子个体之间的互相协助来寻找最优解。叶海燕等［9］提出了分组粒子群算法，这种算法其实是对粒子群算法的一种改进，该算法在运行时将种群分成若干个小组，对每个小组分别设置不同的算法参数进行搜索和优化。本文将继续采用粒子群算法来搜索不容易搜索到而且精度较高的解。

遗传算法是一种新型的全局优化搜索算法，它的基本思想就是模拟达尔文适者生存的自然选择和遗传机理的进化过程，对优化组合问题中的NP-hard问题的求解非常有效。商丽媛［7］在Giselher Pankratz提出的一种分组编码遗传算法［8］基础上，给出了一种多策略分组编码遗传算法，并用该算法对国际上的算例集进行计算，结果表明，该算法的搜索性能比国际上的其他算法要好。本文将在混合分组编码智能算法后期采用上述改进的分组编码遗传算法来进行优化求解。

混合分组编码智能算法的步骤:

第1步随机产生1个初始种群P，设定种群规模;

第2步先采用分组粒子群算法进行m次迭代，将初始种群P分成m个小组，在每个小组中对各自的参数进行初始化;

第3步在各个小组内独立进行粒子群优化迭代，迭代周期为t，对各小组进行相同次数的种群变异和重组操作;

第4步更新各小组中各自的参数;

第5步继续进行迭代，若满足终止条件继续第6步，否则返回第3步;

第6步对种群实施多策略分组编码遗传算法优化，根据个体适应度值排序保优;

第7步对选择后的种群进行交叉操作;

第8步交叉后的种群进行选择操作，排序保优;

第9步算法继续进行优化，当满足算法的终止条件时停止，否则返回第6步。

混合分组编码智能算法流程见图1。

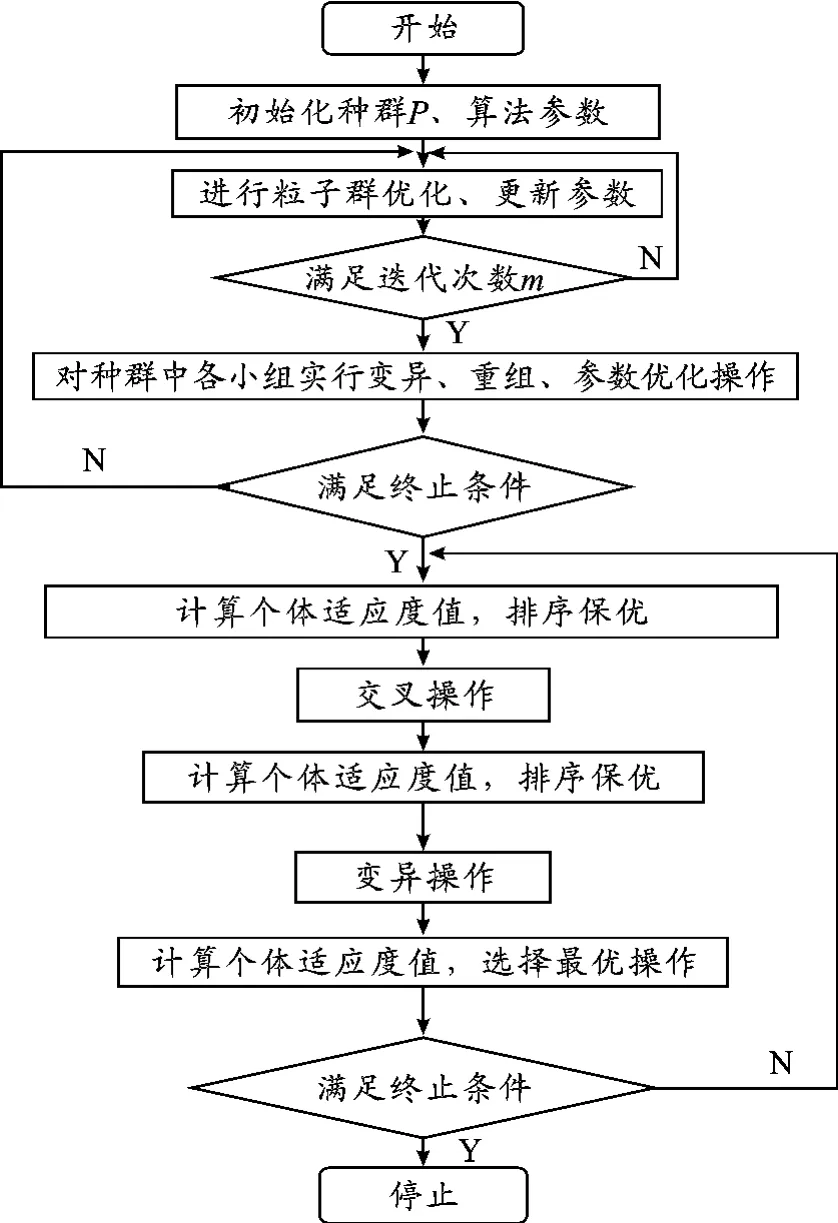
图1 混合分组编码智能算法流程

3 实例计算

下面给出PDPTW中简单的算例来分析混合分组编码智能算法性能。

以某县为例，县邮政局M辖有16个邮政支局。该县邮局M每天将从市局送来的邮件派送到所辖支局，并将由这些支局收寄的邮件运回县局X。邮车每天早上9:00出发，最迟15:00回到县局。邮车平均时速为30 km/h，邮车在支局卸装邮件耗时5 min，每辆邮车最多容纳65袋邮件。以县局M及其所辖的16个支局为研究对象，在规定的时限以及邮车容量的约束下，以邮车数量最少、邮车所行驶的总邮路里程最短为优化目标，合理规划邮路。表1为每个支局的邮件量。表2为县支局之间的距离。

表1 每个支局的邮件量

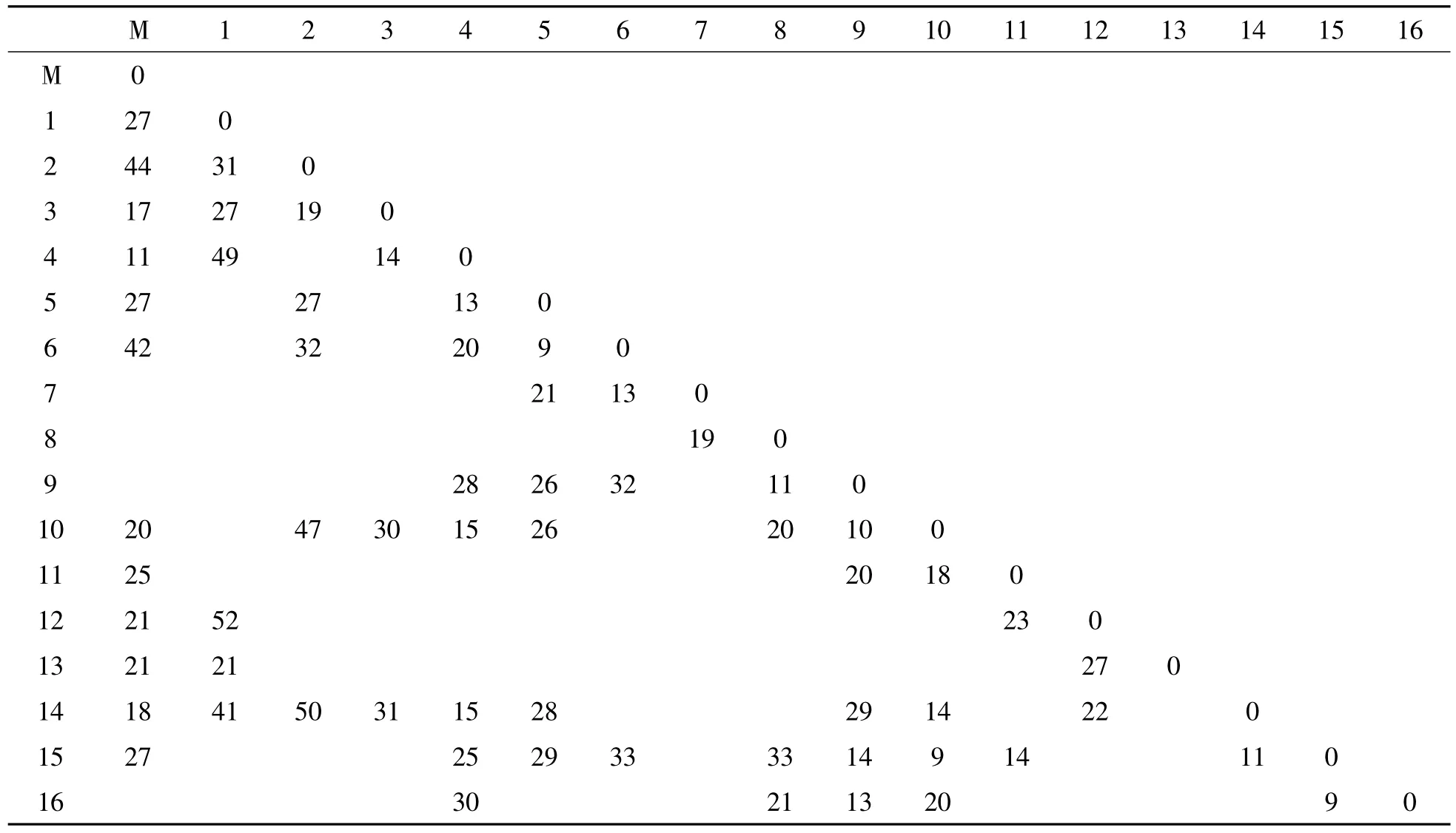
表2 县支局之间的距离 km

由表1中数据可知，寄达各支局的邮件量为176袋，而从支局收寄的邮件量为170袋。由于邮车最多容纳65袋邮件，所以可计算出县局至少需要3辆邮车才能满足该县的邮件运输需求。得到最少邮车数量为3。

有些文献中还考虑以空车率造成损失最小为优化目标，但经过测试发现，在最小化空车率造成损失时，虽然目标值有一定减小，但却造成运行里程和时间的大幅增加，综合考虑成本时仍是增加的。追求降低空车率会与追求最短里程相冲突，所以这里不予考虑空车率目标。

以总邮路里程最短为目标，即

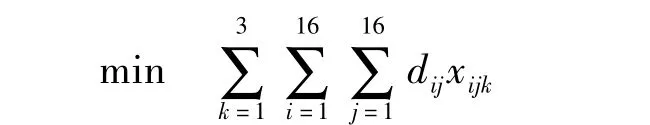
约束条件包括时间约束:

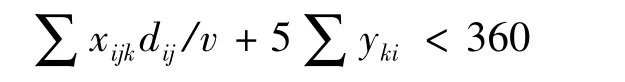
容量约束:

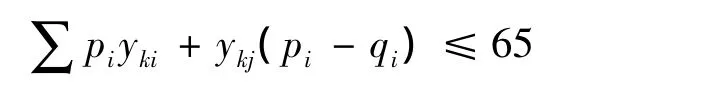
采用混合分组编码智能算法进行迭代。得到最优路线为:

车1路线:M—13—1—2—3—4—M

车2路线:M—10—9—8—7—5—6—(4)—M

车3路线:M—14—15—16—(15)—11—12—M

注:括号内表示邮车只经过而不装卸邮件。

将算法计算的结果与相同实例的其他算法计算结果进行比较，得到如表3结果。

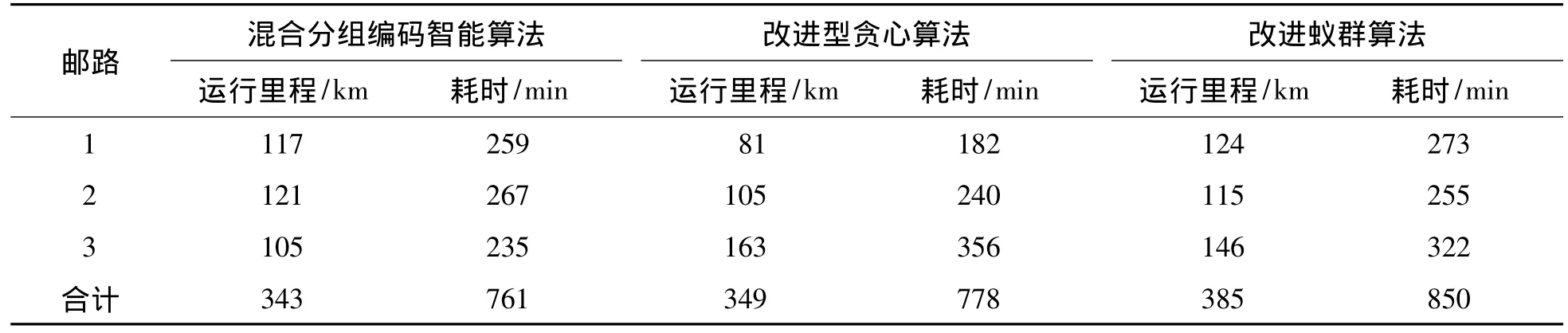
表3 各算法结果的比较

上述所有测试都是在PC(Inter，2.40 GHz)机上进行的。由表3可以看出，混合分组编码智能算法求解的总花费时间最少，相对于改进型贪心算法［9］和改进蚁群算法［10］，路程缩短了，时间节省了，解的精度更高。

4 结束语

本文在描述PDPTW问题的基础上，将粒子群算法与分组编码遗传算法相结合，提出了一种混合分组编码智能算法。但该算法在计算PDPTW算例时，只是在相对简单的算例上得到较好的解，而对国际上的某些算例集还不能达到理想的效果，所以还需对算法进行进一步的改进。

［1］刘华军，刘军.电子商务对物流及其管理的影响［J］.商品储运与保护，2001(1):25－29.

［2］Dantzing G，Rasmer J.The truck dispatching problem［J］.Management science，1959，(6):80 －91.

［3］李军，郭耀煌.物流配送车辆优化调度理论与方法［M］.北京:中国物资出版社，2001.

［4］Savelsbergh M W P，Sol M.The General Pickup and Delivery Problem［J］.Transportation Science，1991(29):17－29.

［5］Dumas Y，Desrosiers J，Soumis F.The Pickup and Delivery Problem with Time Windows［J］.European Journal of Operational Research，1991(54):7 －22.

［6］Lenstra J K，Rinnooy K.Complexity of Vehicle Routing and Scheduling Problem［J］.Networks，1981，40(2):221－227.

［7］商丽媛，丁根宏.有时间窗装卸问题的多策略分组编码遗传算法［J］.数学的实践与认识，2010，40(2):8－14.

［8］Giselher Pankratz.A Gouping Genetic Algorithm for the Pickup and Delivery Problem with Time Windows［J］.Operatons Research，2005(27):21 －41.

［9］叶海燕，陈毓灵，高鹰.分组粒子群优化算法［J］.广州大学学报，2007，6(2):64 －67.

［10］胡震宇，吴华玉，唐燕.邮政运输网络中的邮路规划和邮车调度［J］.数学实践与认识，2008，38(14):210－221.

［11］商丽媛.车辆路径问题遗传算法的设计与分析［D］.南京:河海大学，2006.