基于时域误差要求的巴特沃斯滤波器设计

翁剑枫

（浙江科技学院 信息与电子工程学院，杭州310023）

模拟滤波器在信号处理中起着重要的作用，从模拟信号采样前的限带滤波到数字处理后的信号重建恢复都须用到，因而在混合集成处理芯片中得到了广泛的使用。即就数字处理本身，实际使用的数字IIR滤波器也往往由其模拟原型进行变换得到，与FIR滤波器相比，虽然不具线性相位，但在相同的通带幅度特性情况下，IIR滤波器的复杂度即滤波器的阶次却远较FIR滤波器为低。因此，模拟滤波器至今仍是信号处理系统中的一个不可或缺的部分。

经典的模拟滤波器的设计技术已成熟多年［1－2］，设计过程非常简单，给定少量的频率参数和相应频率范围内的设计指标，套用公式即可完成低通原型设计，而且已有现成表格给出经频率变换后的各种实际使用的低通、带通、高通、带阻等滤波器的系统函数和结构。借助MATLAB，还可方便地从低通模拟原型滤波器构建出相应的任何阶次的IIR数字滤波器。但在实际应用中，除了通常的频域滤波外，还会遇到有时域性能要求的应用情况，如数据流传输中将会对所传输信号的波形失真也即时域误差提出要求，又如有些应用中系统对某种给定输入需要具有特定的响应形式，以及对滤波器的瞬态响应或阶跃响应有时间要求等。对于这种应用要求，由于无法将时域性能要求用作滤波器设计指标，因此也就无法直接采用上述广泛用于工程中的经典滤波器设计技术。文献［3－7］中给出了这类应用的一些例子，从中可见，为满足时域性能要求，滤波器的设计通常需要采用算法难度和实现复杂度均较经典滤波器情况为高的方法，如文献［3］所提出的时域综合方法完全基于非线性数值优化技术，文献［4］涉及了逆滤波误差准则及随后生成的一个线性系统的最优求解，而文献［5－7］则在经典滤波器基础上再采用了时变参数技术。文献［8］提出的方法虽简单，从理想传输条件下的系统函数出发，就贝塞尔滤波器的情况逼近得到了可实现的系统函数，但文中却并未涉及时域误差的定量分析，也未涉及其他设计指标。

从理论上说，将时域性能要求引入经典滤波器设计指标的主要障碍，是由于滤波器系统函数产生自其幅度平方函数。因此，不论使用何种形式的滤波器逼近方法，只有与幅度平方函数有关的性能要求才能在滤波器设计中用作设计指标，而滤波器的时域性能与其频率特性之间不存在解析关系，从而无法将这类要求取为经典滤波器的定量设计指标。

然而，进一步的考察表明，在众多的时域性能要求中，信号的时域误差在一定条件下是个例外。众所周知，信号经过滤波器后产生失真的来源有两个，一是滤波器的幅度特性非理想，另一是其不具线性相位特性。一方面，相位特性是由滤波器系统函数中分子分母的所有零极点的位置所形成，因此无法给出其对于线性相位特性的偏差表达，从而无法得到非理想相位特性对信号失真贡献的定量估计。另一方面，滤波器幅度特性与理想特性之间的差距则可以与所使用滤波器的幅度特性相联系。因此，去除相位特性非理想这一因素后，信号通过滤波器后产生的失真就完全由滤波器的幅度特性非理想所贡献。这样，只要导出由输出失真导致的误差信号的上界与所用滤波器的幅度平方函数之间的解析关系，就可将时域信号误差要求引入为滤波器设计指标，从而可以使用成熟的经典滤波器设计技术。不过，或许是由于经典滤波器设计从理论到技术都极为完备的缘故，迄今未见有对这个问题的探索。

由上述分析可知，在消除了滤波器非理想相位特性因素后，时域误差要求就有可能引入经典的模拟滤波器设计指标之中。为消除非理想相位特性这一因素，最简单有效的方法是对滤波器进行相位补偿，也即用全通网络对滤波器系统函数的零极点位置进行校正，使其具有近似的线性相位特性。各类经典滤波器形式中，贝塞尔或高斯滤波器具有十分出色的相位特性，但其幅度特性却远逊于巴特沃斯滤波器［1－2］。另外，巴特沃斯滤波器既具有最平幅度响应，又很容易用一个相对低阶的全通滤波器对其进行相位补偿。文献［2］中给出的一个实例表明，用4阶全通网络即可对一个10阶巴特沃斯滤波器实现接近理想的相位补偿，使其在群延迟特性及单位冲激响应和单位阶跃响应等方面均非常接近于理想滤波器。这样，为将时域误差要求引入到滤波器设计指标之中，采用相位补偿的巴特沃斯滤波器就是一个合理有效的选择。

本研究将根据上述思路，设法在经典滤波器设计技术中引入时域失真即时域信号误差指标。

1 滤波器输出的时域误差上界

对于有时域误差要求的应用情况，滤波器在滤除其通带以外杂散信号和噪声的同时，应使有用信号通过滤波器时尽可能不产生失真。在这种应用情况下，有用信号的带宽应是有限的，即输入信号是带限信号。现设滤波器的输入信号和输出信号分别为f（t）和g（t），相应的傅里叶变换分别为F（jω）和G（jω），滤波器的频率特性为

式（1）中，A（ω）｜max＝1，则相应的理想滤波器频率特性为

式（2）中，ωp大于信号的最高频率。

由式（1）～（2）可知，在频率范围｜ω≤ωp｜内，实际滤波器与理想滤波器之间幅度误差与相位误差分别为

对于实际使用的各种滤波器形式，显然都有0≤ΔA（ω）≤1。

不失一般性，令理想滤波器中的td＝0，则在频率范围｜ω≤ωp｜内，实际滤波器的频率特性可写为

信号f（t）通过滤波器H（jω）后的时域误差为

利用柯西－许瓦兹不等式，再利用帕斯维尔等式，从式（5）可得

式（6）中，L2范数 f（t）2是输入信号f（t）的均方根能量。注意到上式对任何t都成立，式（6）可进一步写为

式（7）中，e（t）∞为误差信号e（t）的契比雪夫范数，即e（t）的最大值。

由式（2）和（4），并计入理想滤波器的td＝0，则在滤波器通带范围内有

对滤波器进行相位补偿后，式（8）成为

将式（9）代入式（7）可知，信号通过经相位补偿的滤波器后，时域误差信号关于均方根输入信号能量的相对误差上界为

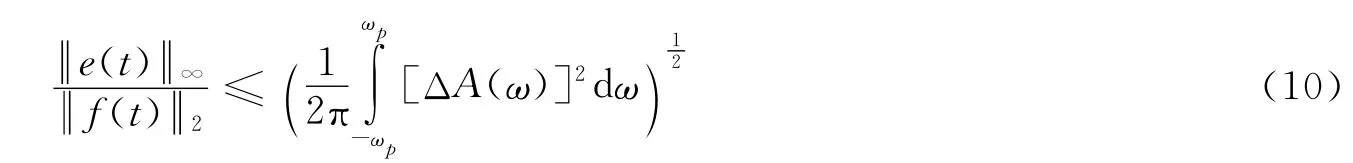
在式（10）中，右端所示的时域误差上界已与滤波器幅度特性相联系。

对于巴特沃斯滤波器，由于只需使用低阶相位补偿网络即可实现很好的相位补偿，因此式（10）给出的时域误差上界具有足够的可靠性，可以据此导出设计指标及相应的设计公式。

2 滤波器设计公式

经典滤波器设计中，总是先求出低通原型，而后再借助频率变换技术得到实际需要的滤波器。巴特沃斯归一化原型低通滤波器的幅度平方特性为

对式（12）右端中的后两项作泰勒级数展开，得到

注意到在低通原型滤波器的通带内，恒有ω＜1，故式（13）中6 N次以上高次项的合成贡献为负，从而有

将式（14）代入式（10），求出右端的积分后得到

再将上式中的频率关于截止频率ωc进行归一化，式（15）成为

引入归一化单位带宽上的输入信号能量E2f：

其均方根为Ef，则时域误差最大值与均方根归一化单位带宽输入信号能量之比为

上式表示的e可适用于不同的输入信号情况，因而是信号通过滤波器后时域误差的一个很好量度，可以据此构建出时域信号误差指标。

将式（16）中的 f（t）2按式（17）所示关系以Ef表示，得到

此即相位补偿巴特沃斯滤波器情况下时域误差信号关于均方根归一化单位带宽输入信号能量的相对误差上界，简称为时域误差上界。

对于给定的时域误差指标emax，根据式（19），显然应有

这样就构建出了以时域误差要求形式出现的滤波器通带要求。

滤波器的阻带要求与经典设计相同［1－2］，仍为

式（21）中，As为阻带衰减，单位为分贝（dB）。式（21）所示的阻带要求也可改写为

从式（20）、（22）中消去ωc，得到

这样，在给定通带频率ωp、阻带频率ωs及时域误差指标emax、阻带衰减指标As后，滤波器的阶次N即可由式（23）求出。尽管式（23）所示的不等式为超越形式，无法求出解析解，但由于所求N值是个正整数，因此稍作试凑就可求出使此式成立的最小N值，也不难编程求取。

在得到滤波器阶次N后，由式（20）和式（22）可得到滤波器的截止频率

这样，式（23）和式（24）就给出了将时域信号误差作为通带指标的巴特沃斯滤波器设计公式。

3 与经典设计方法的比较与示例

现对以上提出的设计方法与经典设计方法作一比较并给出设计示例。由于线性带通系统时域响应的复包络不随频谱搬移而改变［9］，因此最大时域误差也不会因频谱搬移而改变；而在经典滤波器设计中，频率变换技术已完全成熟，因此仅讨论低通滤波器情况。表1给出了两种设计方法的设计参数与指标及设计方程和设计公式。

表1 两种设计方法的设计参数与指标、设计方程和设计公式Table 1 Parameters and specifications，equations and formulas of two design procedures

表1中，经典设计方法的截止频率ωc求取公式与常规所见形式有所不同，这里以不等式方式给出了其取值范围，以便对两种设计方法所得截止频率的异同进行比较。通常，文献中经典设计的ωc求取公式为［1－2］：

这样所得的两个截止频率将分别严格满足通带起伏要求或阻带衰减要求。实际上，稍加分析即可看出，将表1所示不等式中的两个“≤”号分别取为等号，就可得到式（25）和式（26）。还可看出，由于两种设计方法的阻带衰减要求相同，式（26）也适用于本研究提出的方法。

由表1可见，两种方法的设计思路相同，计算复杂度也无实质性差别。从指标系统看，两者的阻带指标完全相同，而笔者提出的方法将时域信号误差指标取为通带指标，从而将时域误差要求直接引入到了经典的模拟滤波器设计之中。注意到在这类应用中，滤波器的主要功能是要对有用信号通过滤波器通带后产生的失真进行控制，因此，将时域误差代替通带起伏作为通带要求应是一个合理的做法。此外，从两者的通带要求表达式（20）和式（26）还可以看出，由于在通带内＜1，因此随着滤波器阶次N的增大，无论是时域误差还是通带起伏都将减小。这就提示了这两种方法具有相容性，也即，如果设计中同时有时域误差指标和通带起伏指标要求，则可用两种方法分别求出滤波器的阶次，取其大者，就可同时满足时域误差指标要求和通带起伏指标要求。下面给出两个设计示例。

例1 低通滤波器要求为：时域误差emax＝0．04，阻带衰减AS＝40dB，ωs＝2ωp。则由式（23）略经试探即可得到N＝7。求出滤波器的阶次后，从式（24）可求出滤波器的截止频率为

取定ωc数值后，再经相位补偿，就完成了滤波器设计。

若将滤波器通带指标由时域误差指标改为通带起伏指标Rp＝2．1dB，其他不变。则由经典设计方法可得N＝7，再由表1所给公式求出滤波器截止频率为

比较两种设计所得结果可以看出，若取N＝7，截止频率ωc＝0．517 95ωs，则在进行相位补偿后，所得的滤波器可同时满足上面给定的时域误差指标和频域中的通带起伏和阻带衰减指标要求。

例2 低通滤波器要求为：时域误差emax＝0．02，通带起伏Rp＝1dB，阻带衰减AS＝50dB，ωs＝2ωp。此例中，在通带内同时存在着时域误差要求和通带起伏要求，因此应结合使用两种设计方法。这时，用笔者的方法根据时域误差要求得到的N＝9，而用经典设计方法根据通带起伏要求得到的N＝10。因此应取N＝10，然后从N＝10出发类似例1分别由表1中设计公式求出相应的截止频率范围，决定出合适的截止频率ωc，再进行相位补偿，就可以完成设计。实际上，实用中只需根据式（26）求出ωc＝0．562 34ωs即可。显然，例2中得到的滤波器在满足频域指标要求的同时，在时域误差性能上已超过了设计要求。不难验证，这一滤波器可满足emax＝0．01的时域误差要求。

这两个示例表明，改进的设计方法弥补了经典滤波器设计不能使用时域误差指标的不足。更有意义的是，在同时存在时域误差与频域通带起伏要求的情况下，可将两种方法结合起来使用以满足设计要求。

4 结 语

对于存在滤波器时域失真性能要求的应用场合，由于经典的滤波器设计方法不能将时域失真要求设置为设计指标，因而无法直接采用。针对这一问题，笔者考察了产生这一困难的原因，探索了可能的解决途径。考察表明，在对滤波器进行相位补偿后，就可以导出时域信号误差的上界并进而据此形成设计指标。在此基础上，笔者就巴特沃斯滤波器提出了一种新的滤波器设计方法，用时域信号误差指标代替了经典设计中的通带起伏指标，并给出了完整的设计公式。比较与示例分析表明，此设计方法与经典设计方法的算法难度基本相同，且完全相容。因此，将两种设计方法结合，就可适用于同时存在通带起伏要求和时域误差要求的应用场合。此外，虽然笔者仅就巴特沃斯滤波器进行了探索，但从文中分析可见，所提出方法在原理上也可适用于经相位补偿后的其他滤波器形式。

［1］ Chen W K．The Circuits and Filters Handbook［M］．2ed．Boca Raton：CRC Press，2002．

［2］ Paarmann L D．Design and Analysis of Analog Filters：A Signal Processing Perspective with MATLAB Example［M］．New York，Boston，Dordrecht，London，Moskow：ebook，2003：259－265．

［3］ Aleksandar L，Sasa D，Mladen V．Time－domain synthesis of linear－phase selective filters［C］／／MIPRO，2010 Proceedings of the 33rdInternational Convention．Opatija：IEEE，2010：165－170．

［4］ Bau N，Seara R，Bermudez J C M．Design of IIR digital filters from time－domain specifications［C］／／IEEE International Sympoisum on Circuits and Systems．Singapore：IEEE，1991，5：2443－2446．

［5］ Piskorowski J．Phase－compensated time－varing butterworth filter［J］．Analog Integrated Circuits and Signal Processing，2006，47（2）：233－241．

［6］ Piskorowski J，Kaszynski R．A novel concept of phase－compensated continuous－time filter［J］．Analog Integrated Circuits and Signal Processing，2007，51（1）：39－44．

［7］ Piskorowski J．A new concept of phase－compensated continuous－time Chebyshev filters［J］．Signal Processing，2008，88（3）：437－447．

［8］ Jain R K，Pande D C．Filter design technique for improving time domain fidelity of data line filter［C］／／Proceedings of the 8th International Conference on Electromagnetic Interference and Compatibility．Bangalore：IEEE，2003：37－40．

［9］ Proakis J G．Digital Communications［M］．New York：McGraw Hill，1983：105－136．