基于纯方位角测量的水下目标被动跟踪技术

宋绪栋, 蔚 婧, 李晓花, 李亚安



基于纯方位角测量的水下目标被动跟踪技术

宋绪栋1, 蔚 婧2, 李晓花2, 李亚安2

(1 中国人民解放军91388部队, 广东 湛江, 524022; 2. 西北工业大学 航海学院, 陕西 西安, 710072)

水下目标的被动跟踪技术在军事上具有重要的应用价值, 为了解决基于纯方位角测量的水下目标被动跟踪技术在实际应用中的问题, 研究了几种适合于单、双观测站的水下目标被动跟踪算法。分别对伪线性估计算法、扩展卡尔曼滤波算法、无迹卡尔曼滤波算法在不同参数情况下的性能进行了详细的仿真与分析。仿真结果表明, 静止单观测站虽不能获得目标的完全观测, 但是在具有一定先验信息的情况下, 伪线性估计算法也可以实现对目标轨迹的估计; 双观测站可以获得对目标的完全观测, 并且在观测方程严重非线性的情况下, 无迹卡尔曼滤波方法的性能要优于扩展卡尔曼滤波方法。仿真结果对工程应用具有重要的参考价值。

水下目标; 纯方位目标跟踪; 伪线性估计; 扩展卡尔曼滤波; 无迹卡尔曼滤波

0 引言

根据跟踪系统获得量测数据的方式不同, 目标跟踪可以分为主动式与被动式[1]。主动式跟踪主要由主动雷达或声纳获取目标相对于观测器之间的距离和相对方位角。这种观测方式跟踪目标精确, 处理速度快, 但往往由于自身向外发射信号, 因而很容易被敌方获知观测器的具体位置, 在军事上具有很大劣势[2]。被动式跟踪一般由被动雷达、声纳或者通过红外来获得目标相对于观测器之间的方位角, 通过解算而获得目标的状态值。这种观测方式由于是被动的接收信号, 因此具有很强的隐蔽性, 但由于观测量的减少导致目标的跟踪精度和收敛程度都有所降低, 这种跟踪方式应用于军事领域, 往往能够给予敌方目标出其不意的毁灭性打击[3]。

水下目标的被动定位和跟踪技术源于鱼雷、潜艇等武器的隐蔽进攻, 通过被动传感器测量到的目标信息确定目标的运动参数, 如位置、速度和加速度等。这种方式对鱼雷、潜艇等自主式攻击性武器来说极其重要。

近年来, 基于纯方位角测量的水下目标跟踪问题一直是研究的热点和难点, 目前常用的方法有多种, 如伪线性估计器[4](pseudo-linear estimator, PLE), 扩展卡尔曼滤波(extended Kalman filter, EKF), 无迹卡尔曼滤波(unscented Kalman filter, UKF)等。本文从实际工程应用的角度出发, 针对单观测站和双观测站两种情况, 对以上几种可行方案进行了详细分析, 通过仿真试验得出各种方案在不同应用环境下的优劣, 旨在为下一步工程应用提供参考。

1 系统模型

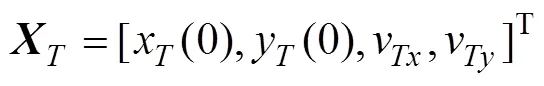
图1 目标与观测站的几何关系示意图

Fig. 1 Geometric relationship of sonar systems and target

2 单站纯方位伪线性估计算法

对纯方位目标跟踪问题的大量研究表明, 利用静止单站所测量的目标方位信息, 不可能同时解算出目标的距离、航向及速度等全部参数, 即由于存在“距离模糊”, 系统是不完全可观测的[5]。但是, 在目前实际的军事应用中, 传感器网络还没有建立的情况下, 不能同时利用多个观测站对目标进行跟踪, 因此, 基于单观测站的纯方位目标跟踪方法肩负着极其重要的责任。若进一步对目标具有一定的先验知识, 如通过前期目标识别已经知道目标的型号及速度, 则可通过先验知识对目标参数进行解算, 实现完全观测。

对式(3)作拟线性处理, 得

定义

可得伪测量方程

对于静止或者非机动单站, 虽然不能实现对目标的完全观测, 但是可以获得目标的航向, 以及目标与观测站的初始距离与目标速度的比值。这在工程实践中也具有重要的实际意义, 在对目标速度有一定先验知识的情况下, 即可获得对目标的粗略跟踪, 实现进行隐蔽打击的目的。

3 双站纯方位目标跟踪方法

对于匀速直线运动的目标, 利用多个被动传感器组成传感器网络能在较广泛的区域内实现对目标的角度跟踪, 配合适当的信息融合算法, 可以实现对目标的完全观测。这里将以比较实际的双观测站为例进行分析。

3.1 扩展卡尔曼滤波方法

在模型满足高斯线性条件下, 典型的卡尔曼滤波可获得线性无偏的最小方差估计[6-7]。但是在实际应用中, 线性、高斯等假设条件常常不能满足要求, 出现滤波精度下降和发散的现象。EKF就是为了克服状态方程的非线性问题, 将其在状态的滤波值附近进行泰勒级数展开, 得到线性化后的状态方程, 进而采用卡尔曼滤波方法进行处理。

假设系统模型可表示为

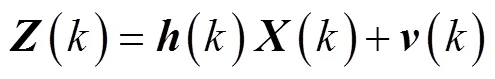
EKF方法是解决非线性滤波问题比较经典的方法, 但是由于弱可观测条件下测量模型的非线性, 可能会产生滤波过程的发散现象。

3.2 无迹卡尔曼滤波方法

为了改善非线性问题的滤波效果, Julier等人提出了采用UKF方法对非线性问题进行滤波估计[8-10]。该方法在处理状态方程时, 首先进行无迹变换, 然后使用变换后的状态变量进行滤波, 以减小估计误差。其滤波效果在复杂的非线性系统下, 要明显优于EKF。

离散非线性系统可以描述为

该方法的简要步骤如下。

2) 计算权值

3) 计算sigma采样点的状态向量

4) 时间更新

5) 量测更新

在UKF算法中, 最重要的问题是确定sigma点采样策略, 也就是确定sigma采样的个数、位置及相应的权值。目前已有的采样策略有对称采样, 最小偏度单形采样, 超球体单形采样等[11]。

4 仿真结果与分析

为了更加细致地分析上述几种方法在不同场合的性能, 本节进行了大量计算机仿真, 旨在通过试验得出一般性规律, 为今后的工程实际应用提供必要的参考。

4.1 静止单站情况(试验1)

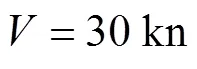
由于基于纯方位信息的静止单站无法获得对目标的完全观测, 因此, 仿真给出了目标的初始距离与目标速度的比值。

图2中实线表示真实值, 虚线表示估计值, 圆圈为观测站位置。目标的航迹图中, 虚线为具有目标先验速度的情况下, 对目标航迹的估计。图3给出了单站静止PLE方法的估计误差。

4.2 静止双站情况(试验2)

试验参数: 运动目标参数同试验1, 2个观测站分别位于(0, 0), (0, 500)。

图4中, 2个圆圈表示2个静止观测站的位置, 实线为目标真实轨迹, 虚线表示EKF方法估计所得目标轨迹, 点划线表示UKF方法估计所得目标轨迹, 这2条曲线基本重合。

图5为所估计各参数分量与真实值之间的误差, 表1给出了其估计方差。

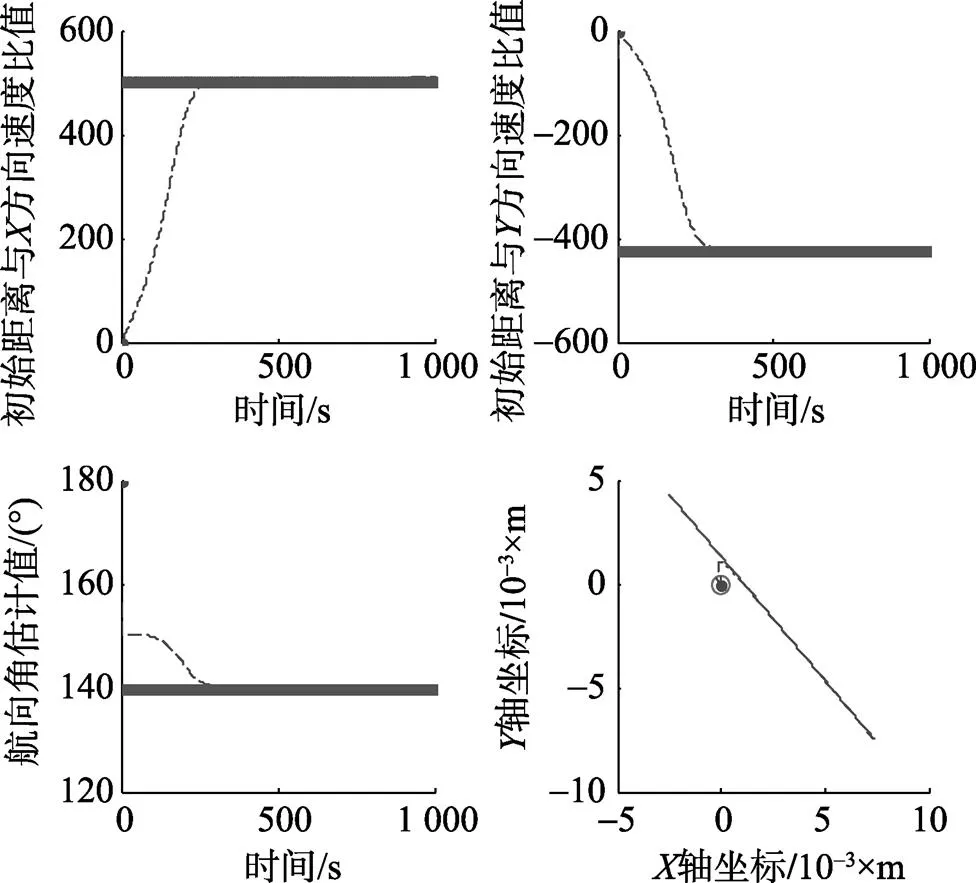
图2 单站静止PLE方法估计结果

图3 单站静止PLE方法估计误差

图4 双观测站静止时UKF与EKF目标轨迹估计

图5 双观测站静止时UKF与EKF估计误差

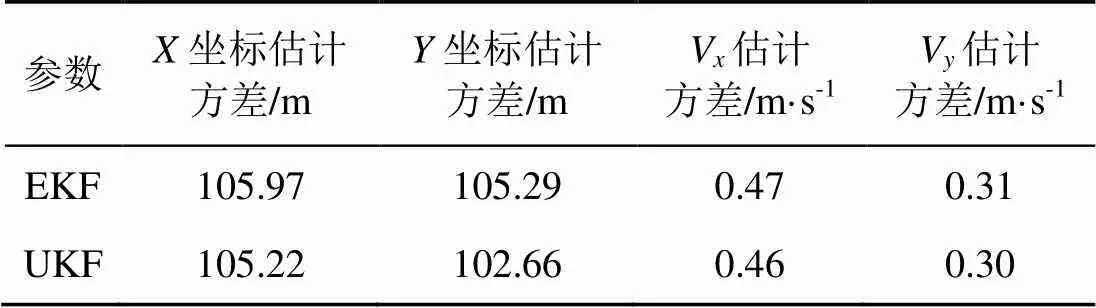
表1 双观测站静止时EKF与UKF方法估计方差

4.3 运动双站情况(试验3)

试验参数: 运动目标参数同试验1, 2个观测站分别位于(0, 0), (0, 500), 2个观测站均以10 kn的速度沿轴正向运动。

图6中, 2个圆圈表示2个观测站的初始位置, 实线为目标真实轨迹。与图4相似, UKF(点划线)和EKF(虚线)这2种方法估计得到的目标轨迹基本重合。图7给出了所估计各参数分量与真实值之间的误差, 表2给出了其估计方差。可以看出, UKF方法的方差要小于EKF方法的方差。

图6 双观测站运动时UKF与EKF目标轨迹估计

图7 双观测站运动时UKF与EKF估计误差

表2 双观测站运动时EKF与UKF方法估计方差

5 结束语

基于纯方位角测量的水下目标被动跟踪方法在军事上具有重要的应用价值, 研究了3种便于工程实用的方法: PLE方法、EKF方法和UKF方法。其中, PLE方法具有计算简单, 无需初值的优点, 在目标不可完全观测的情况下, 它可以获得目标初始距离与速度的比值, 在具有速度先验知识的情况下, 也可以实现对目标轨迹的估计。双观测站可以实现对目标的完全观测, 分别对双观测站静止和运动2种情况进行了仿真分析, 结果表明, EKF方法和UKF方法均能较准确地估计目标轨迹, 并且UKF方法性能要略优于EKF方法。仿真结果对工程实际应用具有一定的参考价值。

[1] 严卫生, 高磊, 张礴, 等. 水下目标跟踪技术[J]. 火力与指挥控制, 2000, 25(2): 2-6.

Yan Wei-sheng, Gao Lei, Zhang Bo, et al. Underwater Target Tracking[J]. Fire Control & Command Control, 2000, 25 (2): 2-6.

[2] 周宏仁, 敬忠良, 王培德. 机动目标跟踪[M]. 北京: 国防工业出版社, 1991.

[3] Song T L. Observability of Target Tracking with Bearing-only Measurements[J]. IEEE Transactions on Aerospace and Electronics Systems, 1996, 32(4): 1468-1471.

[4] Aidala V J. Kalman Filter Behavior in Bearings-only Tracking Applications[J]. IEEE Transactions on Aerospace and Electronics Systems, 1979, 15(1): 29-39.

[5] 孙仲康, 周一宇, 何黎星. 单基地有源无源定位技术[M]. 1版. 北京: 国防工业出版社, 1996.

[6] Konrad R, Rolf U. The Extended Kalman Filter as an Exponential Observer for Nonlinear Systems[J]. IEEE Transactions on Signal Processing, 1999, 47(8): 2324-2328.

[7] Simon J J, Jeffrey K U. A New Method for the Nonlinear Transformation of Means and Covariances in Filters and Estimators[J]. IEEE Transactions on Automatic Control, 2000, 45(3): 477-482.

[8] Dini D H, Mandic D P, Julier S J. A Widely Linear Complex Unscented Kalman Filter[J]. Signal Processing Letters, 2011, 18(11): 623-626.

[9] 高剑, 徐德民, 严卫生, 等. 无迹卡尔曼滤波及其在三维水下目标跟踪系统中的应用[J]. 船舶工程, 2005, 27(3): 24-28. Gao Jian, Xu De-min, Yan Wei-sheng, et al. UKF and Its Application to 3-D Underwater Target Tracking System[J]. Ship Engineering, 2005, 27(3): 24-28.

[10] Valverde G, Terzija V. Unscented Kalman Filter for Power System Dynamic State Estimation[J]. IET Generation, Tran- smission & Distribution, 2011, 5(1)：29-37.

[11] 杨峰, 潘泉, 梁彦, 等. 多源信息空间配准中的UT变换采样策略研究[J]. 系统仿真学报, 2006, 18(3):15-20. Yang Feng, Pan Quan, Liang Yan, et al. Research on Sampling Strategies of UT Transformation for Space Alignment of Distributed Multi-sensor Information[J]. Journal of System Simulation, 2006, 18(3): 15-20.

Passive Underwater Target Tracking Based on Bearings-Only Angle Measurement

SONG Xu-dong1, YU Jing2, LI Xiao-hua2, LI Ya-an2

(1.91338thUnit, The people′s Liberation Army of China, Zhanjiang 524022, China; 2. College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China )

In regard to actual application of passive underwater target tracking technology based on bearings-only angle measurement, several algorithms for monostatic and bistatic sonar systems, i.e. the pseudo-linear estimation (PLE), the extended Kalman filter (EKF), and the unscented Kalman filter (UKF), are discussed, and their performances are simulated with different parameters, respectively. Simulation results illustrate that: 1) The nonmoving monostatic sonar system can not obtain all-around observation of target, but when prior information of the target velocity is available the trajectory of the target can be acquired by using the PLE algorithm; 2) The bistatic sonar system can achieve all-around observation of target, and the performance of the UKF is better than that of the EKF when the observation equation is very nonlinear.

underwater target; bearings-only target tracking; pseudo-linear estimation(PLE); extended Kalman filter(EKF); unscented Kalman filter(UKF)

TJ630.34;TN953

A

1673-1948(2012)05-0353-06

2012-01-06;

2012-04-19.

国家自然科学基金资助项目(51179158).

宋绪栋(1968-), 男, 高级工程师, 主要从事鱼雷靶标总体技术研究.

(责任编辑: 杨力军)