联合对角化技术在空间谱估计中的应用

赵龙龙, 宋海岩



联合对角化技术在空间谱估计中的应用

赵龙龙1, 宋海岩2

(1. 中国人民解放军91388部队, 广东 湛江, 524022; 2. 黑龙江工程学院 电气与信息工程学院, 黑龙江 哈尔滨, 150050)

在实际工程应用中, 传统空间谱估计方法受噪声、干扰及采样效应等因素影响, 其性能明显退化。为了克服这些因素对方位估计结果的影响, 提高算法性能, 本文将空时相关矩阵组代替传统的采样协方差矩阵, 利用联合对角化这一新的数学工具, 研究了一种基于Jacobi旋转正交联合对角化的空间谱估计方法。通过对空时相关矩阵组进行联合对角化, 得到了联合对角化矩阵和对角化后的矩阵组, 最终利用联合特征值和特征向量得到修正的阵列协方差矩阵, 并对空间谱估计处理器进行修正。仿真结果表明, 在不同的信噪比、快拍数等条件下, 基于联合对角化的空间谱估计算法较传统方法具有更高的分辨力和更低的均方根误差, 能有效降低方位估计的信噪比门限, 进而改善传统空间谱估计方法的方位估计性能。

空间谱; 联合对角化; Jacobi旋转; 空时相关矩阵组; 方位估计

0 引言

随着电子信息科学的迅猛发展, 空间谱估计技术作为信号处理的一个重要分支, 在国民经济及国防建设中发挥了重要作用, 并广泛应用于声纳、雷达、医学等研究领域, 引起了广大研究者的高度重视[1]。最早, Burg将熵的概念推广到空间谱估计领域, 由于该算法突破了瑞利限的限制, 吸引了广大研究者对现代谱分析参数模型法进行广泛研究[2]。其后, Capon提出了最小方差法(standard capon beamforming, SCB), 该方法可在保持来波方向信号能量不变的前提下, 使波束内其他方向的能量最小化, 同时获得较高的分辨力以及较强噪声干扰抑制能力[3]。20世纪80年代后期, Schmidt等人提出了多重信号分类(multiple signal classification, MUSIC)算法[4], 引起人们对子空间类算法的广泛兴趣, 促进了子空间类算法的兴起, 开启了高分辨空间谱估计技术的新纪元。20世纪90年代以来, 高分辨阵列处理与优化理论、信息论等相关学科密切结合, 出现了很多新的算法和理论。主要包括波束域高分辨阵列信号处理[5-6]、宽带信号空间谱估计[7-8]、循环平稳信号的空间谱估计[9-10]以及基于高阶累积量的空间谱估计[11-12]等。

然而, 在实际工程应用中, 高分辨空间谱估计方法的性能在很大程度上受信噪比、采样效应等因素的影响。如何克服或消除这些因素的影响, 是制约高分辨算法走向工程实用化的关键。

针对这一问题, 本文从基阵接收信号的2阶统计特性出发, 采用Jacobi旋转正交联合对角化技术, 对空时相关矩阵组进行联合对角化处理。该方法通过构造合适的联合对角化结构, 进而对高分辨处理器进行修正, 能够有效抑制噪声及干扰的影响, 改善高分辨空间谱估计方法在实际工程应用中的性能。

1 空时相关矩阵联合对角化结构

进一步对导向矢量矩阵进行奇异值分解得到

代入式(2)中可得到

将式(4)的联合对角化问题简写为以下的数学表达式, 从而可以用数学方法解决空间谱估计问题

2 基于Jacobi旋转的空时相关矩阵联合对角化

可证明, 联合对角化问题等价于求解以下的约束最大化问题[17]

应用基于Jacobi旋转的正交联合对角化方法对进行求解, 可将矩阵组的联合对角化问题转化为一系列Jacobi旋转。最终可表示为一系列Jacobi旋转矩阵乘积的形式。由于联合对角化矩阵中同时包含了信号子空间和噪声子空间的全部信息, 因此可以同时利用和进行方位估计。

空时相关矩阵的联合特征值估计结果为

得到修正后的联合对角化SCB空间谱表示为

为讨论方便, 将基于2阶累积量联合对角化的方位估计方法(joint diagonalization conventional beamforming based on second cumulant, JDCB-SC)。综上所述, JDCB-SC方位估计方法的信号处理流程见图1。

图1 JDCB-SC算法的信号处理流程图

3 仿真结果与分析

仿真条件1: 考察对空间方位角靠得很近的双相干声源的分辨能力。

图2 空间谱估计结果

仿真条件2: 不同信噪比条件下的双相干源方位估计精度。

图3 不同信噪比下的双相干源方位估计均方根误差

从图3可看出, 传统SCB方法的RMSEs曲线总体上要高于JDCB-SC方法, 特别是在信噪比为-2 ~11 dB这一变化区间。当信噪比小于5 dB时, SCB方法的RMSEs始终较高, 保持5°左右; 而JDCB-SC方法随着信噪比的减小, RMSEs逐渐增大, 在信噪比约为0 dB时, RMSEs约为2°。当信噪比大于5 dB时, 2种方法的RMSEs都逐渐减小, 而JDCB-SC方法的RMSEs始终较低, 不超过0.2°, 相比之下SCB方法的RMSEs在信噪比约为10 dB时, RMSEs仍保持0.3°。综上所述, 在相同信噪比条件下, JDCB-SC算法较SCB算法具有较低的方位估计RMSEs, 提高了算法的估计精度。

仿真条件3: 不同快拍数下的双相干源方位估计精度。

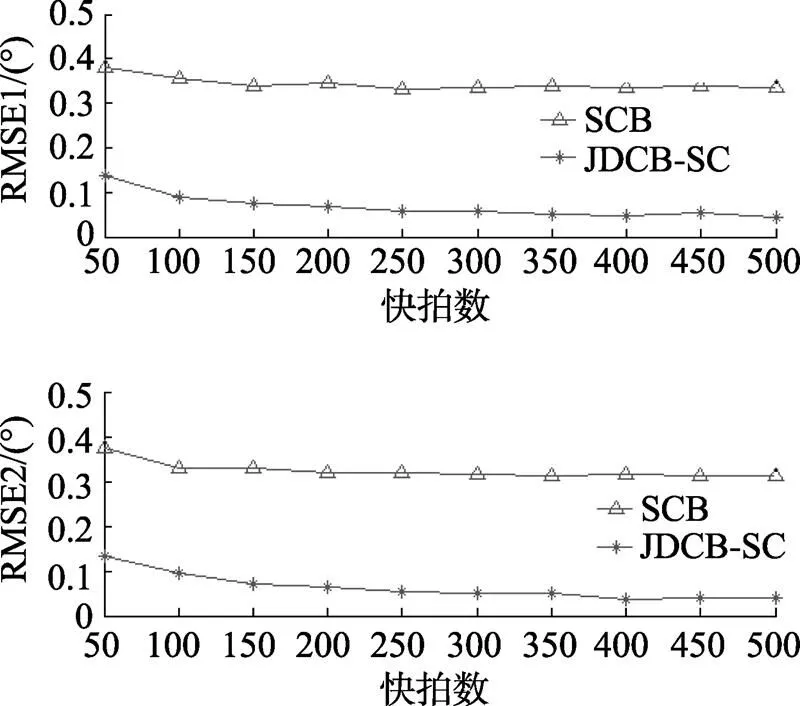
图4 不同快拍数下的双相干源方位估计均方根误差

从图4中可以看出, 随着采样快拍数的增加, SCB和JDCB-SC方法估计目标方位的RMSEs均有所下降, 即在大快拍数条件下, 2种方法的性能均有所改善。在整个快拍数变化的区域中, JDCB-SC方法的RMSEs始终要低于SCB方法的, 两者相差约为0.25°。综上所述, 在相同的采样快拍数条件下, JDCB-SC算法较SCB算法具有较低的方位估计RMSEs, 提高了算法的估计精度。

4 结束语

本文从基阵接收信号的2阶统计特性角度出发, 通过Jacobi旋转正交联合对角化方法, 构造空时相关矩阵组联合对角化结构, 重新获得了联合特征值并对空间谱进行修正。仿真结果表明, 该方法能够有效提高常规空间谱估计算法在噪声、有限采样效应下的方位估计性能, 具有更高的空间分辨能力及更低的目标方位估计均方根误差。

[1] 王永良, 陈辉, 彭应宁, 等. 空间谱估计理论与算法[M]. 北京: 清华大学出版社, 2004.

[2] Krim H, Viberg M. Two Decades of Array Signal Processing Research[J]. IEEE Signal Processing Magazine, 1996, 13(4): 67-94.

[3] Capon J. High-resolution Frequency-wave Number Spectrum Analysis[J]. Processing of the IEEE, 1969, 57(8): 1408-1418.

[4] Schmidt R O. Multiple Emitter Location and Signal Parame- ter Estimation[J]. IEEE Transaction, 1986, AP-34(3): 276- 280.

[5] Zoltowski M D. High Resolution Sensor Array Signal Pro- cessing in the Beamspace Domain: Novel Techniques Based on the Poor Resolution of Fourier Beamforming[C]//In Proc. Fourth ASSP Workshop Spectrum Estimation Modeling，1988, 8(1): 350-355.

[6] Xu X L, Buckley K M. Reduced-dirmension Beamspace Broadband Source Localization: Preprocessor Design and Evaluation[J]. In Proc. Fourth ASSP Workshop Spectrum estimation Modeling, 1988, 8(1): 22-27.

[7] Wang H, Kaveh M. Estimation of Angles-of-arrival for Wideband Sources[J]. ICASSP, 1984, 9(1): 279-282.

[8] Hung H, Kaveh M. Focusing Matrices for Coherent Sign- al-subspace Processing[J]. IEEE Transaction on ASSP, 1988, 36(8): 1272-1281.

[9] Gardner W A. Exploitation of Spectral Redundancy on Cycl- ostationary Signals[J]. IEEE Transactions Signal Processing Magazine, 1991, 8(4): 14-37.

[10] Xu G, Kailath T. Direction-of-Arrival Estimation via Explo- itation of Cyclostationarity-A Combination of Temporal and Spatial Processing[J]. IEEE Transactions on SP, 1992, 40(7): 1775-1785.

[11] Leyman A R, Durrani T S. Signal Subspace Processing Using Higher Order Statistics[J]. Electronics Letters, 1994, 30(16): 1282-1284.

[12] Leyman A R, Durrani T S. Signal Subspace Techniques for DOA Estimation Using Higher Order Statistics[J]. ICASSP, 1995, 3(1): 1956-1959.

[13] Belouchrani A, Amin M G, Abed-Meraim K. Direction Finding in Correlated Noise Fields Based on Joint Block Diagonalization of Spatio-Temporal Correlation Matrices[J]. IEEE Signal Processing Letters, 1997, 4(9): 266-269.

[14] 蒋飚, 朱埜, 孙长瑜. 基于空时相关阵联合对角化的高分辨方位估计. 哈尔滨工程大学学报. 2005, 26(6): 773-776. Jiang Biao, Zhu Ye, Sun Chang-yu. High-resolution Direction Finding Based on Joint Block-diagonalization of Spatio- temporal Correlation Matrice[J]. Journal of Harbin Engin- eering University. 2005, 26(6): 773-776.

[15] 蒋飚. 基于空时相关阵联合对角化的子空间DOA估计. 声学与电子工程[J]. 2006, 27(Z): 1-3.

[16] 宋海岩, 朴胜春. 基于高阶累积量矩阵组正交联合对角化的高分辨方位估计方法[J]. 电子与信息学报. 2010, 32(4): 967-972. Song Hai-yan, Piao Sheng-chun. DOA Estimation Method Based on Orthogonal Joint Diagonalization of High-order Cumulant[J]. Journal of Electronics & Information Tech- nology. 2010, 32(4): 967-972.

[17] Cardoso J F, Souloumiac A. Jacobi Angles for Simultaneous Diagonalization[J]. SIAM J Mat Anal, 1996, 17(1): 161-163.

Application of Joint Diagonalization Technology to Spatial Specturm Estimation

ZHAO Long-long1, SONG Hai-yan2

(1.91388thUnit, The people′s Liberation Army of China, Zhanjiang 524022, China；2. College of Electrical and Information Engineering, Heilongjiang Institute of Technology, Harbin 150050, China )

In practical engineering applications, the performance of conventional spatial spectrum estimation method gets degraded due to the effects of noise, interference and sampling effect, etc. In order to reduce these effects on direction of arrival (DOA) estimation, this paper uses the joint diagonalization to construct the joint diagonalization structure of the spatial-time correlation matrix groups, and obtains a spatial spectrum estimation method based on Jacobi rotation orthogonal joint diagonalization. Thus, corresponding eigenvalues and eigenvectors are utilized to obtain the revised covariance matrix, and the spatial spectrum estimator is revised. Simulation results show that, under different signal to noise ratio(SNR) and snapshots, the proposed method can significantly improve the DOA estimation performance of the conventional spatial spectrum estimation method.

spatial spectrum; joint diagonalization; Jacobi rotation; space-time correlation matrix groups; direction of arrival(DOA) estimation

TJ630.34; TB556

A

1673-1948(2012)05-0344-04

2012-03-13;

2012-04-01.

赵龙龙(1976-), 男, 硕士, 工程师, 研究方向为水声工程.

(责任编辑: 杨力军)