简支T梁损伤识别方法的研究

王 吉

(重庆交通大学土木建筑学院，重庆 400074)

早期单一用于损伤识别指标的振动模态参数(固有频率，振型，阻尼)，由于在实际方法应用上很多的局限性，已经很少采用。当前对结构的损伤识别研究的方法中，基于模态响应的柔度曲率差和基于移动荷载下动态响应的二阶导数差，这两种手段在实际的应用中比较常见。采用分析了不同损伤工况下，柔度曲率差和动态响应的二阶导数差的变化规律，发现柔度曲率差和二阶导数差对损伤的灵敏度不同，单独用一种方法不能很好地识别，可以考虑采用两种指标结合考虑。

1 柔度曲率差理论

利用依据模态理论的相关分析，可求出柔度矩阵:

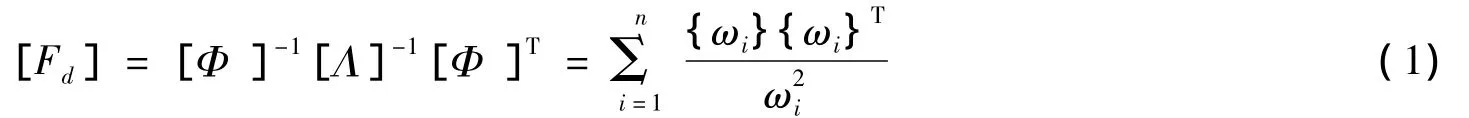
式(1)中{φi}为质量矩阵归一化的第i阶列阵，wi为结构的第i阶模态频率，n为结构的模态阶数。从式(1)中，可以看出，柔度矩阵Fd与频率成反比，高阶对柔度矩阵的影响越来越小，因此只需测量低阶振型和频率，就满足精度要求。

将结构损伤前的柔度矩阵记为［Fu］，结构损伤后的柔度矩阵记为［Fd］。则柔度矩阵改变量可表示:

取柔度差ΔF矩阵中的主对角元素生成的列向量{Δq}，即

利用差分公式计算曲率公式:fi-1，fi，fi+1分别为节点i-1，i，i+1 号节点的柔度值，f″i为i节点的曲率。利用式(4)计算出{Δq}，曲率差向量{Δf″}。当结构某局部位置发生损伤时，即该位置的曲率差会产生突变。

2 动态响应二阶导数差理论

在匀速移动常量力荷载作用下，简支梁的振动方程:

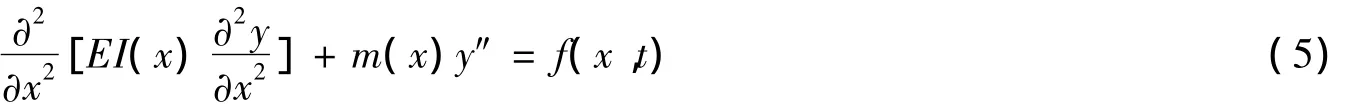
式(5)中m(x)为梁质量，E为弹模，I为惯性矩，f(x，t)为梁上激励力，y(x，t)为梁上动力响应值。

根据模态分析得相关理论，得出:

式(6)中的y(x，t)为移动荷载作用下，在竖向的动力影响值，φn为模态振型。

在移动荷载作用下各节点振动的竖向值得二阶导数:

通过二阶导数差会产生突变Δy″i，即损伤前后的二阶导数差值，来判别结构的损伤情况。

3 混凝土简支T梁算例

有一跨径6 m的混凝土简支T梁，弹性模量E=30 GPa，泊松比0.166 7，质量密度为2 600 km/m3，在ANSYS中利用beam44单元建立模型，建立20个节点，19个单元。

利用刚度折减的方法，来模拟损伤的程度。(1)工况1:全桥处于正常状态，无损伤。(2)工况2:全桥1/4位置损伤50%，其余全桥处于正常状态。(3)工况3:全桥跨中位置损伤50%，其余全桥处于正常状态。(4)工况4:全桥1/4位置、跨中位置都损伤50%，其余全桥处于正常状态。

3.1 工况2的损伤分析

图1为在工况2下，全桥的柔度曲率差曲线。图2为工况2下，全桥的动态响应的二阶导数差曲线。从图1和图2，都可以发现1/4位置附近曲线突变，说明两种指标都能识别出结构损伤的位置。另外，图1除突起的位置外，图形比较光滑，图2在起点到1/4跨径之间位置也有一定的突变，说明在识别损伤的具体位置时，柔度曲率差更精确。同时可以发现损伤位置对未损伤位置的二阶导数差影响有点大，说明动态响应的二阶导数差比柔度曲率差对损伤程度更敏感。

3.2 工况3的损伤分析

图3为在工况3下，全桥的柔度曲率差曲线。图4为工况3下，全桥的动态响应的二阶导数差曲线。从图3和图4，都可以发现跨中位置附近曲线突变，说明两种指标都能识别出结构损伤的位置。另外，图3除突起的位置外，图形比较光滑，图4在其余位置也有少量的突变，特别在1/4位置到跨中之间和跨中到3/4位置之间尤其明显，说明在识别损伤的具体位置时，柔度曲率差更精确。同时可以发现损伤位置对未损伤位置的二阶导数差影响有点大，说明动态响应的二阶导数差比柔度曲率差对损伤程度更敏感。

3.3 工况4的损伤分析

图5为在工况4下，全桥的柔度曲率差曲线。图6为工况4下，全桥的动态响应的二阶导数差曲线。从图3和图4，都可以发现1/4位置、跨中位置附近曲线突变，说明两种指标都能识别出结构损伤的位置。从图5中可以看出在1/4位置处的突变没有跨中位置处效果明显。图6却在1/4位置处的突变效果比图3明显。说明二阶导数差在识别多处损伤的程度比柔度曲率差的效果好。另外，同样与前面两种工况相同，图6其他位置的突变比较明显，说明在损伤位置对未损伤的位置影响程度方面，动态响应的二阶导数差比柔度曲率差更敏感。

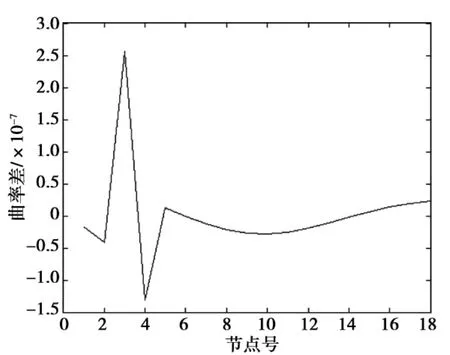
图1 工况2柔度曲率差曲线

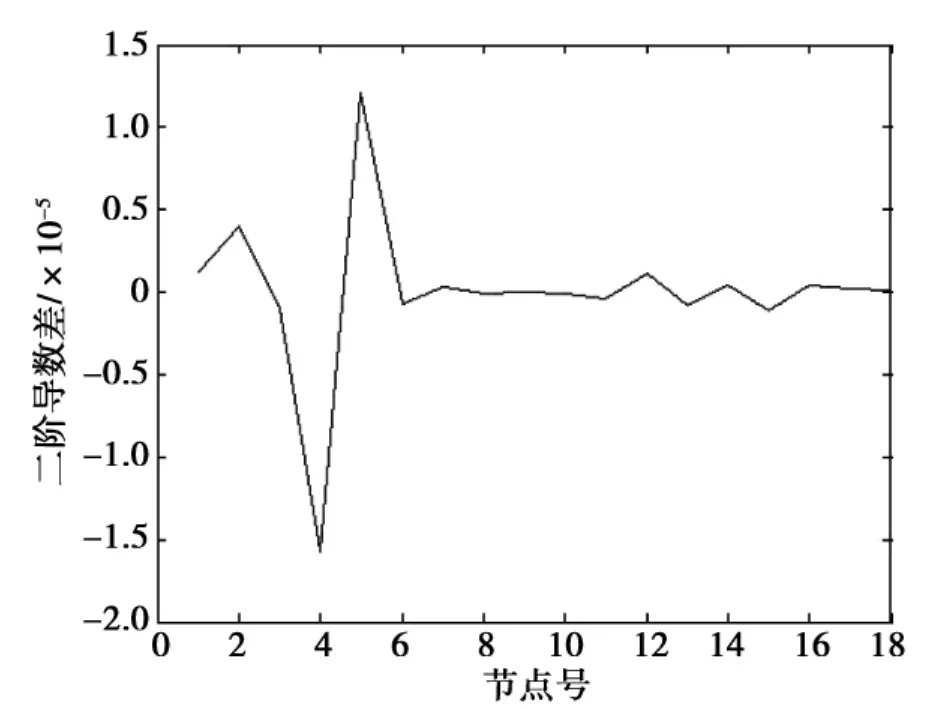
图2 工况2二阶导数差曲线

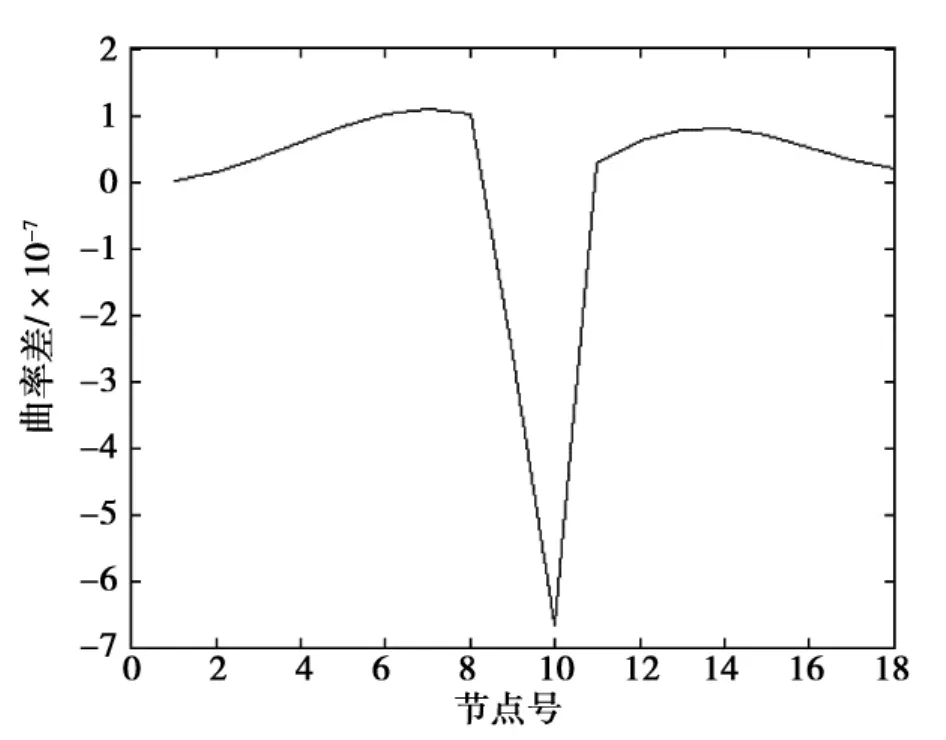
图3 工况3柔度曲率差曲线

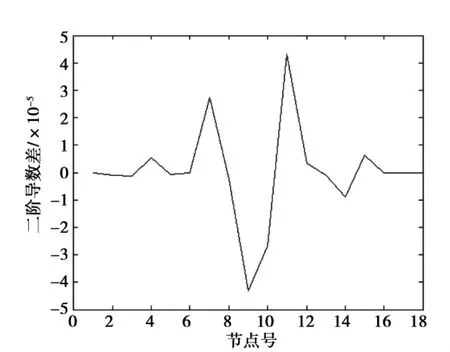
图4 工况3二阶导数差曲线

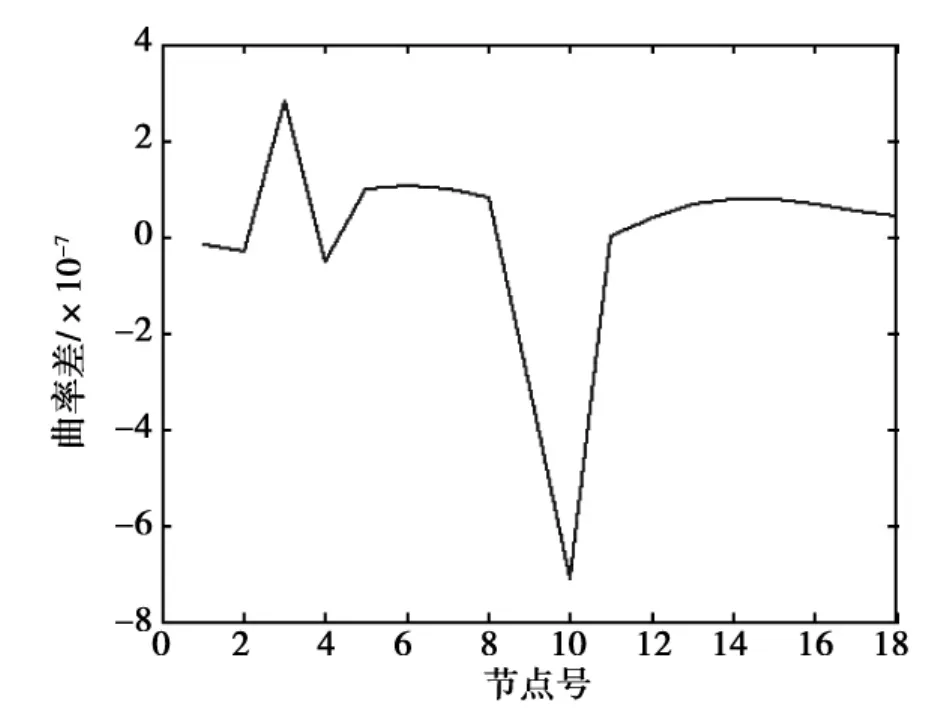
图5 工况4柔度曲率差曲线

图6 工况4二阶导数差曲差

4 结语

通过上述的有限元的分析，可以发现对结构进行损伤识别时，用柔度曲率差和动态响应二阶导数差两种方法，对损伤的程度和灵敏度有一些不同。对损伤位置的准确识别时，柔度曲率差比动态响应二阶导数差更方便，更精确。在损伤位置对未损伤位置的影响程度方面，动态响应二阶导数差识别更灵敏。柔度曲率差，是基于模态的基础上的，虽然精度上符合要求，但是忽略了高阶模态的影响，有一定的误差。动态响应二阶导数差，也有一些缺点，比如受移动速度，移动位移的影响比较大，对结果产生一定的影响。将上述两种方法联合起来使用，可以在一定程度上弥补各自不足，可以更加准确地识别检测结构的损伤情况。

［1］李德葆，陆秋海.实验模态分析及其应用［M］.北京:科学出版社，2001

［2］肖剑强.曲率模态和柔度曲率对损伤的敏感性研究［J］.兰州交通大学学报:自然科学版，2007，26(1):78-81

［3］常军，白羽.钢筋混凝土梁的损伤识别方法研究［J］.昆明理工大学学报:理工版，2003，28(1):105-107

［4］曹水东，李传习，徐飞鸿，等.基于结构柔度矩阵损伤识别的柔度曲率比法［J］.长沙电力学院学报:自然科学版，2006，21(1):85-88

［5］王新敏.ANSYS工程结构数值分析［M］.北京:人民交通出版社，2007

［6］薛松涛，钱宇音，陈镕，等.采用二阶频率灵敏度的损伤识别和试验［J］.同济大学学报，2003，31(3):263-267

［7］PANDEY A，BISWAS M.Damage detection in structures using changes in flexibility［J］.Journal of Sound and Vibration，1994，169(1):3-17