分位数回归与局部线性回归的估计的稳健性比较研究

王秀文，王景旭

(1．温州大学数学与信息科学学院，浙江温州 325035；

2．华中农业大学经济管理学院，湖北武汉 430000)

分位数回归与局部线性回归的估计的稳健性比较研究

王秀文1，王景旭2

(1．温州大学数学与信息科学学院，浙江温州 325035；

2．华中农业大学经济管理学院，湖北武汉 430000)

在介绍分位数回归估计方法理论和局部线性回归估计方法理论的基础上，分别建立模型分析了2008 – 2011年我国通货膨胀和海关进出口总额之间的关系，结果表明：分位数回归估计方法具有更加稳健的特点；在研究通货膨胀和海关进出口总额之间关系时，使用分位数回归模型更加有效．

分位数回归；局部线性回归；通货膨胀；海关进出口总额；稳健性

分位数回归自提出以来在经济、金融、医学、教育等领域得到了广泛的应用，它本身属于一种半参数回归估计的方法，而且它的稳健性在理论上和应用方面都得到了证实．但是，有关其稳健性与其他估计方法比较的研究还相对较少，本文用分位数回归估计的方法与局部线性回归估计的方法分析了2008 – 2011年我国的通货膨胀和海关进出口总额之间的关系，以便比较哪一模型的稳健性更好．

1 分位数回归模型

分位数回归模型[1-2]是关于因变量的条件分位数和自变量之间线性关系的估计方法，即由分位数取0 – 1之间的任何值来调节回归平面的位置和转向，让自变量估计不同分位数的因变量．它在一定程度上代表所有数据的信息，特别是特定区域（如极端位置）的数据．

在不同的τ下就能得到不同的分位数函数．随着τ从0取到1即可得到所有z在x上条件分布的一簇曲线；而且随着计算机技术的发展，求回归系数b(τ)的各种算法现在也可以通过统计软件实现．

2 局部线性回归的估计

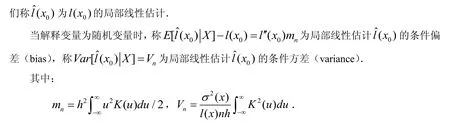
不变窗宽的局部线性估计是局部化的线性回归模型加权的最小二乘估计，在局部用直线来近似曲线，因此，不变窗宽局部线性估计在内点处的收敛速度和边界点处的一样，即不存在边界效应的问题．

下面我们只给出解释变量为随机变量的不变窗宽的估计性质．

3 实证研究

3.1 数据的来源及说明

居民消费价格指数是反映通货膨胀的重要指标．本文用居民消费价格指数来代替通货膨胀指标．记CPI为居民消费价格指数，TIE为海关商品进出口总额（亿美元）．采用2008年01月份到2011年06月份42个月的月度资料，运用分位数回归方法和局部线性回归方法分别对通货膨胀与海关进出口总额的关系进行实证分析．相关的居民消费价格指数资料取自宏观财经-凤凰网（http://app.finance.ifeng.com/data/mac/jmxf.php），要将该数据转换成基期相同（按照国家统计局公布的物价指数以2000年价格为基期）的可比价格数；海关商品进出口额资料来自东方财富网（http://data.eastmoney.com/cjsj/hgjck.html）．居民消费价格指数CPI和海关商品进出口总额TIE的月度数据如表1所示：

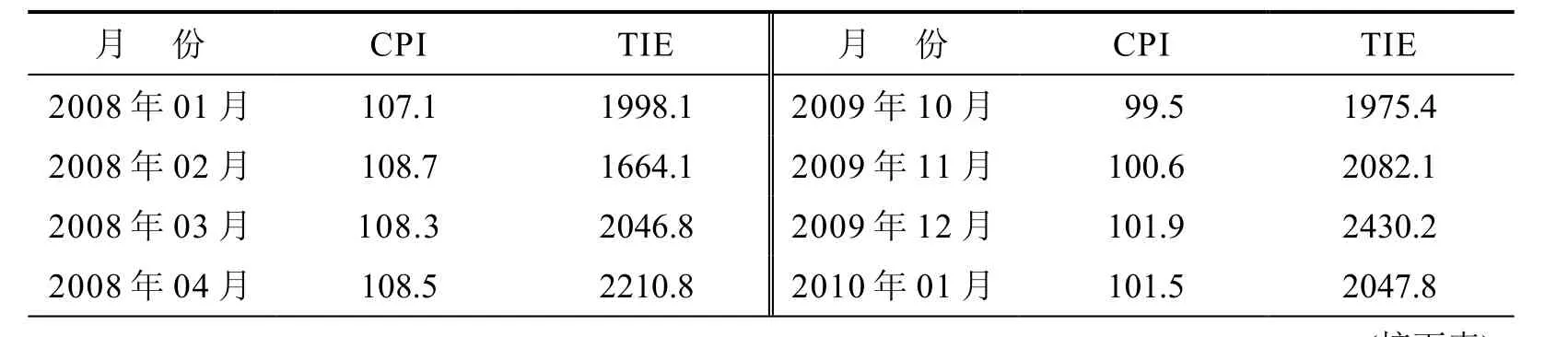
表1 居民消费价格指数CPI和海关商品进出口总额TIE（亿美元）的月度数据

2008年05月 107.7 2213.1 2010年02月 102.7 1814.3 2008年06月 107.1 2215.9 2010年03月 102.4 2314.6 2008年07月 106.3 2480.7 2010年04月 102.8 2381.6 2008年08月 104.9 2408.7 2010年05月 103.1 2439.9 2008年09月 104.6 2434.6 2010年06月 102.9 2547.7 2008年10月 104.0 2214.2 2010年07月 103.3 2623.1 2008年11月 102.4 1898.9 2010年08月 103.5 2585.7 2008年12月 101.2 1833.4 2010年09月 103.6 2731.0 2009年01月 101.0 1417.9 2010年10月 104.4 2448.1 2009年02月 98.4 1249.5 2010年11月 105.1 2837.6 2009年03月 98.8 1620.2 2010年12月 104.6 2952.2 2009年04月 98.5 1707.4 2011年01月 104.9 2950.1 2009年05月 98.6 1641.3 2011年02月 104.9 2007.8 2009年06月 98.3 1825.7 2011年03月 105.4 3042.6 2009年07月 98.2 2002.1 2011年04月 105.3 2999.5 2009年08月 98.8 1917.0 2011年05月 105.5 3012.7 2009年09月 99.2 2189.4 2011年06月 106.4 3016.9

3.2 分位数回归理论建模

考虑我国居民消费价格指数（CPI）与海关进出口总额（TIE）之间的线性关系，采用一元条件分位数回归模型：

下面我们只给出中位数回归的模型及最小二乘回归估计的结果：

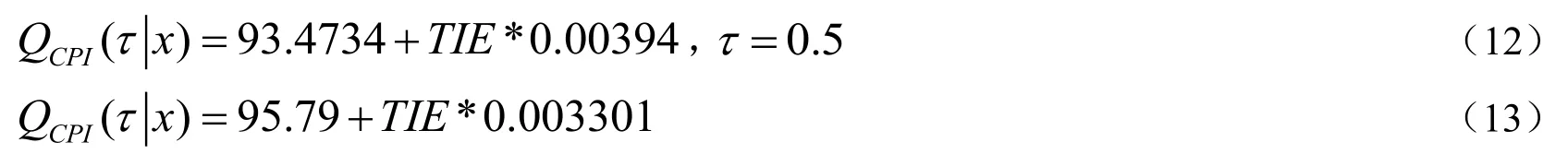
从（12）式、（13）式可以看出OLS回归的均值要高于中位数回归的模型估计，当分位数τ的值分别取0.01，0.05，0.09，0.1，0.2，0.25，0.5，0.75，0.8，0.85，0.90，0.95，0.99时，所得的结果如图1所示①主要考虑在极端值的情况下, 分位数回归估计的效果如何, 所以选择比较偏向左尾和右尾的数据.．

观察图1可得，对于局部线性回归估计未能很好的反映出的奇异值的变化情况，分位数回归在τ取遍0 – 1内的所有值时，尤其是在分位数τ足够小或是逐渐接近于1时，我们可以看到，分位数回归对极端值的估计拟合的更好．对于每一个分位数都可以很好的反映出局部的有针对性的信息，当τ走遍0到1时，就可以将整体数据的全面信息都反映出来了．

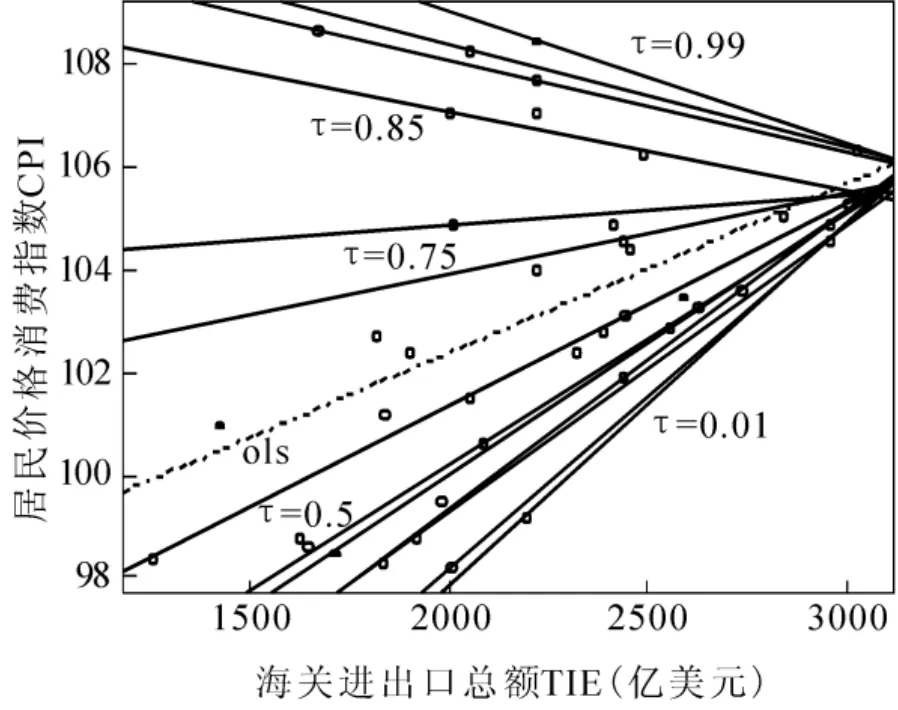
图1 线性分位数回归模型估计的拟合图

当分位数较小时，对于同一个分位数，拟合直线的斜率为正，说明居民消费价格指数（CPI）随海关进出口总额（TIE）的增加而增加；当分位数接近1时，拟合直线的斜率为负，表明随着TIE的增加CPI反而降低了．当斜率为正且越来越小时，国家可根据TIE现状对货币和财政政策进行相应的宏观调控；当斜率为负且越来越小时，TIE对于CPI的影响在逐渐减小，国家也应相应减少针对货币和财政政策的调整．因此，国家可依据统计分析的结果，制定相应的政策．这样建立的模型具有较强的实用性强，并随着计算机技术的迅猛发展，对分位数回归的实现已经有多款软件可以实行，如Matlab，R，SAS，Stata等程序软件和Eviews6.0等操作软件．

3.3 局部线性回归建模

利用所收集的有关通货膨胀的数据（CPI指标来代替）和海关贸易进出口总额（TIE）的数据，建立模型（8）进行非参数的局部线性回归估计（局部线性估计时用统计学软件R[5]中的locfit()函数），得到的结果如图2所示：

从图2可以看出，局部线性回归模型的斜率在一直变化，基本上把居民消费价格指数随商品进出口总额的总体变化趋势描述出来了．从拟合曲线上我们得到开始时当海关进出口总额增加时，曲线斜率为正，而且越来越大，CPI的大多数值就会不断的上升；随后斜率变为负值，CPI的值总体上有下降的趋势，随后有所上升．但是，我们还可以看到在拟合曲线的上方数据和下方数据都没有准确的拟合出来，这样势必会造成一部分信息的丢失，没有完整的把奇异值的代表信息反映出来，建立的模型在稳健性方面就会有些质疑了．

图2 局部线性回归的估计拟合图

4 结 论

在介绍分位数回归模型和局部线性回归模型理论的基础上，并就这两种模型对我国的海关进出口总额在通货膨胀中的表现做了对比分析，由图形得到，分位数回归模型具有更加稳定的特性．在研究通货膨胀和海关进出口总额之间关系时，使用分位数回归模型更加有效．

[1] 李育安. 分位数回归及应用简介[J]. 统计与信息论坛, 2006, 21(3): 35-38.

[2] Wang X W. The Two Comparative Study of Methods Based on the Financial Risk Empirical Analysis [C] // 吴仰儒,李延喜. 第三届(2011)金融风险与公司金融国际研讨会论文集. 大连: 大连理工大学出版社, 2011: 796-799.

[3] 叶阿忠. 非参数计量经济学[M]. 天津: 南开大学出版社, 2003: 63-69.

[4] 王星. 非参数统计[M]. 北京: 清华大学出版社, 2009: 203-225.

[5] 汤银才. R语言与统计分析[M]. 北京: 高等教育出版社, 2008: 7-68.

Comparison of Robustness in Estimation of Quantile Regression and Local Linear Regression

WANG Xiuwen1, WANG Jingxu2
(1. School of Mathematics and Information Science, Wenzhou University, Wenzhou, China 325035;
2. School of Economics and Management, Huazhong Agricultural University, Wuhan, China 430000)

Based on the introduction of theory of quantile regression estimation method and of local linear regression estimation method, separate models were established to analyze relations between China’s inflation and volume of customs import and export from 2008 to 2011. Results showed that: while quantile regression estimation method is more robust; in study of relations between inflation and the volume of customs import and export, quantile regression model is more effective.

Quantile Regression; Local Linear Regression; Inflation; Volume of Customs Import and Export; Robustness

O212

A

1674-3563(2012)06-0007-06

10.3875/j.issn.1674-3563.2012.06.002 本文的PDF文件可以从xuebao.wzu.edu.cn获得

(编辑：封毅)

2011-12-21

王秀文(1985- )，女，山东聊城人，硕士研究生，研究方向：应用统计