带有粘性阻尼摆的自参数振动系统混沌研究

张文娟，俞建宁，安新磊，杨留猛

(兰州交通大学数理与软件工程学院，甘肃兰州 730070)

带有粘性阻尼摆的自参数振动系统混沌研究

张文娟，俞建宁，安新磊，杨留猛

(兰州交通大学数理与软件工程学院，甘肃兰州 730070)

对一类带有粘性阻尼摆的自参数振动系统的复杂动力学行为进行研究．根据系统运动的拉格朗日方程和牛顿第二定律，建立了系统的动力学方程，借助Poincaré截面和分岔图研究了系统的混沌行为，通过数值仿真得到其相图、Poincaré映射图、分岔图和Lyapunov指数谱，进而证明了该模型是混沌数学模型；对该系统弹簧振子刚度的增加，可导致该系统产生新的混沌区域．

自参数振动系统；混沌；Poincaré映射图；分岔图；Lyapunov指数谱

非线性因素是任何振动系统都存在的，它们来自系统物理的、结构的、耗散的、运动的以及这些非线性的组合等方面．与参数化的系统不同，自参数系统涉及至少两种模式内部耦合引起的振动．从数学的角度来看，激励来自运动方程[1]中呈现的非线性耦合项．自参数振动[2]一般由两部分组成，第一部分是主振动系统，它在外激励、参变激励或者是自激励作用下振动，第二部分为次系统（也称为被激系统），次系统不直接受到激励的作用，一般不随着主系统振动，主系统实际上就充当了次系统的参变激励．自参数共振使得次系统吸收主系统的振动，从而抑制主系统的振动．自参数振动系统因为其丰富的动力学现象以及广泛的工程背景，受到许多学者的关注．例如，Hatwal等[3]研究了自参数振动系统受到谐波激励时产生的周期和混沌等运动；Cuvalci和Ertas[4]对一个以摆为辅助系统的悬臂梁自参数振动系统进行了研究．本文对一类带有粘性阻尼摆的自参数振动系统进行了研究，探讨了该系统的复杂动力学行为[5-7]，包括相轨迹图、Poincaré映射图、分岔图和Lyapunov指数谱等，证实了该混沌系统存在，通过改变该系统弹簧振子刚度，可使系统混沌区域发生变化．

1 自参数振动系统模型

带有粘性阻尼摆的自参数振动系统如图1所示，它由两个主要的子系统构成,分别为：

由于外激励作用，非线性振子受迫于一线性弹簧．假定弹簧振子为非线性Duffing型振子，即

以垂直方向的位移x和单摆的角度位移φ为广义坐标，运用拉格朗日第二类方程和牛顿第二定律，建立系统的运动微分方程：

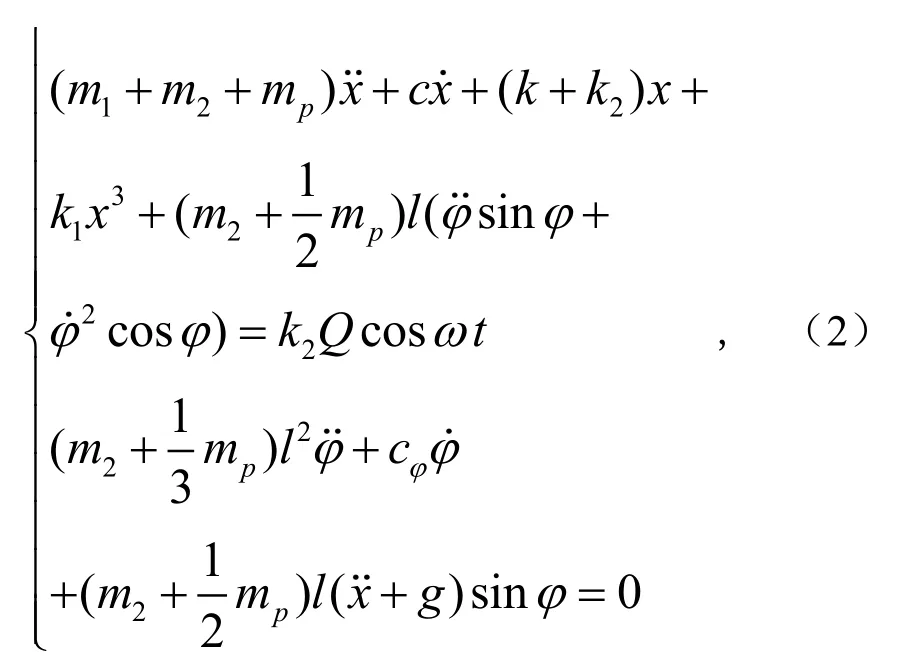
式中，cφ是单摆的粘性阻尼系数，c是振子的阻尼系数，l是单摆的长度．

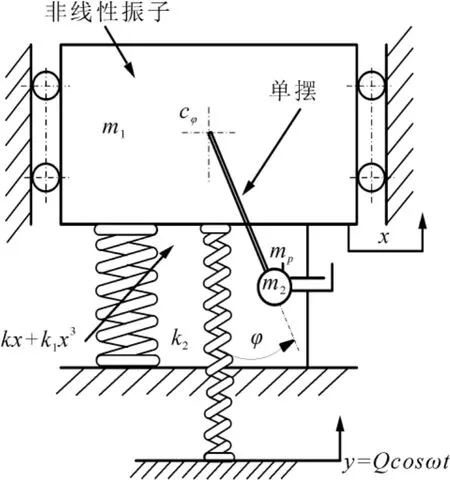
图1 系统力学模型

为了便于分析，引入下列无量纲量：

于是，系统无量纲化的运动微分方程为：

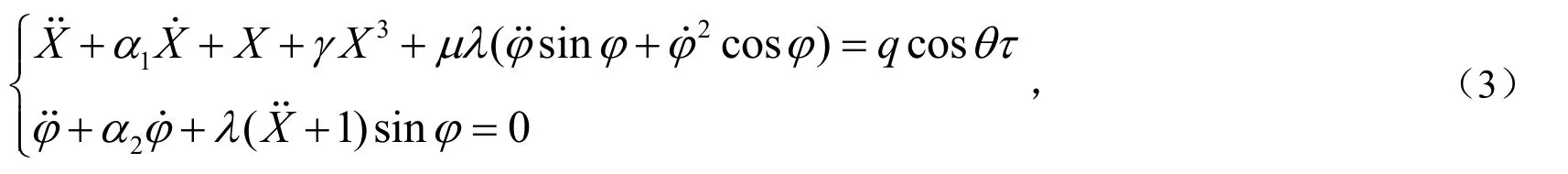
这里，方程（3）中的自参数激励是由耦合项即单摆角度位移φ的二阶导数和一阶导数平方所引起的．

2 系统混沌现象分析

2.1 系统的混沌数学模型

将上述方程（3）转化为一阶微分方程组的形式，即

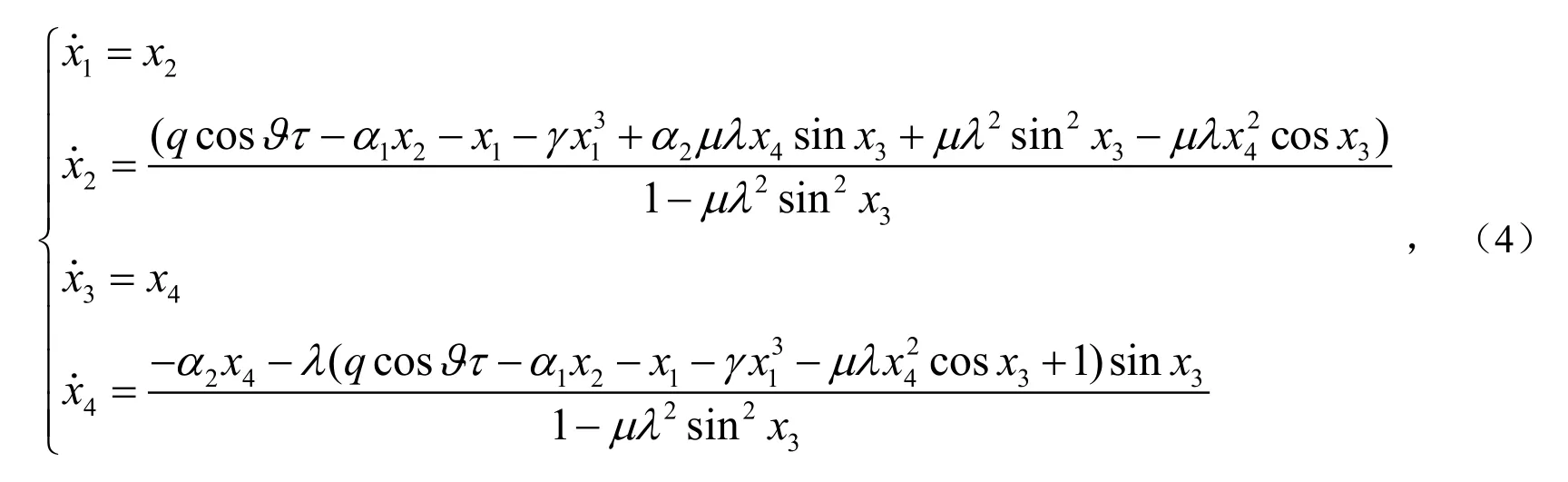
图2 系统的混沌吸引子相图

2.2 分岔图和Lyapunov指数谱

由图3可知，当激励频率参数θ在0.6到0.62范围取值时，出现混沌现象，这时的运动仅是由摆动构成的不规则吸引子；当激励频率参数θ在0.63 – 0.72和0.98 – 1.19时，混沌运动是由单摆的旋转和摆动共同构成的；当激励频率参数θ位于0.73到0.97之间时，单摆执行完全的旋转．

由Lyapunov指数谱、分岔图可直观反映出非线性动力学系统随参数变化的动态特性，当有一个Lyapunov指数大于0时，系统处于混沌状态．系统的Lyapunov指数谱如图4所示．由图4可知，随着参数θ的变化，在区域0.6 – 0.72和0.98 – 1.19内系统的最大Lyapunov指数从小于0变化到大于0，亦即系统在这两个区域是混沌运动状态，这与系统的分岔图（图3）完全吻合．

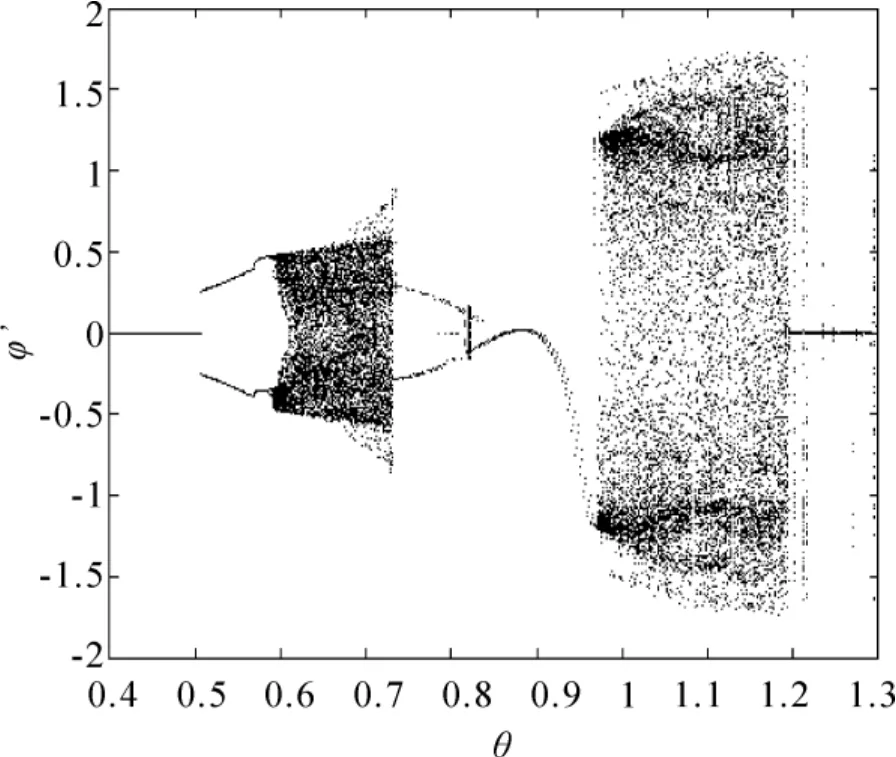
图3 分岔图

图4 Lyapunov指数谱

图5 系统对于不同γ值的分岔图

2.3 系统的Poincaré映射图

Poincaré映射是一种经典的分析动力系统的技术，可以通过观察Poincaré截面上截点的情况来判断是否发生混沌．当Poincaré截面上是一些成片的具有分形结构的密集点时，运动是混沌的．通过Poincaré映射图还可以观察系统的动力学行为，根据Poincaré截面上点的情况，可以判断系统的运动情况．该系统属于非自治系统，数值计算中，每隔2π周期取相轨线上的点，可得到系统的Poincaré映射图，如图6所示．

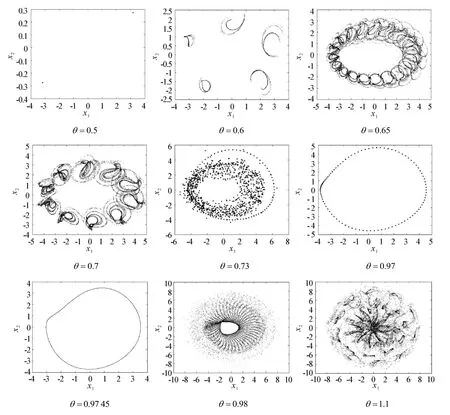
图6 系统的Poincaré映射图

3 结 语

本文建立了一个带有粘性阻尼摆的自参数振动模型，分析了其复杂动力学特征，包括分岔图、Lyapunov指数谱及Poincaré映射图等，证实了该混沌系统的存在性．数值仿真结果表明，增加弹簧振子刚度，可导致该系统产生一种新的混沌区域，因此采用非线性的弹簧振子刚度似乎是一种提高动力吸收现象的理想方法.

参考文献

[1] Warminski J, Kecik K. Instabilities in the main parametric resonance area of a mechanical system with a pendulum [J]. Journal of Sound and Vibration, 2009, 322(3): 612-628.

[2] 赵艳影, 徐鉴. 利用时滞反馈控制自参数振动系统的振动[J]. 力学学报, 2011, 43(5): 895-904.

[3] Hatwal H, Mallik A K, Ghosh A. Nonlinear vibration of a harmonically excited autoparametric system [J]. Journal of Sound and Vibration, 1982, 81: 153-164.

[4] Cuvalci O, Ertas A. Pendulum as vibration absorber for flexible structures: experiments and theory [J]. Journal of Vibrations and Acoustics, 1996, 118: 558-566.

[5] 刘秉政, 彭建华. 非线性动力学[M]. 北京: 高等教育出版社, 2004: 120-150.

[6] 刘延柱, 陈立群. 非线性振动[M]. 北京: 高等教育出版社, 2001: 268-269.

[7] 张阿舟, 诸德超, 姚起航. 实用振动工程: 振动控制与设计[M]. 北京: 航空工业出版社, 1997: 136-149.

Chaos of the Autoparametric Vibration System with a Viscous Damping Pendulum

ZHANG Wenjuan, YU Jianning, AN Xinlei, YANG Liumeng
(School of Mathematics and Software Engineering, Lanzhou Jiaotong University, Lanzhou, China 730070)

According to Lagrange equation of the dynamic motion and Newton's second law, the paper makes a study on the complex dynamic behavior of a kind of autoparametric vibration system with a viscous damping pendulum and thus establishes the kinetic equation of the system. With the help of the Poincaré sections and the bifurcation diagram, the paper has studied the chaotic behavior of the system, and then obtained its phase diagram, Poincaré map, bifurcation diagram and Lyapunov exponent spectrum by numerical simulation, and thus proved that the model is a chaotic mathematical one. And the increase of the spring oscillator stiffness of the system will cause the system to produce a new chaotic region.

Autoparametric Vibration System; Chaos; Poincaré Map; Bifurcation Diagram; Lyapunov Exponent Spectrum

O322

A

1674-3563(2012)06-0019-06

10.3875/j.issn.1674-3563.2012.06.004 本文的PDF文件可以从xuebao.wzu.edu.cn获得

(编辑：王一芳)

2012-03-16

甘肃省自然科学基金(1010RJZA066；1010RJZA067)

张文娟(1987- )，女，甘肃兰州人，硕士研究生，研究方向：应用数学