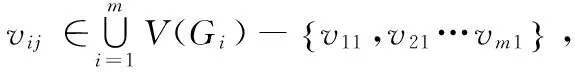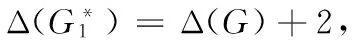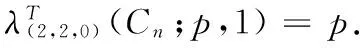某些特殊图类的非正常(p,1)-全标号

2012-05-25孙丽娇孙磊

枣庄学院学报 2012年2期

孙丽娇，孙磊

(山东师范大学数学科学学院，山东济南 250014)

1 引言

在频率分配问题中，假如给定一些基站，为避免干扰，需给每个基站分配一个整数的频率波段，要求非常近的基站间必须是至少差2个频道的，稍近的一些基站分配不同的频道.受到这个问题的启发，Griggs和Yeh[1]引入了L(2,1)-标号，它的自然推广就是图G的L(p,1)-标号.在此问题中，若某些中转站不受控制或是已坏掉，则反映到标号问题中，即可允许某些顶点标号不受限制.Whittlesey等人在文献[2]中研究了G的剖分图的L(2,1)-标号，G的剖分图S1(G)是由图G在每条边上插入一个点所得到的图.S1(G)的L(p,1)-标号对应于G的L(p,1)-全标号.自然地，有如下定义：

定义1.1[3]设p是一个非负整数，图G的一个k-(p,1)-全标号是一个映射f:V(G)∪E(G)→{0,1,…k}，使得：

(1)G的任意两个相邻的顶点u和v，有|f(u)-f(v)|≥1；

(2)G的任意两条相邻的边e和e′，有|f(e)-f(e′)|≥1；

(3)G的任意两个关联的点u和边e，有|f(u)-f(e)|≥p.

定义1.2 设p,r,s,t是非负整数，图G的一个非正常(r,s,t)-(p,1)-全标号是一个映射f:V(G)∪E(G)→{0,1,2,…k}，使得：

(1) G的任意两个相邻的顶点u和v，对∀u∈V(G),其邻接顶点中除至多r个点外，有|f(u)-f(v)|≥1；

(2) G的任意两条相邻的边e和e′，对每一e∈E(G),其邻接边中除至多s条边外，有|f(e)-f(e′)|≥1；

(3) G的任意两个相邻的边e和顶点v，对每一顶点v∈V(G)，其关联边中除至多t条边外，均有|f(e)-f(v)|≥p；对每一条边e∈E(G)，其关联点中除至多(t≤2)个顶点外，均有|f(e)-f(v)|≥p.

对任两相邻顶点u和v，若f(u)=f(v)，则称u和v为一对坏点.

对任两条相邻边e和e′，若f(e)=f(e′)，则称e和e′为一对坏边.

定义1.3[4]对两个图G和H，笛卡尔乘积图G□H定义如下：

V(G□H)=V(G)×V(H),

E(G□H)={(u,v)(u′,v′)|v=v′且uu′∈E(G)或u=u′且vv′∈E(H)}.

定义1.4[5]G为简单图，V(G)={v1,v2,…,vn}，把m个G的顶点vj0∈G(j0∈{1,2,…n})连成圈，所得到的新图，记为Cm·G(vj0)，简记为G*.即Gi(i=1,2,…m)为G的m个复制图，新图G*的点集和边集为：

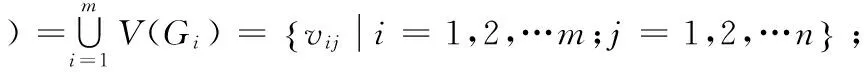
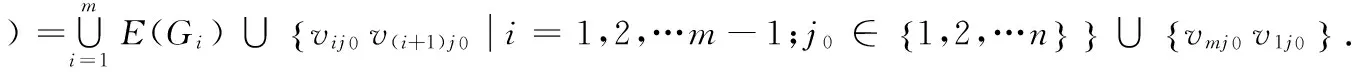
定义1.5[5]Cn是一个圈，设V(Cn)={v1,v2,…,vn}，V(Cn)的一个复制记为{u1,u2,…,un}.定义新图Sn的顶点集和边集如下：

V(Sn)={v1,v2,…,vn,u1,u2,…,un}；

E(Sn)=E(Cn)∪ {uivi,i=1,2,…n}∪ {unv1,u1v2,…un-1vn}.

本文未加说明的定义及标记参见参考文献[6].

2 主要结果及其证明

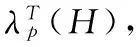
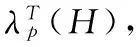
首先给Pm□H中的顶点标号：当i∈{1,2,…m+1}时，对∀(ui,vj)∈V(Pm□H)，令f*(ui,vj)=f(vj)+1(j=1,2,…n).

其次对Pm□H中的边标号：先给边(ui,vk)(ui,vl)标号，令：

f*((ui,vk)(ui,vl))=f(vkvl)+1(i=1,2,…m+1;k,l=1,2,…n且k≠l)；

其次对边(uk,vj)(ul,vj)标号(k,l=1,2,…m+1且k≠l,j=1,2,…n)，分情况讨论：

(1)若在H中存在vj邻边e，使f(vj)

(2)若在H中，vj的邻边标号均比vj的标号小，则令f*((uk,vj)(ul,vj))=0.

易证f*是Pm□H的一个非正常(2,2,0)-(p,1)-全标号.

证明：v1为G中一最大度点，由引理知，f(v1)=0或f(v1)=Δ(G)+p-1，不失一般性，可设v1在原图G中的标号为Δ(G)+p-1.

对∀vi1，令f*(vi1)=Δ(G)+p(i=1,2,…m)；

对∀vi1vi+1,1(i=1,2,…m-1)，令f*(vi1vi+1,1)=Δ(G)且f*(vm1v1,1)=Δ(G)；

证明：可设V(Cn)={v1,v2,…,vn}，f为Cn的一个非正常(2,2,0)-(p,1)-全标号，则标号如下：首先对顶点标号：当i∈{1,2,…n}，令f(vi)=0.其次对边标号，当i∈{1,2,…n-1}，令f(vivi+1)=p，f(vnv1)=p.至此完成Cn的一个非正常(2,2,0)-(p,1)-全标号.