跷跷板控制系统设计
2012-05-25李婷
李婷
(枣庄学院 数学与统计学院,山东 枣庄 277160)
1 引言
自20世纪50年代末现代控制理论诞生以来,控制理论得到了飞速的发展,并在20世纪60年代的航天领域中得到成功的应用[1].现代控制理论的许多结果都是基于对象的一个数学模型,根据系统的性能要求,通过对被控对象的数学模型进行分析来设计系统的控制律,进而将所得到的控制律应用于被控对象来保证闭环系统具有所期望的性能[2].
系统建模即对系统建立模型,在系统控制理论中具有基本的重要性.跷跷板系统的结构主要由防止在横梁上的小球和驱动转盘组成.随着转盘的转动,横梁的倾斜角度也随之变化.小球在重力的作用下将沿着横梁自由滚动[3].本文针对跷跷板系统控制系统,忽略横梁与小球之间的滚动摩擦,建立模型,其目的在于深入和定量地揭示系统行为的规律性或因果关系性,其建模的实质是对系统的动态过程即各个变量和参量间的关系按照研究需要的角度进行描述. 设计状态反馈控制器的最简单方法是采用极点配置[4].其基本思想是首先确定闭环系统N个根极点的期望位置,然后设计适当的反馈增益,从而将系统的极点调整到期望的位置.如果系统是完全可控的,则这一过程完全可以表示成包含N个未知参数的N个方程组的求解。所需要设计的反馈控制增益就是该方程组的解.
在建立模型的基础上,采用极点配置设计控制器,使得小球可以停留在横梁的任意位置.并利用状态能控性定理、李雅普诺夫稳定性定理、matlab程序动态仿真模拟,验证是否使系统达到稳定的状态.从而揭示跷跷板系统控制系统的状态的规律性,最后给出两组不同的数据对系统性能进行了简单的分析.
2 准备知识
线性系统的状态方程和输出方程可表示为如下的一般形式:

(2.1)
特别地,若式(2.1)中系统矩阵A(t),B(t),C(t),D(t)是与时间变量无关的定常矩阵,这时被控过程是一个线性定常系统,其状态空间描述为

(2.2)
其中:A,B,C,D分别为n×n,n×r,m×n,m×r维常数矩阵.
AHP+PA=-Q
这里H表示Hermite矩阵或实对称矩阵.此时,Lyapunov函数为


线性系统稳定性概念与Lyapunov意义下的稳定性概念
3 问题的提出及系统建模
3.1 问题的提出与条件假设
跷跷板系统的结构如图3.1所示,它主要由防止在横梁上的小球和驱动转盘组成.随着转盘的转动,横梁的倾斜角度也随之变化.小球在重力的作用下将沿着横梁自由滚动.控制的目的是使小球可以停留在横梁的任意位置上.(忽略横梁与小球之间的滚动摩擦)

图3.1 跷跷板系统的结构示意图
本文做如下条件假设
M--------------------------小球的质量(0.11千克)
R--------------------------小球的半径(0.015米)
d--------------------------杠杆臂的偏移(0.03米)
g--------------------------重力加速度(9.8m/s2)
L--------------------------横梁的长度(1.0m)
J--------------------------小球的瞬时惯量(9.99e—6kg.m2)
R--------------------------小球的位置坐标
α-------------------------横梁的倾斜角度
θ--------------------------侍服齿轮的角度
3.2 系统分析及建模
针对小球的运动可以建立它的Lagrangian方程

(3.1)
将上式在α=0处线形化,得到小球的线形化运动方程
(3.2)
横梁的倾斜角度与侍服齿轮的角度具有如下的近似线形关系
将上式代入式 (3.2) 中得到
(3.4)
1)传递函数
假设系统的初始条件为零,将上式进行Laplace变换,得到下面对的方程
(3.5)
从而得到系统的传递函数描述
(3.6)
2)状态空间描述
该系统的线形化模型也可以使用标准状态空间模型进行描述.将小球的位置坐标(r)和小球运动的速度作为系统的状态变量.于是,系统地状态方程可以写成在这个模型中,将通过控制α的二阶导数而不是侍服齿轮的角度来达到控制小球位置的目的。从而得到如下的系统方程:
(3.7.1)
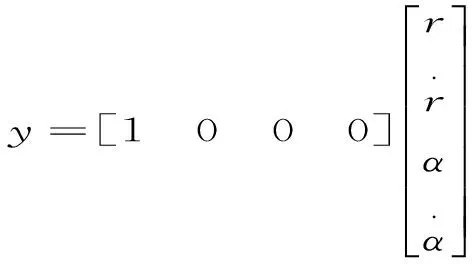
(3.7.2)
上面这个模型中,没有用到侍服齿轮和杠杆臂,而是通过安装在横梁中心的电机对横梁施加适当的力矩来控制小球的位置.一般也称该模型为力矩控制模型.
4 控制器设计及稳定性分析
下面我们为系统设计全状态反馈控制器.控制系统示意图如下所示.

图4.1 全状态反馈控制系统示意图
4.1 系统可控性判别
若将式(3.7)描述成状态空间(2.2)的形式,根据假设3.1.2的相关数据,可得

D=[0] .
4.2 设计全状态反馈控制器
全状态反馈控制系统的闭环特征多项式为(sI-(A-BK)),在本文中,A和B*K都是4*4矩阵,因此系统因该具有4个极点.设计全状态反馈控制器的目标就是将这些极点移动到期望的位置.根据系统的设计要求,计算出期望的主导极点位置位于-2+2i和-2-2i处,其它的极点应该远离主导极点.所以有
p1=-2+2i;p2=-2-2i;
情形1.初始假定:p3=-20;p4=-80
以下是跷跷板系统的可控性分析:
首先代入给定的p1,p2,p3,p4的值可得:随后通过MATLAB可以计算出控制器的增益矩阵.得到的计算结果为

将计算得到的增益矩阵K带入状态方程,最终的闭环系统状态方程为

Y=Cx
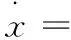

ans =1.0e+003 *
进一步地结合多源流分析框架梳理媒体影响计划生育政策变迁的逻辑机制,可以归结出媒介融合背景下媒体影响政策变迁的基本逻辑:一是在问题流中,通过构建明晰指标、推动焦点事件、持续问题反馈提升触发机制效果;二是在政策流中,通过呈现民间话语、强化专家声音、构建良性对话推动政策共同体之间的虚拟接触博弈;三是在政治流中,通过汇聚网络民意、打造意见领袖激活国民舆论热情。同时,传统媒体与新媒体在影响路径上有所差异(见图8)。
0 0.0010 0 0
0 0 0.007 0 0
0 0 0 0.0010
-1.8286 -1.0286 -2.0080 -0.1040
当初始状态分别设置为x0=[0.1 0 -0.1 1]的响应,如下列图所示

图4.1 闭环系统初始状态响应
接下来可以仿真闭环系统在0.25m输入信号下的阶跃响应,将计算得到的增益矩阵K带入状态方程,最终的闭环系统状态方程为

v=0.25m
运行matlab程序,得到的系统响应曲线如图所示

图4.2 闭环系统阶跃响应图
因此反馈闭环系统具有一定的抗干扰能力.
情形2.将主导极点改为p1=-1+1i;p2=-1-1i;
初始假定:其他两个极点改为p3=-10;p4=-75,以便于进行结果比较.
以下是跷跷板系统的可控性分析:
代入给定的p1,p2,p3,p4的值可得:
随后通过MATLAB的place命令可以计算出控制器的增益矩阵.以下是相应的程序代码:
p1=-1+1i;p2=-1-1i;p3=-10;p4=-75;K=place(A,B,[p1,p2,p3,p4])
得到的计算结果为
K = 214.2857238.5714922.0000 87.0000
将计算得到的增益矩阵K带入状态方程,最终的闭环系统状态方程为
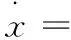

初始状态分别设置为x0=[0.1 0 -0.1 1]的响应,编制和执行和情形1类似的程序可得闭环系统初始状态响应图4.2如下

图4.3 闭环系统初始状态响应图
同样,我们接下来可以仿真闭环系统在0.25m输入信号下的阶跃响应,将计算得到的增益矩阵K带入状态方程,最终的闭环系统状态方程为

得到的系统响应曲线如图所示

图4.4 闭环系统阶跃响应图
对两种情形的运行结果图形进行比较可见随着主导极点的聚拢,图形波动幅度有所减小,但二者最终都已达到渐进稳定.
5 结论
本文考虑了一类工程应用中的跷跷板模型问题,使用MATLAB对其进行建模与仿真[5],并采用了极点配置理论设计控制器.结论表明:随着主导极点和其他极点(控制)的改变,线性系统有一个波动的过程,但其稳定状态不会发生较大的变化,而且可以仿真闭环系统在一定的输入信号下的阶跃响应来验证此系统的稳定性.
参考文献
[1]俞立 编著.鲁棒控制-线性矩阵不等式处理方法[M].北京:清华大学出版社,2002.
[2] 俞立 编著. 现代控制理论[M]. 北京:清华大学出版社, 2007.
[3] 赵文峰等,编著. 控制系统设计与仿真[M].陕西:西安电子科技大学出版社, 2002.
[4] 郑大钟 编著.线性系统理论[M].北京:清华大学出版社,2005.
[5] 薛定宇,陈阳泉编著. 基于MATLAB/Simulink的系统仿真技术与应用[M].北京:清华大学出版社, 2003.
