p（x）-Laplace方程解的存在性

刘越里，陈庆娥

（天水师范学院数学与统计学院，甘肃 天水 741001）

p（x）-Laplace方程解的存在性

刘越里，陈庆娥

（天水师范学院数学与统计学院，甘肃 天水 741001）

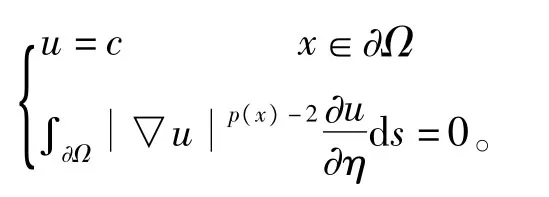
无流边界；p（x）-Laplace方程；最小作用原理

1 引言与性质

近年来，具有变指数问题的研究目前是一个很热的课题，在非线性弹性力学和电子流变流体力学中有着重要的应用［1］。在具p（x）增长性问题的研究中，p（x）-Laplacian方程是其中比较重要的领域。关于p（x）-Laplacian方程的Dirichlet边值问题，Neumann边值问题已有很多结果［2，3］。得到这些结果的主要方法是变分法，上下解方法。本文主要考虑了具有无流边界p（x）-Laplace方程解的存在性，其中无流边界为

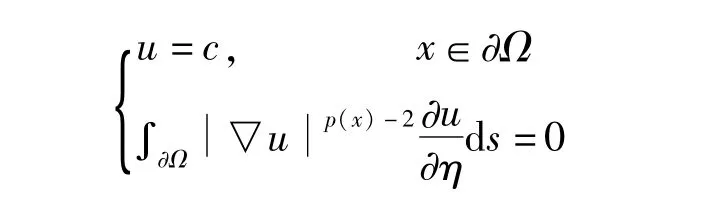
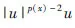
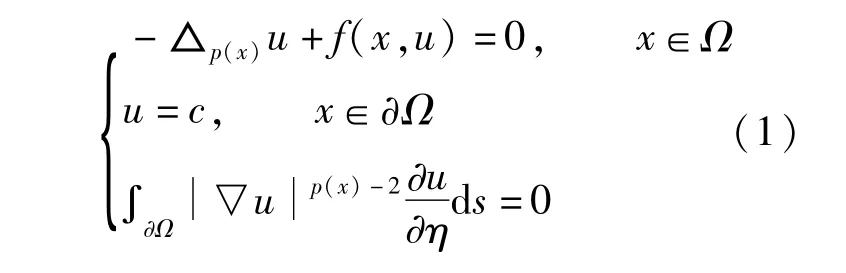
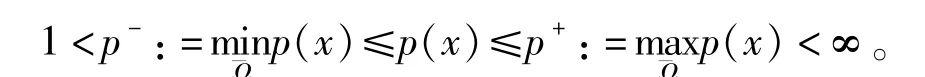
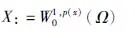
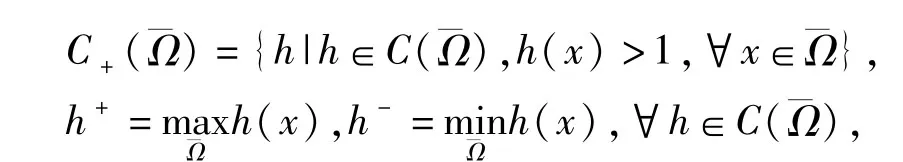
Lp（x）（Ω）：=｛u｜u是Ω上的可测实值函数且∫Ω｜u（x）｜p（x）dx＜∞｝，

Lp（x）（Ω）上的范数为

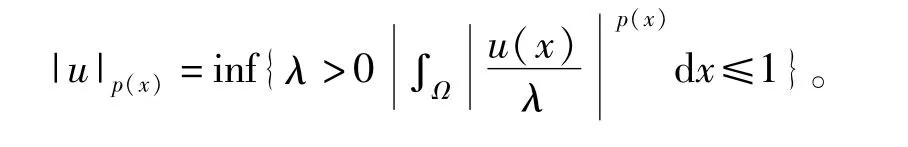
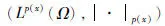
是Banach空间，叫做变指数Lebesgue空间。

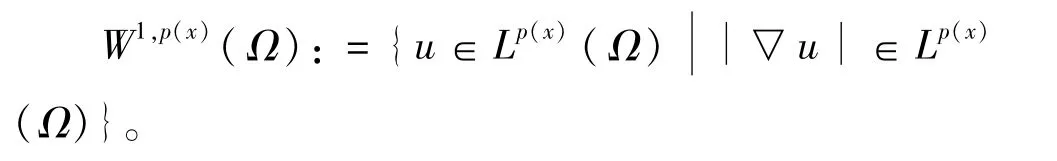
其对应的范数是

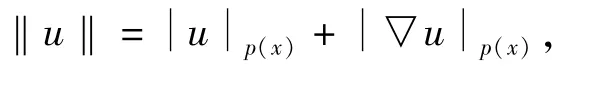
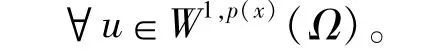
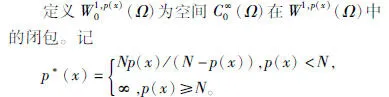
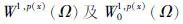
2 最小作用原理与主要结果

下面总假设f满足下述基本假设：

基本假设：假设f满足Caratheodory条件，且

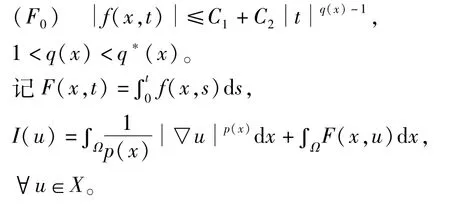
本文主要结果由下面基本定理得到。

最小作用原理［7］：设（F0）满足，若I有一个有界的极小化序列，则I有最小值点。

定理2.1设F（x，t）关于t是T-周期的，即∃T＞0使得

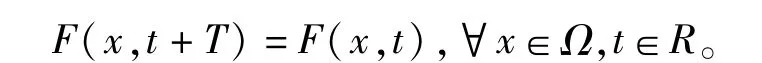
则Ｉ有最小值点。

证明：因为F（x，t）有界，泛函I有下界c＞-∞。下证I有有界的极小化序列。设｛un｝是I的极小化序列，易证▽un%Lp（x）（Ω）有界。

对∀u∈X，有I（u）=I（u+kT），其中k为任意整数。对每个un，可找到某个k（n），使得u¯n+k（n）T≤T。令Vn=un+k（n）T，那么｛Vn｝也是I的极小化序列，¯Vn有界，则｛Vn｝是有界的。所以I有最小值点。即方程（1）有一弱解。

利用类似的方法可得到下面方程解的存在性

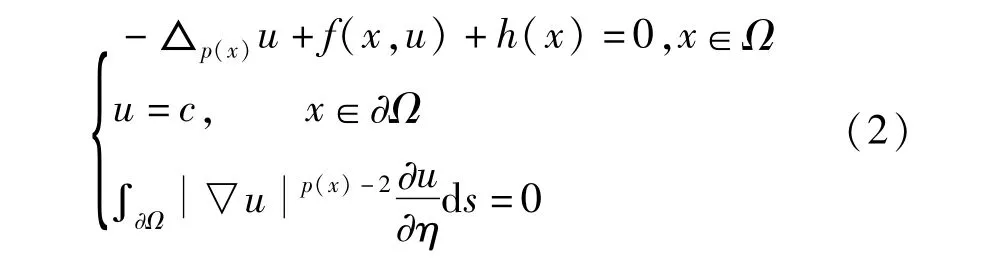
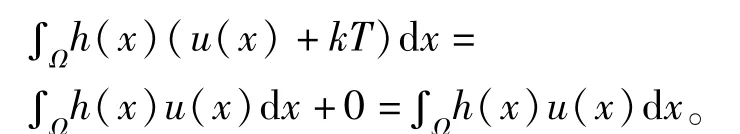
因此有I（u）=I（u+kT）。设｛un｝是I的一个极小化序列，则适当选取kn，令Vn=un+knT，可使得¯Vn有界，而｛Vn｝也是I的极小化序列。这时

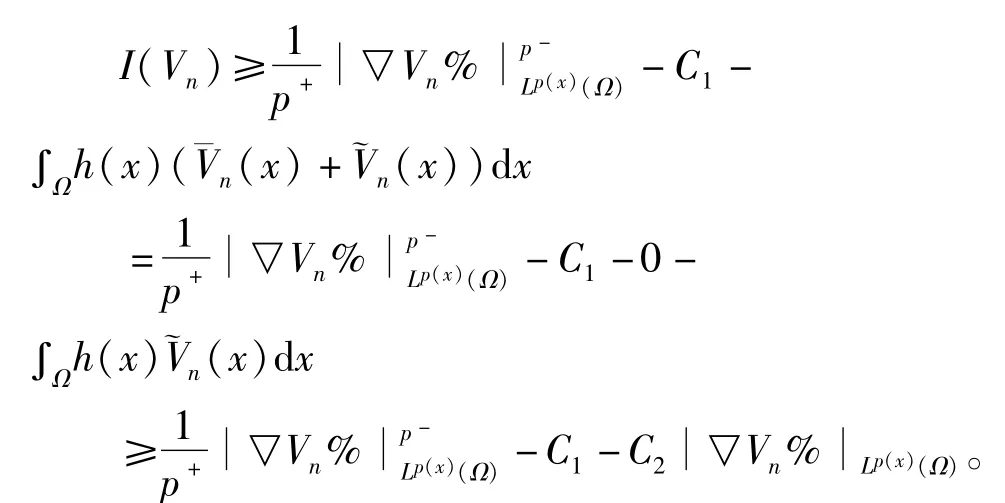
［1］M.Ruzicka，Eleectoroheological fluids.modeling and mathematical theory［M］.Springer Verlag，Berlin，2000.

［2］X.L.Fan.Solutions for p（x）-Laplacian Dirichlet problem with singular coefficients［J］.JMAA.2005，312（3）：464-477.

［3］M.Mihailescu.Existence and multiplicity of solutions for a Neumann problem involving p（x）-Laplacian Laplacian operator［J］.NA.2007，67（5）：1419-1425.

［4］X.L.Fan，D.zhao.On the space Lp（x）and Wm，p（x）（Ω）［J］.JMAA，2001，63（2）：424-446.

［5］X.L.Fan，J.S.Shen，D.zhao.Sobolev embedding theorems for Spaces Wk，p（x）（Ω）［J］.JMAA，2001，62（2）：749-760.

［6］刘越里，陈庆娥，田玉柱.具有无流边界条件的Laplacian算子的特征值［J］.天水师范学院学报，2010，30（2）：38 -40.

［7］张恭庆.临界点原理及其应用［M］.上海：上海科学技术出版社，1986.

［责任编辑 贺小林］

Existence of Solution for p（x）-Laplace Equation

LIU Yue-li，CHEN Qing-e
（School of Mathematics and Statistics，Tianshui Normal College，Tianshui 741001，China）

When a term of｜u｜p（x）-2u is involved in p（x）-Laplace equation，it is easy to get the existence of solution and multiplicity of this equation using mountain pass theorem and fountain theorem.Otherwise，We apply the principle least action to obtain the existence of solution of p（x）-Laplace equation with no flux boundary.

no flux boundary；p（x）-Laplace equation；the principle least action

O175.29

A

1004-602X（2012）03-0037-03

10.3969／J.ISSN.1004-602X.2012.03.037

20120421

甘肃省自然科学基金资助项目（096RJZE106）

刘越里（1981—），女，甘肃天水人，天水师范学院讲师。