正、负顾客依状态到达的M/M/m/(k-m)优先权排队系统

王 玉， 吕胜利， 张 雷

(燕山大学 理学院 河北 秦皇岛 066004)

0 引言

Gelenbe 在20世纪90年代初首次将负顾客引入排队网络[1-2]，排队论的研究领域得到了进一步的扩展.优先权排队也是实际排队系统中常见的现象，在通信网络、电子对抗系统、计算机中断系统、医疗救治系统中，优先权排队有着广泛的应用[3-4].随后，出现了把多服务台和带有优先权同时考虑的排队系统[5-6]，也有学者对带有优先权和有限空间的排队进行了尝试性探究[7].但是对在2类顾客中分别考虑强占优先权和负顾客的情况研究较少，在有限等待空间的基础上同时考虑到多服务台和依状态到达的研究则更少. 本文正是基于对通信网络系统中语音信号的传递和处理较数据信号具有优先权、信号传输速率和服务率的变化、外来信号和病毒对数据信号的干扰的实际应用背景而建立的排队模型，为系统优化提供了理论依据.

1 模型描述

系统中有m个服务台，一个等待区域，等待空间为(k-m)(k≫m).有2类顾客且均无等待时间限制.第1类顾客较第2类顾客具有强占优先权，只有当第1类顾客数少于服务台数时第2类顾客才能接受服务，即使第2类顾客正在接受服务，这时若有第1类顾客到达，则马上停止对第2类顾客的服务而对刚到达的第1类顾客服务，被抢占的此第2类顾客回到原来等待轨道的队首重新等待.服务规则是先到先服务.在服务台全忙且正在接受服务的全是第1类顾客的时候，若等待空间未满则新到来的第1类顾客自动排到轨道的队首等待接受服务.系统中的第2类顾客会受到负顾客的干扰，负顾客的到达只对第2类顾客实行RCE抵消策略，即使第2类顾客正在接受服务，负顾客不接受服务.

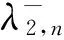
其中n表示系统中已有的顾客数，当n=0时，第2类正顾客以参数λ2的泊松流到达，由此可知，随着系统中顾客数目的增多，第2类正顾客的到达率逐渐降低而负顾客的到达率逐渐升高.

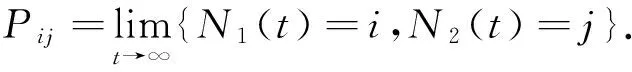
2 模型分析

2.1 稳态下的平衡方程

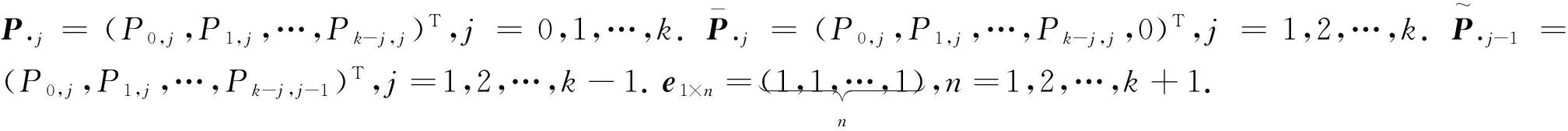
1) 由稳态分析可得下列状态转移平衡方程：

j=0时，

mμ1Pk，0=λ1Pk-1,0.

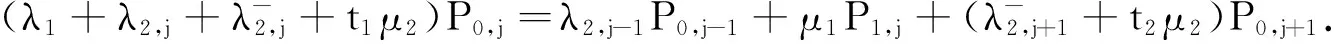
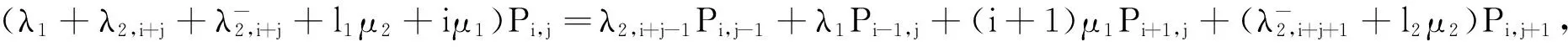
j=k-m+1,…,k-1时，

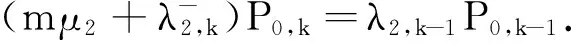
2) 把以上的平衡方程化为矩阵形式

当j=0时，

(1)

其中,f0=λ1+λ2,0，ft=λ1+λ2,t+tμ1(t=1,2,…,m)，ft=λ1+λ2,t+mμ1(t=m+1,…,k-1)，fk=mμ1，gt=-tμ1(t=1,2,…,m)，gt=-mμ1(t=m+1,…,k).

当j=1,2,…,k-1时，

(2)

当j=1,2,…,k-m时，

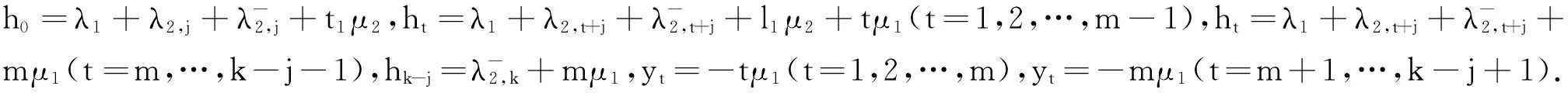
当j=k-m+1,…,k-1时，

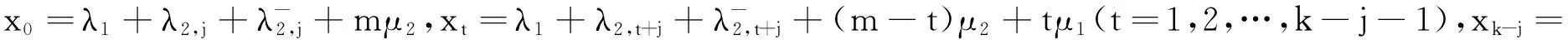
2.2 平衡方程组求解

由系统中2类顾客的稳态分布P·j的存在性及唯一性，由式(1)、(2)和克拉默法则可知，矩阵Aj(j=0,1,…,k-1)必为非奇异的.

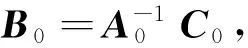
(3)

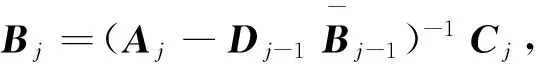
(4)

易知P·k=P0，k，令E0=1，由式(3)、(4)递推得

P·j=Ek-jP0，k.

(5)

(6)

将式(6)代入式(5)可求得系统中第2类顾客的稳态分布,

(7)

系统中第2类顾客的平均队长为

(8)

第2类顾客的溢出概率为

(9)

由于第1类顾客较第2类顾客具有强占优先权，且不受负顾客影响，故第1类顾客的稳态分布与只有一类顾客的经典的M/M/m/(k-m)排队相同[8]. 第1类顾客的稳态分布为

(10)

(11)

第1类顾客的平均队长

(12)

第1类顾客的溢出率

(13)

式(13)中P0由式(11)给出.

3 一个数值例子

利用参数m,k,λ1,λ2,μ1,μ2和式(3)～(13)用matlab编程.取m=3，k=8，λ1=λ2=0.7,μ1=μ2=0.3,可得系统中第2类顾客的稳态分布如表1所示.

由式(8)和(9)得稳态下第2类顾客的平均队长和溢出率分别为E(L2)=3.795 9，r2=0.253 3.

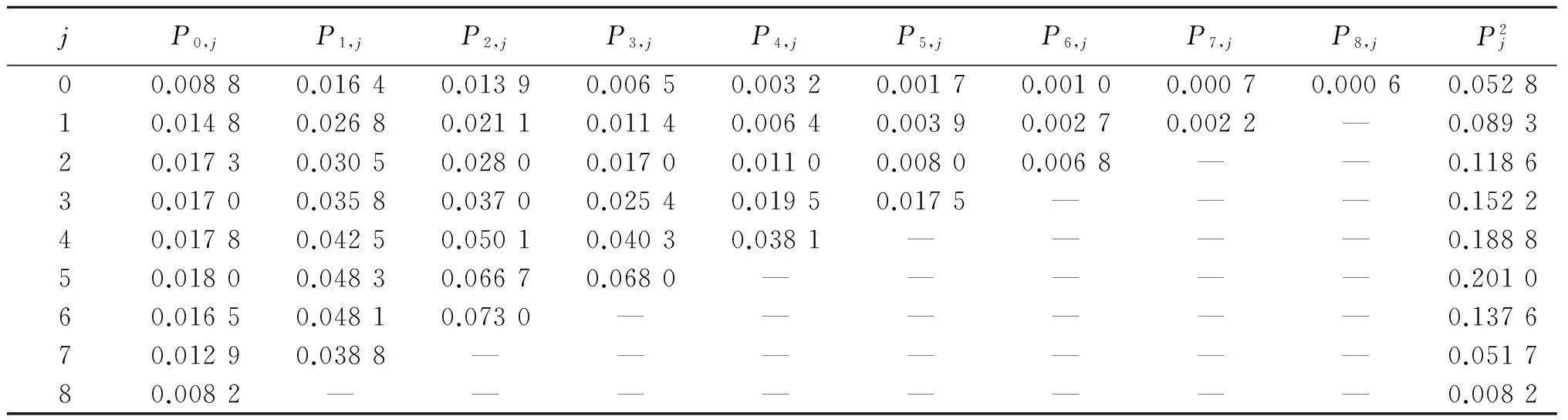
表1 系统中第2类顾客的稳态分布Tab.1 Stationary distribution of class 2 in the system

4 结束语

利用优先权排队可以为2类顾客提供不同的服务质量，考虑到现代通信中干扰信号的存在以及不同信号传输速率的变化，研究了依状态到达的正、负顾客对排队系统的影响.通过对系统中2类顾客平均队长的分析，可以估计2类顾客在系统中的延误时间；利用溢出概率可以改进服务台的服务率和等待轨道的容量，从而使系统得到优化，满足不同的需求，这对通信网络的发展能起到很大的推进作用.

参考文献：

[1] Gelenbe E，Glynn P，Sigman K.Queues with negative arrivals[J].J Appl Prob，1991，28(3)：245-250．

[2] Harrison P G，Pitel E.Sojourn times in single-server queues with negative customers[J].J Appl Prob，1993，30(4)：943-963.

[3] Miller D R.Computation of steady-state probabilities for priority queues[J].Operations Research，1981，29(6)：945-958.

[4] Steve D. An Eigen value approach to analyzing a finite source priority queuing model[J].Annals of Operations Research，2002，112(2)：139-152.

[5] 陈佩叔，朱翼隽，耿响.具有强占优先权的不耐烦顾客的排队模型[J].系统工程与电子技术，2008，30(6)：1069-1073.

[6] Demetres K，Nasredine T. An ME-based approximation for multi-server queues with preemptive priority[J]. European Journal of Operational Research，1994，77(3)：496-515.

[7] Indranil B，Raktim P.Average waiting time of customers in a priorityM/D/kqueue with finite buffers[J].Computers and operations research，2002，29(4)：327-339.

[8] 孙荣恒，李建平.排队论基础[M].北京：科学出版社，2002：44-54.