公路简支梁桥在车辆荷载作用下的动力响应分析
2012-05-22章长玖王贵春
章长玖, 王贵春, 陈 淮
(1. 郑州大学 土木工程学院 河南 郑州 450001; 2. 郑州新开元路桥工程咨询有限公司 河南 郑州 450016)
0 引言
车辆与桥梁的动力相互作用是一个复杂的课题,很多学者对其进行了研究,并取得了重要成果[1-3].早期研究主要采用经典的方法,常把车辆简化为移动常力、移动质量或移动车轮加簧上质量等简单模型[4-5].文献[6]比较了以上3种模型,提出了一些有价值的建议.但这些简化方法不能考虑复杂的实际情况.目前常用的方法是分别建立多刚体车辆模型、桥梁有限元模型及其各自的振动微分方程,再根据车辆和桥梁的几何相容条件和彼此之间作用力相等的原则形成车桥系统耦合振动微分方程,并求解,得到车辆与桥梁的动力响应[7-9].本文基于有限元通用分析软件ansys的二次开发来实现公路桥梁车桥耦合振动微分方程的求解过程,从而进行复杂的车桥耦合振动分析.
1 车桥耦合振动微分方程的建立
1.1 车辆动力分析模型
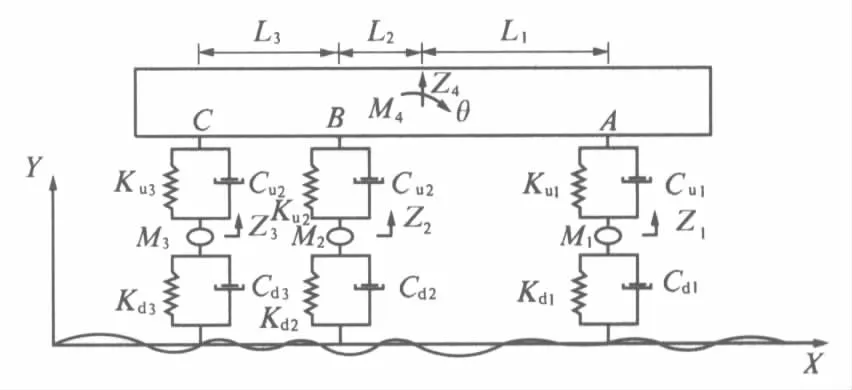
图1 车辆模型Fig.1 Vehicle model
车体、构架及轮对各部件沿车辆运行方向的纵向振动(伸缩)对桥梁的竖向和横向振动影响甚小,车辆竖向与横向振动之间的耦合效应较弱.本文研究车桥的系统的竖向振动,考虑车体的俯仰和浮沉、3个车轮的浮沉自由度,建立了具有5个自由度的车辆模型.其中把悬架和轮胎模拟成线性弹簧和阻尼器,质量集中在车轴处.车辆简化模型如图1所示[8]. 根据d’Alembert原理,可以建立车辆振动微分方程,其矩阵形式为
式中,[Mv]、 [Cv]和[Kv]分别为车辆的质量矩阵、阻尼矩阵和刚度矩阵;{Pv}为车辆的整体外力向量;{Zv}代表车辆5个自由度的位移向量.
1.2 桥梁动力分析模型
根据结构动力学和有限元理论,可建立桥梁结构振动微分方程,其矩阵形式为
式中,{Zb}为桥梁位移向量;[Mb]、[Cb]和[Kb]分别为桥梁的质量矩阵、阻尼矩阵和刚度矩阵;{Pb}为桥梁整体外荷载向量.
1.3 车桥系统动力方程的数值解法
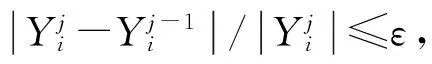
2 路面不平顺的数学模拟
路面不平顺是影响车桥系统振动的重要因素之一,本文按照三角级数法对路面不平顺进行模拟[10].利用matlab平台编制了模拟路面随机不平顺的程序,再现了随机不平顺路面.图2是对国标A,B,C,D级路面进行时域仿真得到的路面不平顺样本函数.
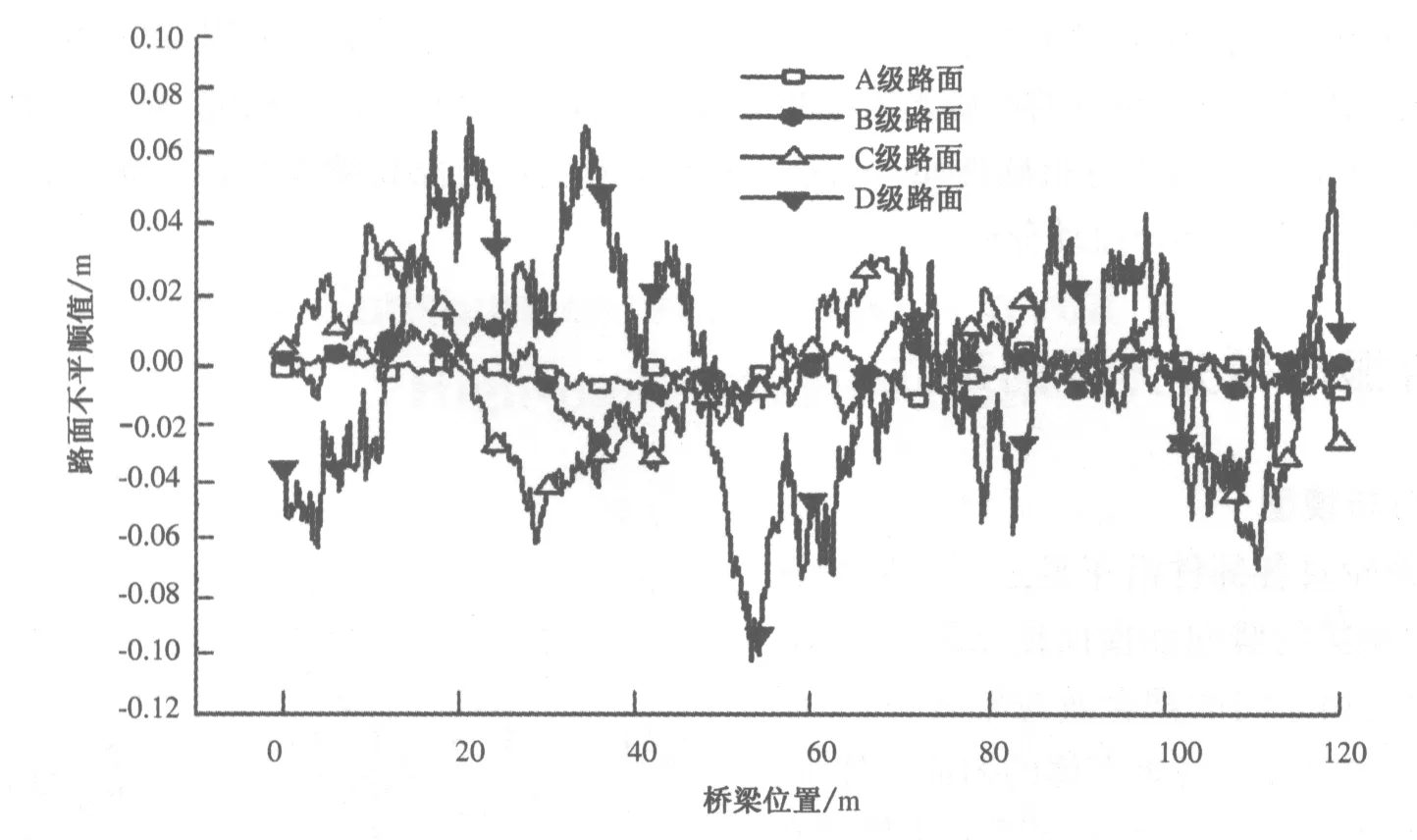
图2 路面不平顺曲线Fig.2 Road roughness curves
3 车桥耦合振动的数值分析
利用有限元软件ansys的二次开发APDL语言编写了车桥耦合系统迭代计算的命令流,计算了路面不平顺、车重、车速、车辆悬架刚度、车辆悬架阻尼、轮胎刚度和轮胎阻尼等因素对桥梁动力响应的影响.
车辆参数为[11]:
M1=500 kg,M2=1 450 kg,M3=1 450 kg,M4=28 500 kg,
Ku1=1 577 000 N/m,Ku2=4 724 000 N/m,Ku3=4 724 000 N/m,
Cu1=112 000 kg/s,Cu2=334 200 kg/s,Cu3=334 200 kg/s,
Kd1=3 146 000 N/m,Kd2=4 724 000 N/m,Kd3=4 724 000 N/m,
Cd1=13 300 kg/s,Cd2=10 000 kg/s,Cd3=10 000 kg/s,
Iθ=2.86×104kg·m2,L1=3.8 m,L2=0.4 m,L3=1.2 m.
当考虑不同车重的时候,需要对M4进行调整.桥梁参数为:跨径L=32 m,单位长度质量m=5.41×103kg/m,抗弯刚度EI=3.5×1010N·m2.
3.1 路面不平顺对桥梁动力响应的影响
图3为车辆以30 m/s的速度分别通过不同等级桥面时桥梁跨中节点位移、加速度的时程曲线.从图中可以看出,随着路面等级的恶化,桥梁的动力响应都成倍地增大.路面等级由A级降至D级时,桥梁跨中位移、速度、弯矩和剪力的最大值分别增大了7.82倍,8.01倍,8.24倍和8.02倍.
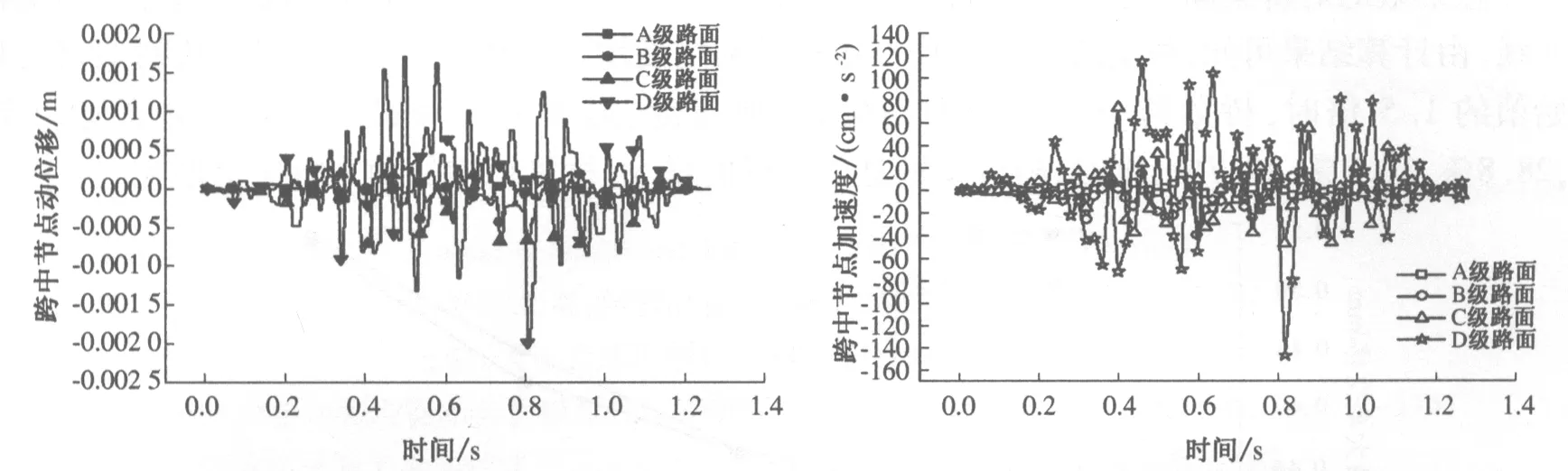
图3 车速为30 m/s时桥梁跨中动力响应时程曲线Fig.3 Time history curves of dynamic response of bridge at the midpoint of the span when the vehicle velocity was 30 m/s
3.2 车速和车重对桥梁动力响应的影响
为了研究车速对桥梁竖向位移的影响,分别取车速为10,20,30,40,50 m/s等5种情况进行计算.限于篇幅,仅给出不同路面等级下桥梁跨中节点最大位移和加速度随车速的变化曲线,如图4所示.
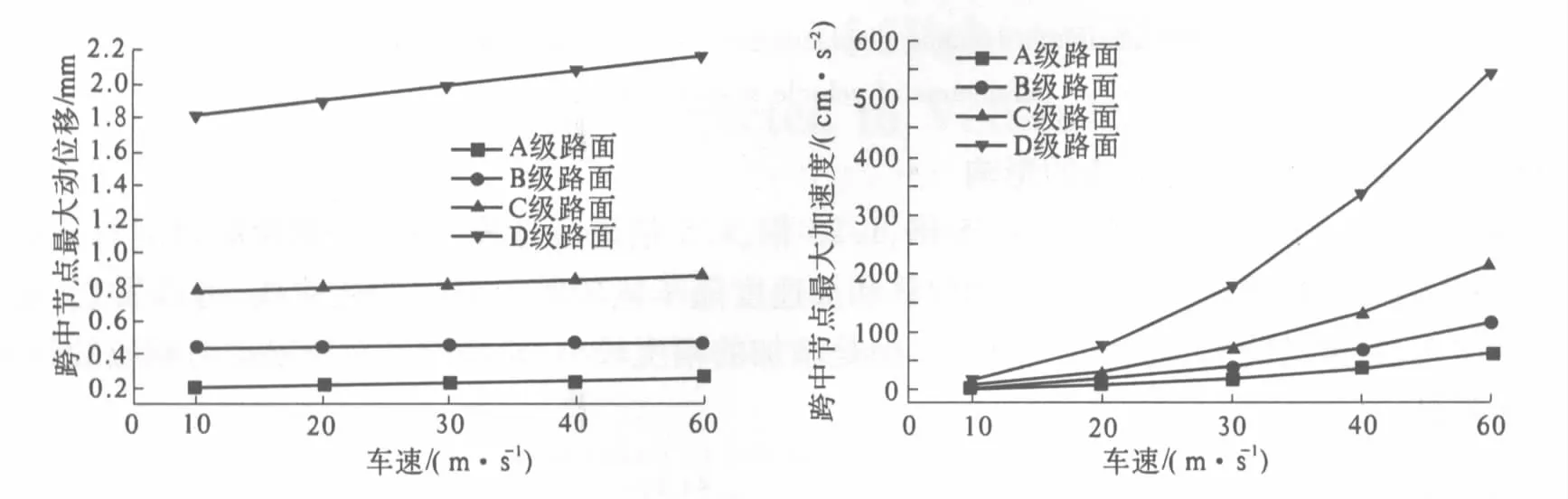
图4 桥梁跨中最大动力响应随车速的变化Fig.4 Variation of the maximum responses of bridge at the midpoint of the span with the vehicle velocity
从图4中可以看出,对每一种路面,桥梁结构的动力响应都随车速的提高而增大,路面等级越差,桥梁动力响应对车速的反应越明显,其中,车速对桥跨中点加速度影响很大,在A,B,C,D各级路面不平顺的激励下,车速在50 m/s时桥梁跨中最大加速度值与车速为10 m/s时的值之比分别为31.8,27.6,28,29.8.
影响车桥耦合振动的因素很多,本文以车速为30 m/s、路面等级为B的情况为例,研究了一些参数对桥梁动力响应的影响.分别取20,24,28,32,36,40 t共6个等级进行车重对桥梁动力响应影响的研究.图5给出了桥跨中点最大动位移和加速度随车重的变化曲线,可以发现,车重引起的桥梁静力响应远大于其引起的动力响应,车重对桥梁动力响应的影响较小.
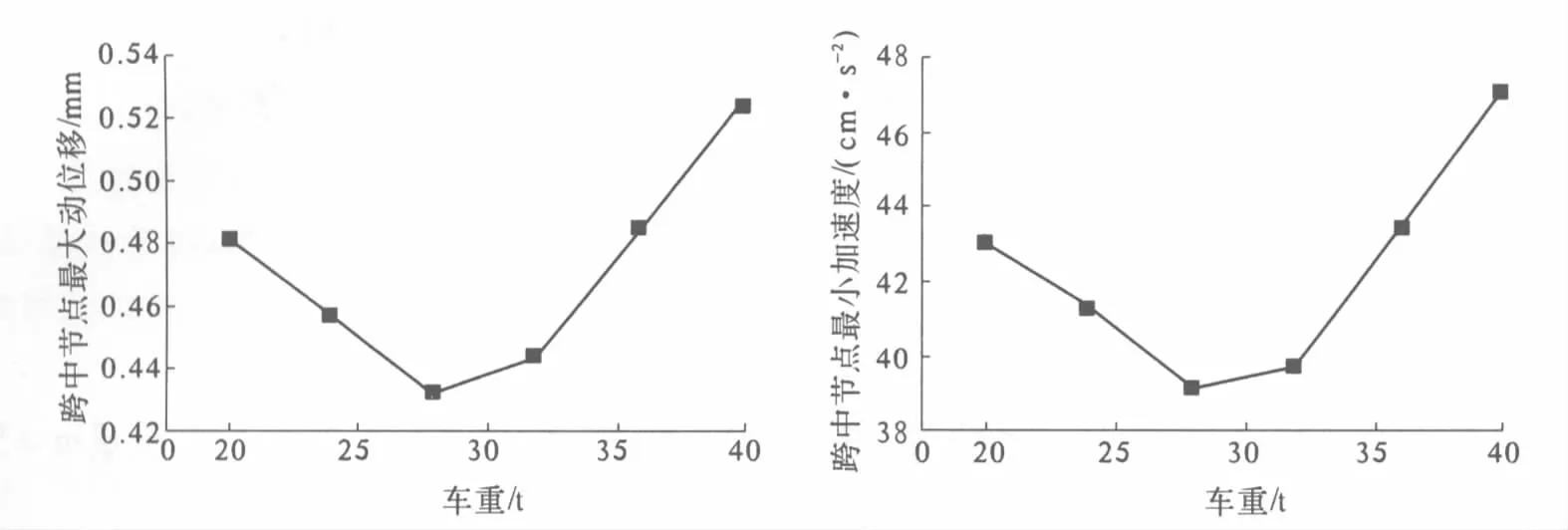
图5 桥梁跨中最大动力响应随车重的变化Fig.5 Variation of the maximum responses of bridge at the midpoint of the span with the vehicle weight
3.3 车辆悬架参数对桥梁动力响应的影响
分别取车辆悬架刚度和车辆悬架阻尼初始值的0.5倍,0.75倍,1.25倍,1.5倍进行计算,得出了车辆悬架刚度和悬架阻尼对桥梁动力响应的影响.图6给出了桥梁跨中节点最大动位移随车辆悬架刚度和阻尼的变化曲线.由计算结果可知,桥梁跨中动力响应随车悬架刚度增加而增大,当悬架刚度从初始值的0.5倍增至初始值的1.5倍时,桥梁跨中节点最大动位移、加速度、最大剪力和最大弯矩增加的幅度分别为27.1%,28.8%,16.7%,29.7%.同时,随着车辆悬架阻尼的增大,桥梁结构的动力响应也增大.
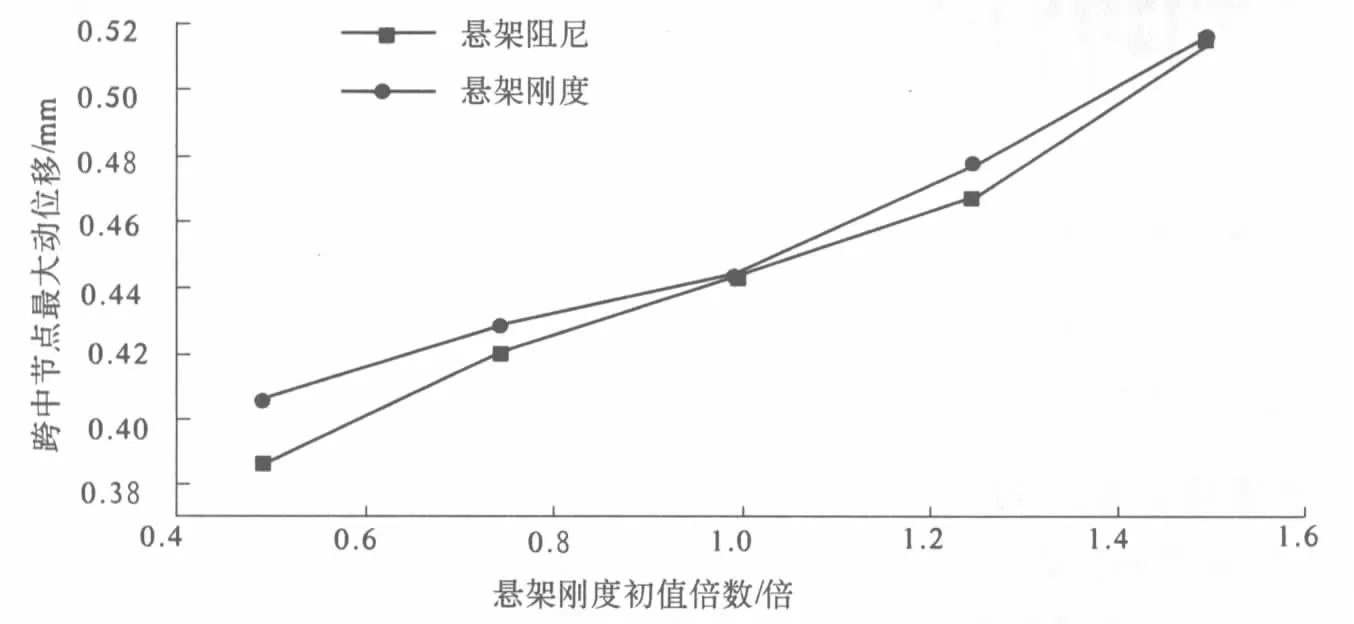
图6 桥梁跨中最大动位移随车辆悬架参数的变化Fig.6 Variation of the maximum dynamic displacements of bridge at the midpoint of the span with the parameters of vehicle suspension system
3.4 车辆轮胎参数对桥梁动力响应的影响
取车辆轮胎阻尼初始值的0.5倍,0.75倍,1.25倍,1.5倍进行计算,得出车辆轮胎阻尼对桥梁动力响应的影响,图7给出了桥梁跨中节点最大动位移和加速度随车辆轮胎阻尼的变化曲线.可以发现,随着车辆轮胎阻尼的增大,桥梁结构的动力响应也增大,但是增加的幅度较小.轮胎刚度对桥梁动力响应的影响很小,变化规律不明显.
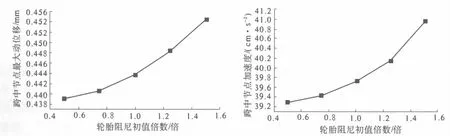
图7 桥梁跨中最大动力响应随车辆轮胎阻尼的变化Fig.7 Variation of the maximum responses of bridge at the midpoint of the span with vehicle tire damping
4 结论
为了研究公路简支梁桥的动力性能,利用有限元软件ansys完成了复杂车辆模型的车桥耦合振动分析,研究了路面不平顺、车重、车速、车辆悬架刚度、车辆悬架阻尼、轮胎刚度和轮胎阻尼等因素对桥梁动力响应的影响.结果表明:路面等级对桥梁结构动力响应的影响最为明显,当车速为30 m/s时,路面等级由A级降至D级时,桥梁跨中动位移、加速度、弯矩和剪力的最大值分别增大了7.82倍,8.01倍,8.24倍和8.02倍;随着车速的增加,桥梁结构动力响应都增大,其对加速度的影响最为明显;车重对桥梁的动力响应的影响相对较小;随着车悬架刚度和悬架阻尼的增加,桥梁动力响应都增大;车轮胎刚度和轮胎阻尼对桥梁动力响应的影响很小,基本可以忽略不计.
参考文献:
[1] Wu S Q, Law S S. Dynamic analysis of bridge-vehicle system with uncertainties based on the finite element model[J]. Probabilistic Engineering Mechanics, 2010, 25(4):425-432.
[2] Animesh D, Anjan D, Sudip T. Efficient dynamic analysis of cable-stayed bridges under vehicular movement using space and time adaptivity[J].Finite Elements in Analysis and Design, 2004, 40(4):407-424.
[3] Michaltsosa G T, Sarantithoub E, Sophianopoulosb D S. Flexural-torsional vibration of simply supported open cross-section steel beams under moving loads[J]. Journal of Sound and Vibration, 2005, 280(3):479-494.
[4] 夏禾.车辆与结构动力相互作用[M].北京:科学出版社,2002:140-146.
[5] 宋一凡.公路桥梁动力学[M].北京:人民交通出版社, 2000:74-94.
[6] 肖新标,沈火明.3种车桥耦合振动分析模型的比较研究[J].西南交通大学学报,2002,39(2):172-175.
[7] 王贵春.大跨度铁路斜拉桥车激振动线性及非线性分析[D].北京:铁道部科学研究院,1996.
[8] 章长玖.公路桥梁车桥耦合振动分析[D].郑州:郑州大学,2010.
[9] 王凌波,贺拴海,蒋培文.基于车桥耦合振动的桥梁检测方法研究[J].郑州大学学报: 工学版, 2011, 43(1):46-49.
[10] 星谷胜.随机振动分析[M].常宝琦,译.北京:地震出版社,1979:47-54.
[11] 黄新艺.混凝土连续曲线梁桥在车辆荷载作用下的动力响应研究[D]. 哈尔滨:哈尔滨工业大学,2008.
