压差方程的广义黎曼问题格式

王保军， 杨永举， 王顺钦， 王景泉， 职占江

(1.南阳师范学院 数学与统计学院 河南 南阳 473061；2.河南大学 数学系 河南 开封 475001)

0 引言

微分方程的黎曼问题是最简单、最经典的初值问题，Riemann、Von Neumann和Courant等著名数学家对此都做了深入研究；张同等利用相平面分析法专注于空气动力学中的黎曼问题[1]．在数值计算方面，Godunov构造了求解黎曼问题的Godunov格式[2]；Ben-Artzi等以Godunov格式为基础，引入二阶Godunov类型格式并研究了反应流的广义黎曼问题[3]；文献[4]利用解析的方法对中心疏散波重解，构造了可压流体方程组的广义黎曼问题(GRP)格式．GRP格式关于时间和空间都是二阶的，是真正意义上的二阶数值格式．

压差方程最初是李荫藩和曹亦明在用流体矢量分裂法[5]对欧拉方程组做数值分析时引入的，是欧拉方程的一种特殊形式[6]．本文研究一维压差方程的简化形式

(1)

其中,U=(u,E)T，F(U)=(p,pu)T,E=p+u2/2，x和t分别为空间变量和时间变量[7]．

1 符号说明

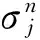
(2)

其中，

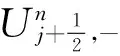
2 简单波的重解

2.1 中心疏散波的重解

(3)

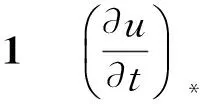
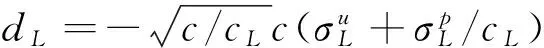
图1 压差方程广义黎曼问题伴随黎曼问题的波形 Fig.1 Wave pattern of associate Riemann problem for the general Riemann problem of pressure gradient equations(PGE)

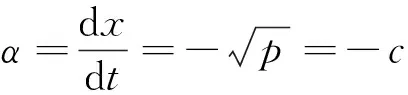
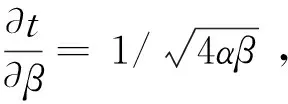
故

(4)

因为ψ在β-曲线方向不发生变化，所以

(5)

(6)

(7)

利用(5)、(6)和(7)，可得

(8)

另一方面，

(9)

将(4)和(9)代入(8)即得引理1的结论．

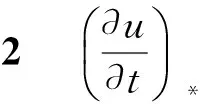
2.2 激波的重解

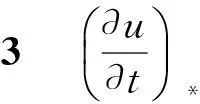
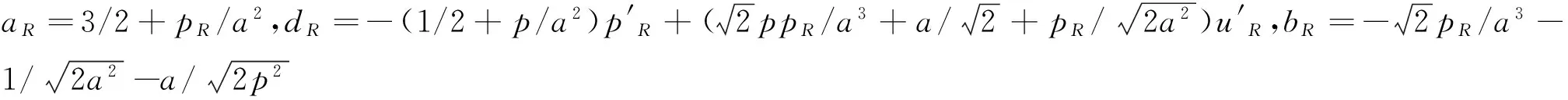
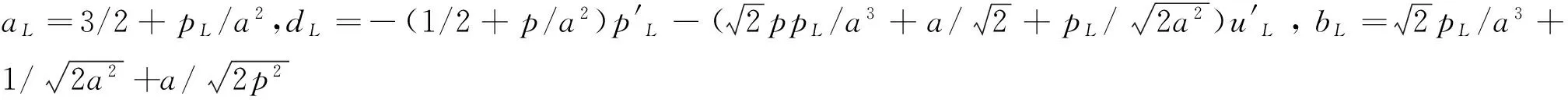
3 GRP格式的计算

GRP格式的计算过程包括4个步骤：

1)对初值进行分段线性逼近，求解黎曼问题以确定

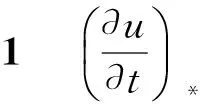
得到，其中，aL,bL,dL,aR,bR和dR由压差方程的黎曼解的波形和引理1～4确定．

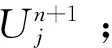
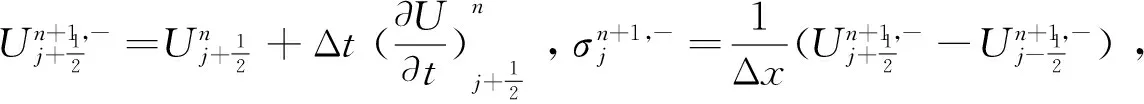
确定，α为常数且α∈[0,3)．

4 数值试验

利用GRP格式计算一维压差方程的经典黎曼问题，部分结果如图2和图3所示．数值实验表明压差方程的GRP格式有很高的精度，但不能从本质上克服Godunov类型格式的缺陷[8-9]．文[9]证明了Godunov格式的这个缺陷来自它本身，可知Godunov类型格式对压差方程只包含强简单波的黎曼解有很好的性质，而对包含弱简单波的黎曼解则是不适用的．

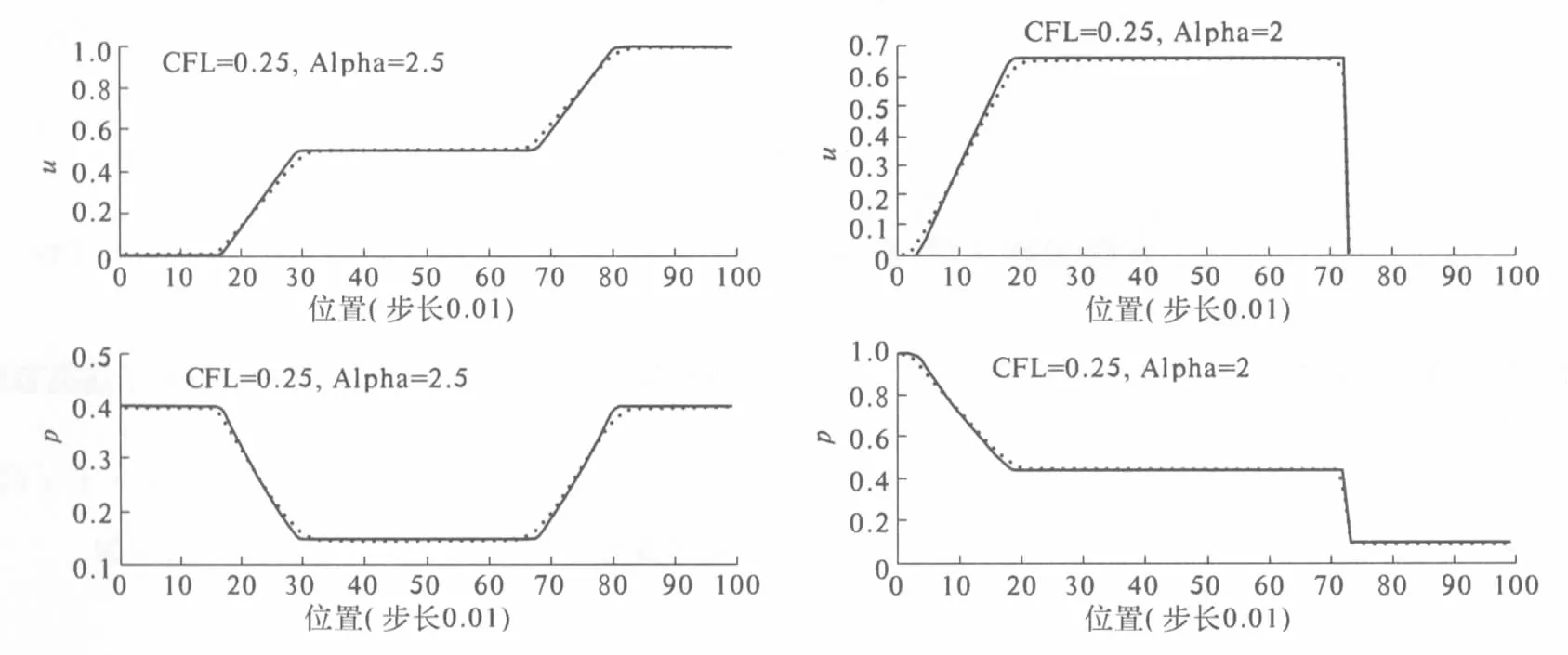
图2 压差方程仅含有强简单波的黎曼解(实线)及GRP格式计算的数值解(点)的比较Fig.2 Comparison of true-solution without weak waves and numerical solution computed by GRP scheme for PGE

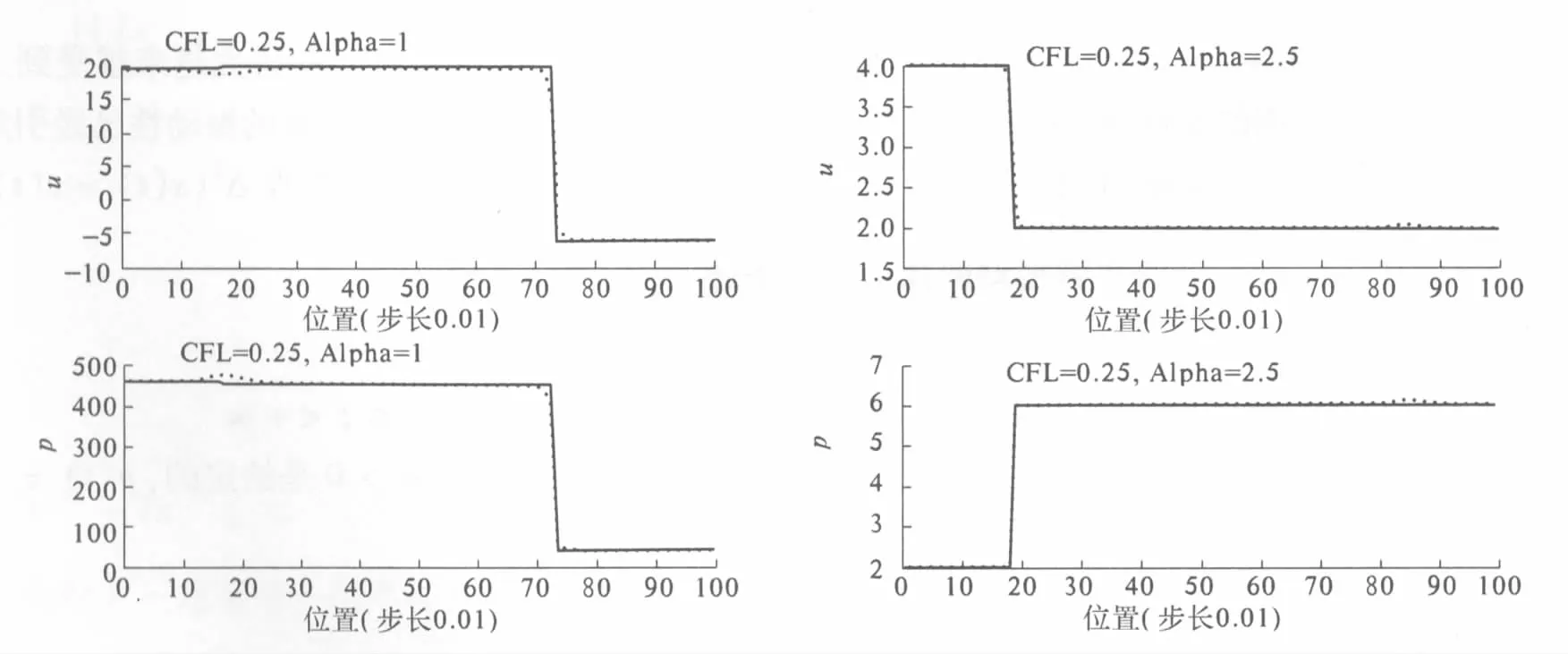
图3 压差方程含有弱简单波的黎曼解(实线)及GRP格式计算的数值解(点)的比较Fig.3 Comparison of true-solution containing weak waves and numerical solution computed by GRP scheme for PGE

参考文献：

[1] Zhang Tong，Xiao Ling．The Riemann Problem and Interaction of Waves in Gas Dynamics[M]．New York: Longman Scientific & Technical, 1989:3-161.

[2] Godunov S K. A finite difference method for the computation of discontinuous solutions of the equations of fluid dynamics[J]. Math Sb, 1959, 47(1):357-393．

[3] Ben-Artzi M. The generalized Riemann problem for reactive flows[J].J comput Phys,1989,81(1):70-101．

[4] Ben-Artzi M，Li Jiequan， Warnecke G. A direct Eulerian GRP scheme for compressible fluid flows[J].J comput Phys, 2006,218(1):19-43．

[5] 苏克勤，邢家省，冯仁忠．结合矢通分裂的差分格式[J]．郑州大学学报：理学版，2008,40(2):39-41.

[6] Li Yinfan, Cao Yiming. “Large-particle” difference method with second order accuracy in gas dynamics[J]. Scientia Sinica: Series A, 1985, 28(10): 1024-1035．

[7] Li Jiequan, Zhang Tong, Yang Shuli. The Two-dimensional Riemann Problem in Gas Dynamics[M]. New York: Longman Scientific & Technical, 1998:157-159．

[8] 王保军，王景泉．压差方程的HLL逼近Riemann格式[J]．南阳师范学院学报，2008,7(3):26-28．

[9] 王保军，张炳侠．压差方程的Godunov格式[J]．南阳师范学院学报，2008,7(12):10-13．