基于BP神经网络的市政工程造价预估研究
2012-05-15郝艳芬张军朝陈俊杰赵荣香
郝艳芬,张军朝,陈俊杰,赵荣香
(1.太原市建设工程预结算审核中心,太原,030002;2.太原理工大学 计算机科学与技术学院,太原030024;3.山西太原天地方圆电子科技有限公司,太原030024)
工程造价预估是项目建设前期造价控制的重要手段,对于施工过程中的工程结算和最终工程总决算都起着至关重要的作用。建立工程造价预估模型,较为准确地预估工程造价,具有十分突出的研究价值,社会效益和经济效益明显。
市政工程是现代化城市建设的主要内容之一。道路工程、地铁工程、给排水工程、热力燃气管道工程、路灯工程、电力电缆等市政工程项目各具特点,对市政工程的造价均有不同程度的影响,有的分项工程甚至决定着市政工程的造价。因此,将这些分项工程的各自工程特点与造价联系起来,建立一种“工程特征——工程造价”的对应关系系统,对工程造价的管理具有十分重要的意义[1]。
市政工程造价预估具有高度非线性特征,其造价预估结果受到项目特征和工作内容等因素的影响,用传统的方法很难建立精确的数据模型,很难建立一种“工程特征——工程造价”的对应关系,不能满足准确预估市政工程造价的需求,工作效率低下。
近年来,随着人们对人工神经网络系统的深入研究,其在各行业也得到了一定应用[2],本文引进BP神经网络,以某市政管道安装工程为例,探讨BP神经网络在造价预估中应用,为其推广应用提供参考。
1 市政排水管道工程项目造价特征分析
1.1 工程分类
市政排水工程由污水、雨水管道工程和污水处理构筑物工程等组成。市政排水管道的分类有多种,常见的有按污水及雨水排放方式和按管道材料分类两种,其中,按雨水、污水排放方式可以分为合流制与分流制两种,按材料分类可以分为钢筋混凝土管道和HDPE双壁波纹塑料管道等。实践证明,按管道材料分类更能够方便对工程造价的预估。
本文以某市2010年度完工的太原市16条市政排水工程为样本,雨水、污水管道类别是分流制的单雨单污形式钢筋混凝土管道,利用该样本进行研究。
1.2 市政排水管道工程项目造价特征
市政排水管道工程包含很多内容,主要有:挖填土方、管道基础、检查井、雨水篦等。这些分项的各方面因素均影响着排水工程的总造价,这类因素很多,抓住主要因素能够方便造价的预估。
本文根据经验,筛选了9个特征因素,如表1市政管道工程造价特征因素所示,把握这些主要因素就能够很大程度上方便工程造价的预估。

表1 市政管道工程造价特征因素
以这9个因素为输入向量,我们首先将某市2010年度完工的16条市政排水工程相关对应的造价数据整理出来,依次输入,通过BP神经网络模型输出得到排水管道延米长造价(C),具体如表2造价样本数据库所示。
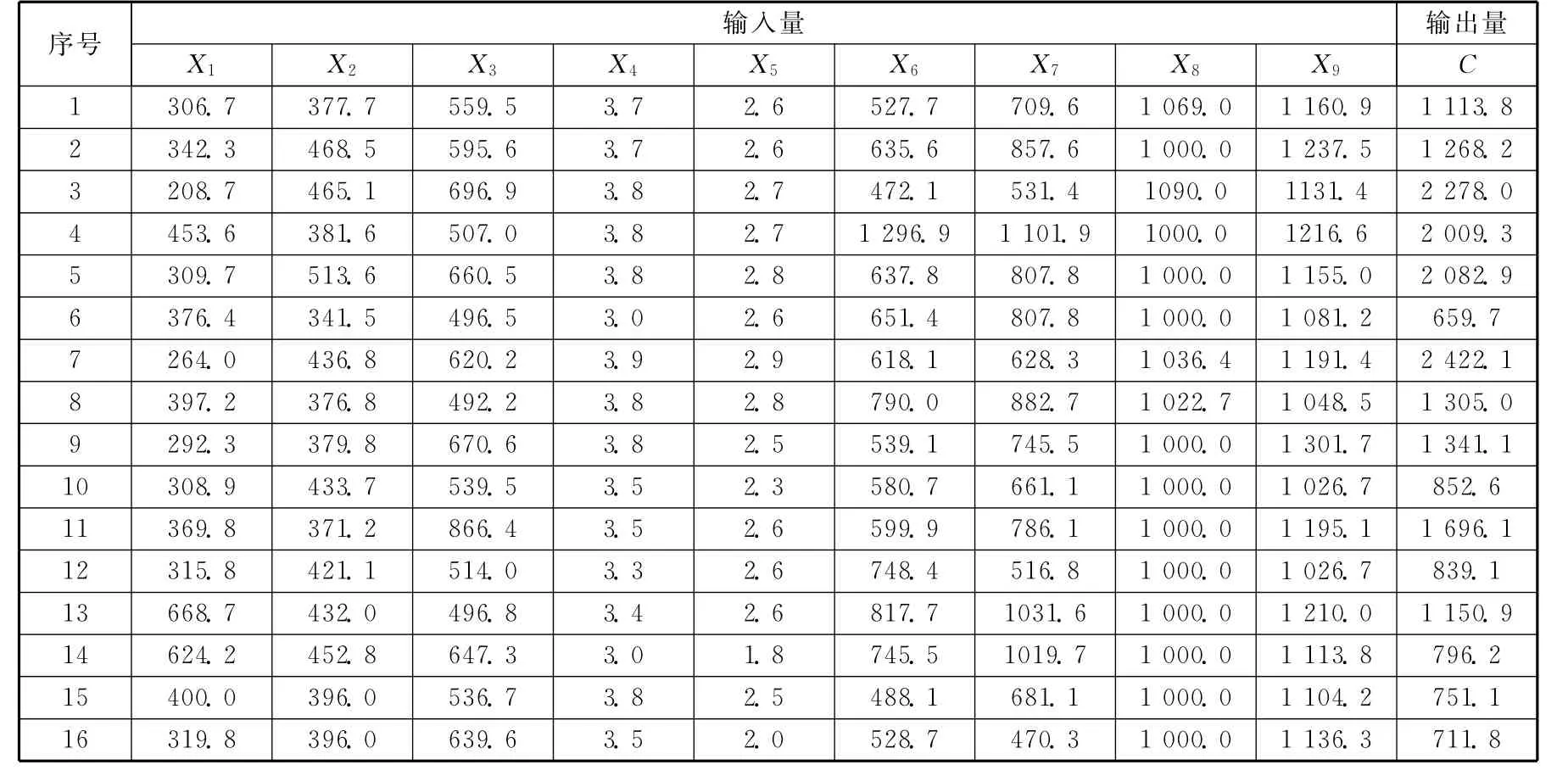
表2 造价样本数据库
2 基于神经网络的工程造价估算模型的建立
目前神经网络的研究已取得很大的成就,有BP模型、波尔茨曼机模型、多层感知级模型、自组织网络模型、连接型网络模型等等。其中BP多层前馈网模型是应用最为广泛的一种。本文采用单隐层BP多层前馈网模型建模。
2.1 单隐层BP多层前馈网数学模型
BP多层前馈网具有输入层、隐层、输出层节点,其中隐层有单隐层和双隐层之分。单隐层BP多层前馈网又叫三层前馈网,其输入向量为X=(x1,x2,x3,…,xi,…xn)T,输出层输出向量为C=(c1,c2,c3,…,cj,…cm)T,隐层输出向量为:M=(m1,m2,m3,…,mk,…ml)T,在输入层向量和隐层输出向量中加入x1=-1和c1=-1,得到输入层和隐层的阈值。输入层到隐层的权值矩阵为V=(v1,v2,v3,…,vk,…,vl)T,列向量vk为隐层第k个神经元对应的权向量;隐层到输出层的权值矩阵为:W=(w1,w2,w3,…,wj,…wm)T,列向量wj为隐层第j个神经元对应的权向量。各层信号之间的数学关系如下:
输出层
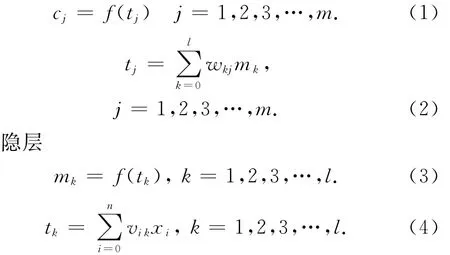
选取单极性Sigmoid函数

作为以上公式中节点作用的转移函数,该转移函数具有连续、可导的特点。公式(1)—(5)组成了单隐层BP多层前馈网的数学模型。
2.2 基本原理概述
逼近原理是神经网络法的基础,依据神经网络函数的逼近法则对复杂的非线性函数进行模拟映射[3]。故在对工程造价进行预估时,首先要弄清楚工程造价的特征因素种类和数量,利用影响因素和造价资料建立起一个m×n的空间映射式(6)所示(其中n和m分别为工程造价影响因素和已有造价资料的个数,均≥1)。那么,本文按表2中9个影响因素进行造价预估,其特征因素-工程造价映射关系图就如式(7)(其中m=16,n=9)所示。
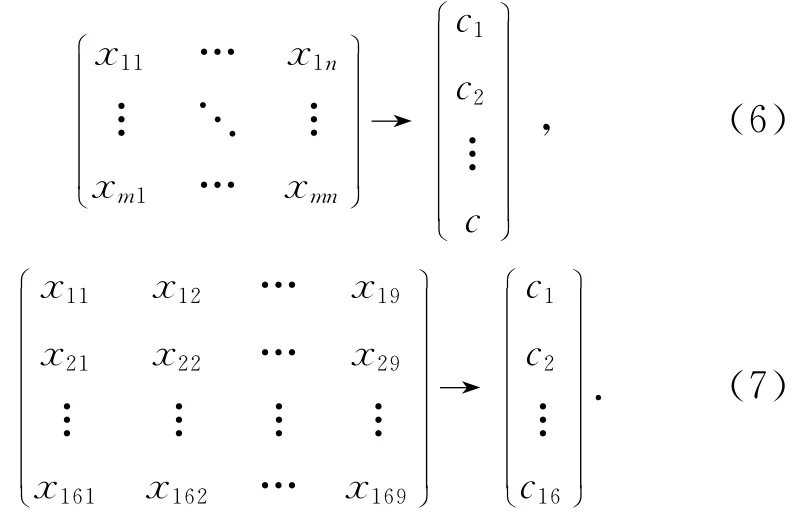
以工程的特征因素作为神经网络的输入向量,将所需的工程造价作为神经网络的输出向量,通过将已有相似工程的造价信息进行输入,训练网络函数,使函数不断修正改进,从而实现输入空间(工程特征X)到输出空间(工程造价C)的映射,随着更多造价信息的输入,函数训练的次数不断增多,网络模型估算的准确性不断提高,这就是基于神经网络的工程造价估算模型[4]。
2.3 BP神经网络估算模型的设计
BP神经网络估算模型建立的关键是设置隐层和隐节点,同时要确定输入输出的节点个数。
有研究证明,利用单隐层的前馈网可以实现对所有连续函数的映射,而使用双隐层的前馈网可以实现对不连续函数的映射。这里利用BP神经网络对工程造价的预估要实现的是对“Sigmoid”的映射,而“Sigmoid”函数为非线性连续函数,故只需设置一个隐层。
当隐层数列确定后,需要确定隐节点的个数,这需要利用试凑法,首先设置隐节点数的初始值,然后逐渐增加,通过对网络训练的结果确定最佳隐节点数。这里设置的隐节点数的初始值为3,然后依次增加节点数,比较训练结果误差,通过试算,发现节点数为4时,误差最小,因此最优节点数为4。那么,本文的神经网络模型就如图3所示。
3 市政管道安装工程造价估算
按图3建立好BP神经网络模型,借助电脑程序,不断输入数据,藉此对模型进行反复训练和检验。本文利用Matlab软件,多次调用软件自带函数进行神经网络模型的模拟编程。利用Matlab软件编制程序,实现对表2数据库的训练和仿真测试[5]。
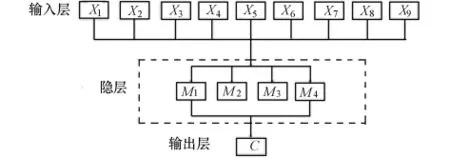
图3 BP神经网络估算模型
程序 中,先 后 采 用 了 “Logsig”、“Purelni”、“Trainlm”三种函数,分别实现神经元隐层模拟、神经元输入以及神经网络权值和阀值的调整。其中“Logsig”函数是一种对数“Sigmoid”型传递函数,属于非线性作用函数;“Purelni”函数是一种纯线性传递函数;“Trainlm”函数是以最小二乘法为基础的反向传播算法程序[6]。
通过以上程序实现了BP神经网络模型的训练和调整,关于模型的准确性,采用了“Sim”仿真函数,通过仿真测试,得出模型的均方误差在容许范围内。最后,采用“Postmnmx”函数处理输出结果,录入估算值数据库GS。如表3所示,将GS与实际值数据库YS进行比较,计算第15,16个样本预估造价与实际值的误差(≤10%)。结果显示,预估结果误差在容许范围内,预估结果可以接受。
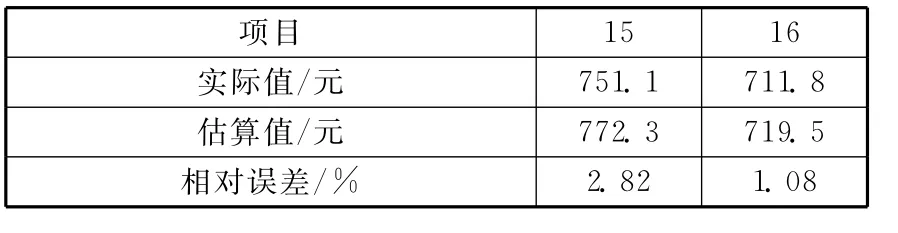
表3 估算值与实际值对比表
4 结语
1)利用BP神经网络原理进行工程造价估算的方法是合理可行的。
2)由于网络的复杂性,因此样本的收集是关键,样本最好多为同一地区、同一时期的工程数据,且样本数量要足够多。
3)适当利用数学软件可以使估算过程规范化程序化,并且能够节约时间,提高效率。
[1] 董士波.全寿命周期工程造价管理研究[D].哈尔滨:哈尔滨工程大学,2003.
[2] 张军朝.太阳能路灯系统的仿真研究[J].计算机仿真,2011,28(4):328-331.
[3] 李文华,李玉文.基于人工神经元网络的建筑工程造价预测方法研究[J].中国管理科学,1999(12):19-34.
[4] 胡志根,梅阳春.工程项目造价快速估算方法研究[J].基建优化,1995,16(3):22-29.
[5] 葛哲学,孙志强.神经网络理论与Matlab R2007实现[M].北京:电子工业出版社,2007.
[6] 张良均,曹晶.神经网络实用教程[M].北京:机械工业出版社,2008.
