频域子空间模态参数辨识的改进算法

马立元，李永军，王天辉，李世龙

（军械工程学院 导弹工程系，石家庄050003）

作为子空间模态参数辨识算法的一个分支，频域子空间辨识算法出现较晚，最早由T.Mckelvey等人于1994年提出。对于复杂结构，其输出点较多，关心的频域范围较广，因此导致非常大的计算量。很多情况下，实验室的设备很难满足这种大计算量的要求。为解决这一矛盾，笔者提出频域子空间辨识算法的改进方法，不需要采用滤波手段，能在不减少数据量的前提下，减小计算量，得到关注频域内的模态参数。

1 频域子空间模态参数辨识基本原理［1－2］

多自由度振动系统离散时间系统的状态方程描述为［3］

式中：ξk＝ej2πk／N为傅里叶算子；U、Y 分别为输入u、输出y的傅里叶变换。

则式（2）写成

由于Y、X和U均为复数，则上式可以写成

Re（·）表示复数的实部，Im（·）表示复数的虚部。

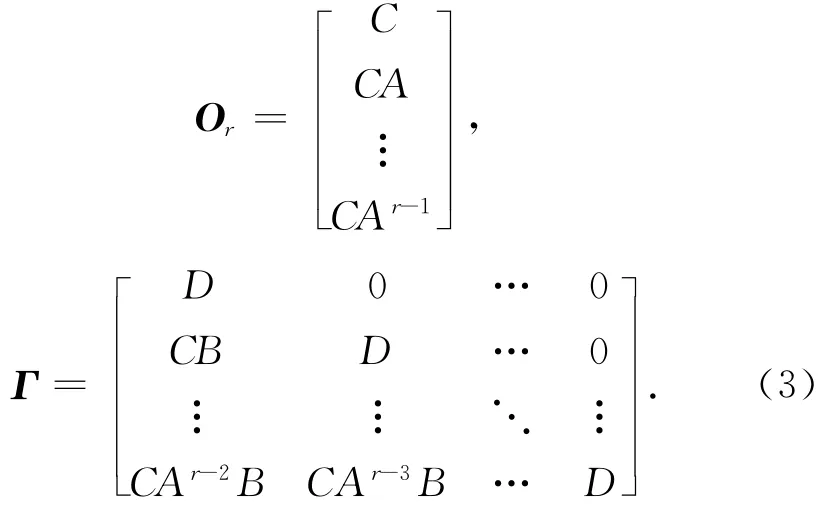
根据输出获得系统状态方程中的矩阵A、C的估计矩阵＾A和＾C，具体算法如下：

构建矩阵

式中：A／B表示矩阵A 到矩阵B 的行空间上的投影。对RT22进行奇异值分解

可得到Or的估计值

式中：n为模型的阶次，系统的阶次常根据Σ中较大的奇异值个数确定。

根据最小二乘法估计矩阵A，C

式中：上标“†”表示 Moore-Penrose逆；N0为输出点个数。

采用离散系统建模，模态频率、阻尼和振型的计算式如下［4］：

式中：λk为矩阵A的特征值；Ψ为矩阵A的特征向量。

2 分段频域子空间辨识算法

上述的频域子空间算法，频域子空间辨识方法中，矩阵Y和U的块行数q需要仔细考虑。为了能进行辨识计算，必须满足q≥n，n为系统阶次。经数值计算经验证明，对于小阻尼系统，q值取的较大为好。一般需要满足q≥10n［7］。而为了获得较为准确的傅里叶变换，又必须有足够大的数据长度。一般情况下，实验室设备无法满足要求。以某一梁结构为例，其输入点1个，输出点为5，在一台式计算机上进行计算，计算机参数为主频2.6GHz，内存4GB。当频域数据点超过2 500时，则产生了内存溢出问题。

为此，笔者提出了一种分段计算方法，以减小对计算设备要求。其方法如下：U（k）∈CN×l，Y（k）∈CN×L.分别表示时域输入输出数据u，y的离散傅立叶变换，N为采用点数，l为输入点数目，L为输出点数目。

将U，Y分成K 段，第i段为

Ni为该段内的频率点数。

当采用离散模型建模时，

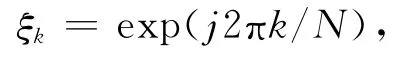
表示z域内单位圆上的某一点。对于第i段频域数据Ui和Yi，其对应的广义算子为

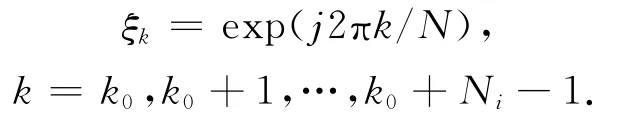
k0为该段的起始点在全部频率点中的排序序号。

其值为

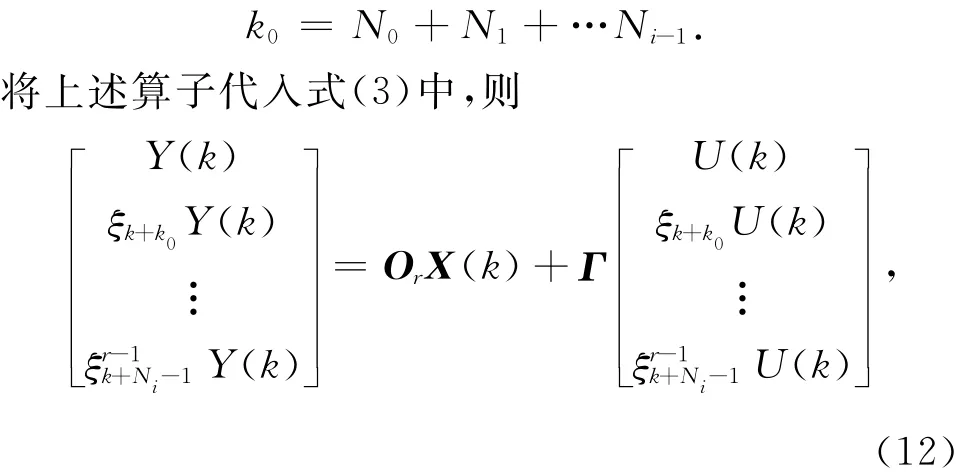
对上式按照频域子空间算法的一般算法进行模态参数辨识，则可获得在第i个频率段内的模态参数。将所有频率段内的模态参数聚集在一起，则构成系统的所有模态参数。

分段算法的理论证明如下：

式（5）可以写为

式中（·）i表示第i段数据分解结果。则

式（7）变为

可得到Or的估计值

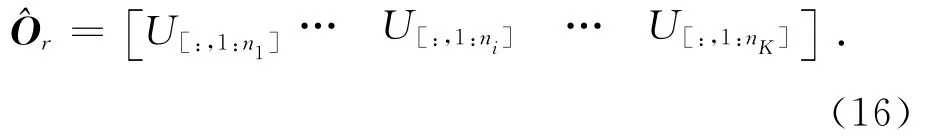
式中，ni为该频域段内系统阶次。

而对系统矩阵的估计为

因此，对频域分段辨识得到的特征值为系统矩阵特征值的一部分，辨识所得模态参数为系统在该频域段内的模态参数。但是，需要特别指出的是，在分段辨识模态参数时，因其只分析该段内的数据，系统的阶次将发生变化，需要重新确定系统阶次。

3 分段计算辨识矩阵与系统系数矩阵之间的关系

因分段计算得到的系统矩阵仅为某一频段辨识结果，因此，最终系统矩阵需要进行综合计算。设输入输出的傅里叶变换数据分成K段，第i段数据得到的系统矩阵为Ai、Bi、Ci、Di，则

式中（·）（i）表示第i段傅里叶变换数据。

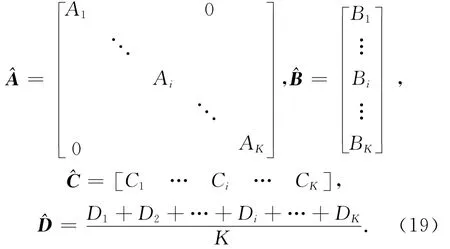
由上式可得最终辨识的系统矩阵为对D进行平均的原因是各个频域数据段辨识结果中的矩阵Di不受频域段的影响。可以认为D≈D1≈…≈Di…≈DK。

4 变截面轴上的应用

某装备的传动部件受环境、自身转速等因素影响，经常出现故障。为了减少故障率，要使传动轴的转速避开其固有频率，因此有必要对传动轴的模态参数进行辨识。

实验对象是一个横截面为方形的台阶轴结构，材料是45号钢，传感器及激励点如图1所示。由于该轴的对称性，可以只考虑其弯曲模态，减少传感器数量需求。

图1 变截面轴测点布置

在进行模态分析实验时，对实验对象采用力锤进行激振。采样频率为10 000Hz，每个响应信号取10 000个采样点。实验时利用动态信号测试仪测得响应数据，利用Matlab软件编程实现模态参数识别。系统阶次根据SVD分解结果，确定为4阶。

对采集到的数据进行傅里叶变换后，频域点分为3段，分别为：1—2 000点；2 001—4 000点；4 001—5 000点。有限元计算（FEM）能够使分析者对该框架结构的特征有初步了解，也可以为实验室的测试工作和参数辨识计算提供参考，使分析者在实验之前就能够大致掌握振型节点的所在之处，结构的基本振型等情况。对于小型金属结构，已经验证有限元计算结果的可靠性［5－6］。表1给出了分段计算辨识结果与有限元计算结果的对比。

表1 辨识结果与有限元结果比较

图2—图5列出了ANSYS计算的振型和分段频域子空间方法识别的振型对比。

通过表1和图2—图5对比发现，试验模态参数识别得到的各阶模态参数与有限元分析得到的分析模态参数基本一致，证明了本研究所采用的模态参数识别方法基本正确，所得的模态参数准确反映了该部件的动态特性。

图2 第1阶振型对比

图3 第2阶振型对比

5 结论

从频域子空间基本算法出发，提出了一种采用采用分段频域子空间的模态参数识别方法，其有效性及准确性被试验分析所证明。

图4 第3阶振型对比

图5 第4阶振型对比

经试验证明，在频域数据点数较小的情况下，该算法仍然能够获得相对准确的模态参数，从而能够减小计算量和对计算资源的需求。

［1］ 唐炜.飞机颤振模态参数识别方法研究［D］.西安：西北工业大学，2006.

［2］ Mckelvey T.Subspace Methods for Frequency Domain Data［A］.In Proceeding of the 2004American Control Conference［C］∥Boston，Massachusetts，USA，2004.

［3］ 常军.随机子空间方法在桥梁模态参数识别中的应用研究［D］.上海：同济大学，2006.

［4］ 樊江玲.基于输出响应的模态参数辨识［D］.上海：上海交通大学，2007.

［5］ 薛玮飞，张智，陈进等.空调配管模态仿真分析与实验研究［J］.机械科学与技术，2010，29（6）：822-825.

［6］ 孟杰，陈小安，陈锋.高速电主轴的试验模态分析［J］.机械设计，2009，26（6）：70-78.

［7］ Schoukens J，Pintelon R.Estimation of nonparametric noise models［C］∥IEEE Instrumentation and Measurement Technology Conference.Sorrento，Italy，2006.