土体沉降引起地下管线破坏的实验性研究
2012-05-15曾国红白晓红贺武斌
周 敏,曾国红,白晓红,贺武斌
(太原理工大学 建筑与土木工程学院,太原030024)
地下管道在城市生活中起着不可缺失的作用,随着城市的发展,城市地下管道系统也越来越庞大复杂,一旦发生破坏,对城市居民的生活将产生极大的影响,而且维修的工作也不容易进行。由于土层沉降而发生地下管线破坏变形屡见不鲜,通过实验模型对其进行模拟,可以得到土层沉降对于地下管线的影响破坏规律,以便在实际工程中采取相应的措施来保护管线,同时还可以为地下管线监视系统提供其所需要的管线破坏临界范围相关数据,从而可以及时地对将要破坏的管线进行维护和修理。一般对于工程实际模拟的实验理论基础是相似原理和量纲分析,其目的在于找到工程实际和物理实验模型的相似判据,以便确定出实验模型的尺寸、材料、受力等诸多方面的条件,从而建立与工程实际相似的实验模型,得出对实际而言有参考价值的数据和信息。
目前国内外学者对于相似理论有大量的研究,但主要是针对于流体领域,例如对于流体的相似研究,我们已经有了相当成熟的相似判据,包括雷诺数、弗劳德数、欧拉数、柯西数、韦伯数、斯特劳哈尔数等,这些相似判据可以清晰地判定流体试验与实际情况相似的程度[1-4]。对于非流体领域,前人也作了相关研究。胡云用量纲分析法对建立相似的物理模型进行了相关的讨论[5],李国梁、韩超等对深基坑的相似材料进行了研究分析[6],范鹤、刘斌等对高填土涵洞材料进行了相似研究[7]。太原市有关部门在进行城市地下管网一系列工作的同时,地下管网的监控系统需要有关于土层沉降引起地下管线变形破坏的一系列数据,以便加强预警监控功能。为了获取相关数据,运用物理实验模型对太原市管道埋置情况进行模拟便成为了一条行之有效的措施。笔者在前人的基础上,对于土体沉降引起地下管线变形破坏的实验模拟相似性作了进一步的分析和研究。
1 相似原理以及本实验相似原理思路的阐述
白金汉(Buckingham)定理[8]:当一个现象由n个物理量的函数关系f(x1,x2,x3,…,xm)=0来表示,且这些物理量在量纲上含有m个相互独立的量时,则能得到(n-m)个相似判据,这些相似判据满足的函数关系式g(x1,x2,x3,…,xn-m)=0等价于f(x1,x2,x3,…,xm)=0,从而可表征相似的物理现象。
如果两个系统拥有相同的相似判据,则这两个系统相似。相似的两个系统中各对应物理量的比值是无量纲的常数,称为相似常数。相似常数之间必定满足一定的关系,这种关系可以由相似判据得到,只要设计的模型与原型中相对应量的比值满足相似常数,则可以由模型模拟反映出原型的力学状态。
对于土体沉降这样复杂的物理现象,想要在理论上罗列出一系列可以精确表达这一物理现象的数学方程式是困难的,但只要我们知道哪些物理量在这一现象中起着重要的影响作用,利用量纲分析和相似原理对其加以分析就可以得到相应的相似判据,从而建立起具有实际意义的模型模拟实验。
在土体没有发生沉降时,土体和地下管道的整个系统处于稳定平衡状态;在随后的土体沉降过程中,土体发生了位移,呈现一种类似于流动的状态;在土体沉降稳定之后,管道产生了大变形或者发生破坏。高惠瑛、冯启民[9]针对土体沉降结束后,管道产生大变形的最终状态进行受力分析,朱庆杰等[10]用软件模拟了管土摩擦和管径对于地下管道的破坏作用,笔者参考前人的理论成果并加以进一步分析,挑选了对于土体沉降引起管线变形破坏这一现象产生重要影响的几个关键性因素,并对其进行了相似分析,得出了相似判据。
2 建立地下管线沉降破坏试验模型的依据
2.1 几何相似
在实验模拟中,我们首先要考虑的是实验模型和原型在几何尺寸上要达成一定的相似比例。在模拟实验中,上覆土埋深依据太原市地下管道的一般情况取为1.5m,实验管道材料选取实际给水管道PE100,即在竖直方向,该模拟实验的几何相似比约为1。在水平方向,由于实际情况的沉降区长度无法预计,在模拟实验中,根据实验场地条件选取3m的沉降区进行模拟。
2.2 确定相似影响因素
前文已经论述了实验模型和实际工程的几何相似性,但几何上相似的两个系统并不见得在物理性质上也相似,怎样使得实验模拟模型与工程实际在物理性质上保持相似性呢?因为由量纲均为1的量构成的物理方程是不存在尺度问题的,即把相应的物理方程无量纲化以后就可以适用于所有尺度,所以在物理上相似的条件是有关的量纲为1的组合量具有相同的数值,即使得两个系统的相似判据保持一致。
当管子两端拉力约束小时,管子达到破坏时的竖向变形就大,反之,管子的竖向变形就小,所以模拟管子的实际两端拉拽力很重要。在实验中,将管子的两端固定以模拟在工程实际中管子近似于无限长时对沉降区那段管道的拉拽作用。同时,在实际地下管道埋置中,管子时刻受着上部土和交通荷载的压力,以及在土体发生沉降过程中,土体施加于管道的力,在反映应力与应变关系的物理方程中涉及到材料的弹性模量和泊松比,所以管子的弹性模量E和泊松比μ应作为我们考虑实验模拟的重要因素;管子的外径D和壁厚T作为管道的本身物理特征,在土体沉降过程中影响着管道的应力和变形,应加以考虑;管子的埋深z和土的重度γ影响着管子所受的上覆土压力应加以考虑;管道下方土体的抵抗变形能力对管子在土体沉降过程中的应力和变形起着重要影响,考虑为由土体的侧限压缩模量Es反映;不论是在沉降过程中还是沉降结束以后,土体与管道之间的摩擦力对管道的受力变形均起着重要的影响作用,考虑管土之间的摩擦角φ以反映此影响。
尽管土体在沉降过程中所呈现的是一种类似于流体的状态,其主要受到重力的影响,根据流体相似理论,在此过程中,原型和模型的弗劳德数应该一致,但实际沉降的速度很难测定,所以就导致了土体沉降过程的模拟十分困难。在此种情况下,文献[9]指出在考虑不均匀沉陷对埋地管线的作用时,忽略惯性力的影响,简化为拟静力问题来考虑。这样的话,我们完全可以忽略土体的实际沉降速度,即不把沉降过程中的土体看作是流体,而只考虑已经分析得到的其他的影响因素的相似量纲分析,就可以对实际土体沉降过程做出很好的模拟。
将管线沉降破坏问题所涉及到的几个物理量进行量纲分析:
管道的弹性模量E的量纲[ML-1T-2];
管道泊松比μ的量纲[1];
管道外径D的量纲[L];
管道壁厚T的量纲[L];
管道的埋深z的量纲[L];
土体与管道的摩擦角φ量纲[1];
土体重度γ的量纲[ML-2T-2];
土体的侧限压缩模量Es的量纲[ML-1T-2].
这8个变量应该满足一定的函数关系式,将其表示如下:

除去量纲为1的两个量,对其余的量做量纲分析;


求解齐次线性方程组AX=0,因rank(A)=2,所以方程组有n-r=6-2=4个基向量,如下:

于是相似判据为:

并可以代替其来反应物理过程。
2.3 相似判据物理意义的分析
对于上述量纲分析中的齐次方程的求解,其实是可以有很多种基向量组合的,也就是说,通过以上方法可以确定出不同组合的相似判据,怎么针对具体的工程实际来选定基本影响因素,以得到合适的相似判据是需要考虑的问题。
得到的相似判据在影响因素的组成上应有其比较明确的物理意义,这样才能够了解每一个相似判据在实验模拟中所起的具体相似作用。
π1:E为管道的弹性模量,zγ表示管道上覆土体对管道的压力,故π1表征管道上覆土体对于管道弹性变形的相似模拟依据。
π2,π3:D表示管道的外径;T 表示管道的壁厚;z表示管道的埋深。这两个相似判据从实验模型的几何尺寸外形上进一步表征了模拟实验的物理相似性。
π4:Es是土体的侧限压缩模量,它在此表征发生沉降之后,管道下方土体所发生的变形情况,进而表征其对于管道的支撑能力;zγ表示上覆土对于管道的均布压力。故π4表征管道下方土体在沉降受力过程中产生变形进而影响到管道变形的相似模拟依据。
3 模拟实验的建立和数据分析
实际的地下管道上部直接填埋500mm厚的沙土,管道下部在原土地基上铺100mm厚沙土,所用沙土中水的质量分数为10%,干重度为14.2kN/m3。实验模拟中,由于采用的管道是和实际情况相同的PE100给水管,故采用与实际情况具有相同含水率的沙土作为实验用土,并压实到其干重度与实际所用沙土相近,以保证实际情况和实验模拟管土之间的摩擦角φ相似。
实验采用和实际给水管道相同的PE100管材,故管道泊松比μ一致,满足相似要求。
填埋在管道上部沙土上面的回填土为开挖出来的原土,其重度约为16.7kN/m3,厚度为1m左右。在实验模拟中采用重度相同的袋装土形式进行模拟,以保证实际情况和实验模拟满足相似判据π1=Ez-1γ-1。
相似判据π2,π3由几何相似已经满足。
管道下方的原状土地基的侧限压缩模量约为Es=4.52MPa。考虑到实验的模拟沉降方式为人工掏土,且实验管道只有1m的底部填土,如果管道下方用黏性土模拟,可能由于实验场地狭小的限制和黏性土的自身黏聚力的影响,产生不了足够大的土体沉降,而不能使得管道如真实发生沉降时那么快速剧烈地变形,因此,实验选用了流动性较大的沙土来进行模拟。通过测量模拟实验所用沙土不同干密度下所对应的侧限压缩模量,得出两者的曲线关系图。实验所用沙土在两侧墙体的约束下用振捣压实的方法控制其干密度,依据已经得到的沙土干密度和侧限压缩模量的关系曲线,使得沙土的侧限压缩模量与实际土体相近,从而保证实际情况和模拟实验遵守相似判据π4。
根据以上的相似分析,建立了如图1所示的物理实验模型。

图1 实验模型
实验模拟的是PE100给水管道的变形,并在其不同的受力部位贴应变片,以获取可靠的实验模拟数据。实验采取在管道中间底部人工掏土的方式来模拟土体的沉降,并观察记录管道的受力变形过程。
管道中间正下方的拉应变随时间的变化如图2所示。
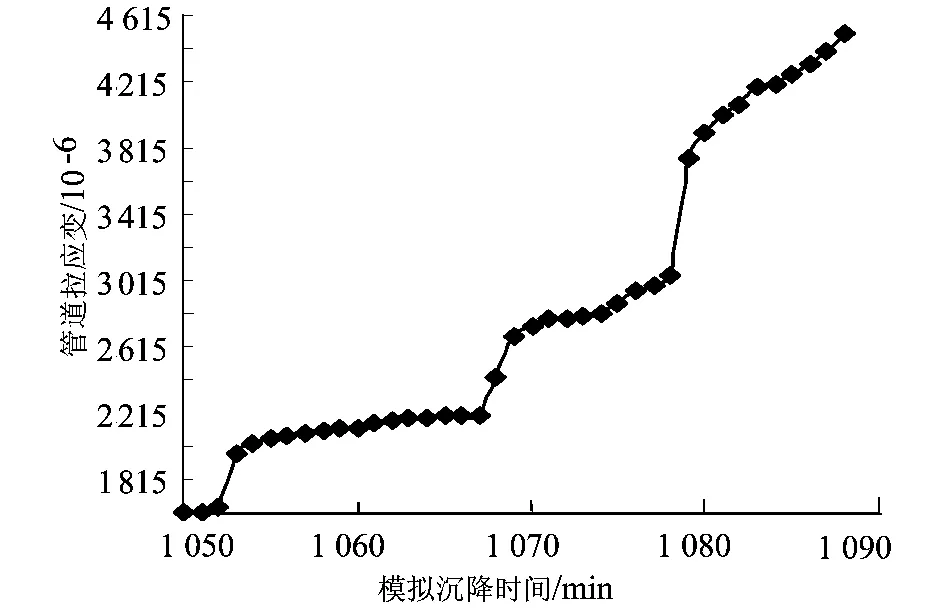
图2 管道中部拉应变与沉降时间关系曲线
管道中间正上方的压应变随时间的变化如图3所示。

图3 管道中部压应变与沉降时间关系
在人工挖土模拟沉降之前,堆积在管子上方的土体在经过了1 050min的静载以模拟实际土体的固结后,管子中间正下方产生了1 615.311×10-6的拉应变,中间正上方产生了-1524.88×10-6的压应变,所以图2,图3在反应土体沉降与时间关系的时候,时间坐标原点是从1 050min处开始的。
管道中部挠度与时间的关系如图4所示。
4 实验结果讨论
从图2和图3两组实验数据对比来看,管道的受拉和受压部位的变形能够很好地相符合,无论管道的拉应变还是压应变均随着模拟实验时间的推移而明显变大。
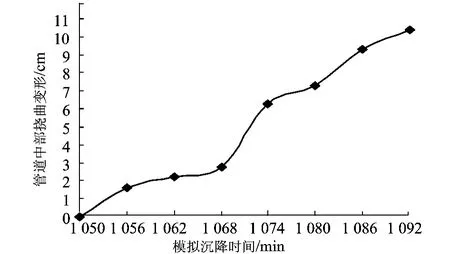
图4 管道中部挠度与沉降时间关系
由管道中部拉应变与模拟沉降时间的关系以及沉降时间与管道中部挠度的关系,并由PE100管道的弹性模量E=1.25GPa算出相应拉应变下的管道拉应力,从而得出管道中部拉应力和管道中部挠曲变形的关系曲线图如图5所示。

图5 管道中部挠度与拉应变的关系
管道中部所受拉应力随着管道中部挠曲变形的增加而明显增加,其与文献[9]纯理论计算得出的管道应力和土体沉降的关系一致。
实验模拟土体沉降,使管子弯曲,如图6所示。

图6 实验模拟土体沉降
管子取出后,其中部最终挠曲变形为22cm,如图7所示。
在模拟实验结束后,保持管道上部静载4d之后取出管子。如图7管道的中间挠度为22cm,拉应变达到10 000με,计算拉应力值为12.5MPa。同时,管子中部正下方只是出现白色受拉纹路并没有破坏,与其设计强度22MPa是符合的。

图7 管道的最终挠度
5 实验数据和工程实际数值的转换关系
由于实际发生土体沉降区域的长度不定,故模拟实验不可能准确模拟实际沉降区长度。用σ表示管道在土体沉降时所受的应力,l表示土体沉降区长度,根据文献[9]中的理论计算,当土体的沉降深度一定时,σ应该是随着l的增大而减小的。假定两者大致符合反比例函数,则在此我们将管道所受应力σ和土体沉降区长度l合在一起看作一个整体,然后对其进行量纲分析,从而找到一个σ随l变化的函数关系式,以达到相应的模拟转换效果。
建立如下的函数关系式:得到与

h(E,μ,D,T,z,γ,φ,Es,σl)=0
等价的函数表达式:
δ(π1,π2,π3,π4,μ,φ,z-1γ-1σl)=0.
通过变形得到:
Z-1γ-1σl=Ω(π1,π2,π3,π4,μ,φ),
从而得到:
σ=Zγl-1Ω(π1,π2,π3,π4,μ,φ).
模型中的物理量和工程实际中的物理量都应符合这个函数关系式:
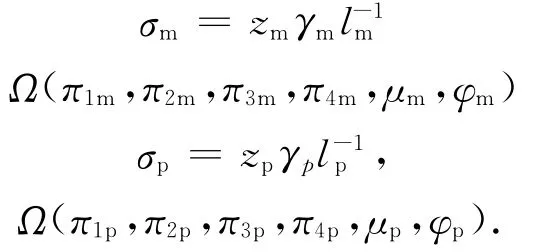
因为在物理实验模型和工程实际中,已经使得π1,π2,π3,π4,μ,φ是相等的,所以将上面的两个等式相比,得实验数值和工程实际数值的转换关系式:
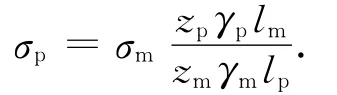
下标m表示模型实验的量,下标p表示原型实际的量。
6 结束语
1)笔者基于相似原理和量纲分析对实际土体沉降引起管线破坏的物理实验模拟进行了相似性研究,提出了对于土体沉降引起管线破坏变形这一物理过程的实验模拟所应遵守的相似判据。通过分析依据此相似判据建立起来的模拟实验的数据说明了这一相似判据的合理性,从而可以为以后相关的实验模拟研究提供参考。
2)针对室内模拟实验不可能完全相似模拟实际沉降区长度这一问题,本文根据量纲分析原理提出了基于一定沉降区长度的模拟实验来计算实际不同沉降区长度的管道受力公式,这样,我们便可以在初步观测到实际地面沉降长度时就能有效地预估其施加于管道的压力,从而采取相应的措施。
[1] 唐顺勇,李宏男.输电塔气弹模型制作及风雨荷载的相似比研究[J].振动与冲击,2011,30(8):199-202.
[2] 陈常念,韩吉田,邵莉等.气液两相流动及沸腾传热流体模化分析 [J].热科学与技术,2011,10(1):18-23.
[3] 李会知,刘敏珊,吴义章.结合工程实例讲授相似理论[J].力学与实践,2005,27:88-89.
[4] 冯建刚,成斌,王晓升.基于定理的虹吸式出水管原型和模型虹吸形成时间的相似分析[J].清华大学学报(自然科学版),2011,51(4):503-507.
[5] 胡云.基于量纲分析的建模研究[J].大学物理,2006,25(12):18-21.
[6] 李国梁,康后金,韩超.深基坑大型物理模拟实验土质相似材料的研究 [J].公路,2011,10:184-187.
[7] 范鹤,刘斌,范泽,等.高填土涵洞相似材料模型试验与数值模拟[J].吉林大学学报(工学版),2008,38(2):399-403.
[8] 易刚,龚代瑜.试论结构模型设计中的相似理论 [J].国外建材科技,2004,25(5):38-39.
[9] 高惠瑛,冯启民.场地沉陷埋地管道反应分析方法[J].地震工程与工程振动,1997,17(1):68-74.
[10] 朱庆杰,刘英利,蒋录珍,等.管土摩擦和管径对埋地管道破坏的影响分析[J].地震工程与工程振动,2006,26(3):197-199.
