亚轨道飞行器返回轨迹快速优化

王文虎

中北大学机电工程学院，太原 030051

亚轨道飞行器(Suborbital Launch Vehicle，SLV)是指从地面发射，在亚轨道空间运行作业，然后重返地面的跨大气层可重复使用飞行器[1]。SLV返回段具有飞行高度低、任务多样性、飞行环境多变的特点。

快速、准确、鲁棒的SLV返回轨迹优化可以实现快速任务规划从而极大地降低成本。返回轨迹优化本质是求解一类高度复杂的最优控制问题。常见的数值方法主要包括间接法和直接法。近年来，直接法中的伪谱法因其求解精度高、收敛速度快、具有很好的鲁棒性而备受关注[2]。伪谱法主要有：勒让德伪谱法(Legendre Pseudospectral Method, LPM)、拉道伪谱法(Radau Pseudospectral Method, RPM)和高斯伪谱法(Gauss Pseudospectral Method, GPM)。

国内外关于GPM及LPM研究较多，而RPM国内未见相关文献。Huntington[3]对上述3种伪谱法在计算效率和精度方面进行了比较，但所用的RPM是向后Radau伪谱法，并且算例较为简单，没有比较各种伪谱法在处理复杂问题时的能力。目前，国内外还没有文献对向前RPM与GPM进行过比较。

本文针对亚轨道飞行器，分别采用GPM和向前RPM进行了SLV返回轨迹快速优化研究，同时对2种伪谱法进行了比较分析。结果表明，Gauss伪谱法在处理含控制量约束的问题时比向前Radau伪谱法更具优势。

1 Gauss伪谱法与向前Radau伪谱法

1.1 Gauss伪谱法与向前Radau伪谱法基本原理

伪谱法是一种正交配点法，其基本思路为：通过选择合适的正交配点与节点，构造全局插值多项式来逼近状态和控制变量，配点处状态量的导数可由全局插值多项式求导来近似，从而将微分方程约束转换为一组代数约束。性能指标中的积分项可由相应的Gauss求积公式计算得到。经上述离散化方法，原最优控制问题转化为非线性规划问题，而后通过有效的大规模稀疏NLP求解器即可求解。

Gauss伪谱法与向前Radau伪谱法基本原理如图1所示，其主要区别在于：1)选用的配点不同。GPM选勒让德-高斯(Legendre-Gauss, LG)点∈(-1,1)，而向前RPM选标准勒让德-高斯-拉道(Legendre-Gauss-Radau, LGR)点∈[-1,1)；2)近似状态量所用的方式不同。GPM用LG点与初始时刻点为节点构造插值多项式，终端状态通过高斯求积公式得到，而向前RPM用全部离散点为节点构造插值多项式近似所有状态量。关于Gauss伪谱法文献较多，在此不再赘述。具体GPM离散化方法可参见文献[4]。

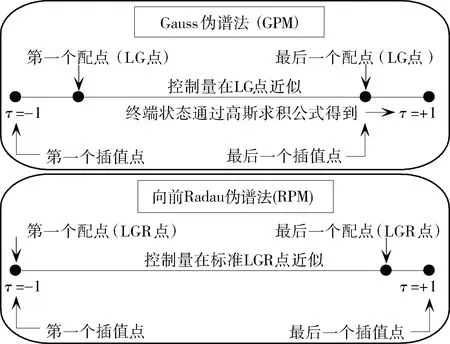
图1 Gauss伪谱法与向前Radau伪谱法基本原理图

1.2 向前Radau伪谱法离散化最优控制问题[5]

1)时域变换

为将原问题由t∈[t0,tf]转化到τ∈[-1,1]，对时间变量t作变换：

(1)

时域变换后的Bolza问题如下：

性能指标

J=Φ(x(-1),t0,x(1),tf)+

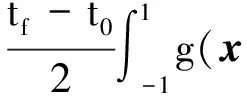
(2)

动力学微分方程约束

(τ),u(τ),τ;t0,tf)

(3)

边界条件约束

φ(x(-1),t0,x(1),tf)=0

(4)

路径约束

C(x(τ),u(τ),τ;t0,tf)≤0

(5)

2)配点选取及状态与控制变量的近似

选N次与N-1次Legendre正交多项式之和PN(τ)+PN-1(τ)的根即标准LGR点作为配点，配点数为N。以τN+1=1和N个标准LGR点为节点构造Lagrange插值多项式来近似状态变量：

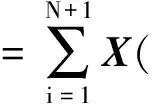
(6)

Li(τ)(i=1,…,N+1)为Lagrange基函数。

以N个LGR点为节点构造Lagrange插值多项式来近似控制变量：

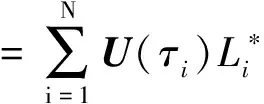
(7)

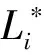
3)动力学微分方程转化

对(6)式求导，结合(3)式可以得出：

,Uk,τk;t0,tf)=0

(k=1,…,N)

(8)

其中Xk=X(τk)∈Rn，Uk=U(τk)∈Rm为配点处状态和控制量，Dki∈RN×(N+1)为微分矩阵，可通过式(9)离线确定：

(9)

其中φ(τi)=(1-τi)[PN(τi)+PN-1(τi)]。

4)性能指标

性能指标中的积分项均通过高斯拉道求积公式来近似：

J=Φ(X0,t0,Xf,tf)+

(10)

其中，wk为高斯拉道求积公式权系数。

5)边界条件约束与路径约束

边界与路径约束只需将离散状态和控制量代入式(4)，(5)即可。

至此，由式(8)，(10)以及离散化后的式(4)，(5)将原最优控制问题转化为非线性规划问题。

2 SLV返回轨迹优化

2.1 动力学模型

考虑地球旋转影响，假定飞行器侧滑角为0，SLV无动力返回动力学方程为[6]：

γ

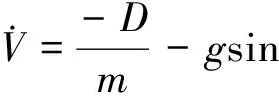
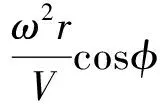
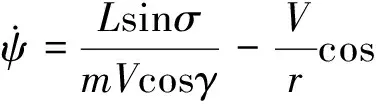
2ω(tanγcosφsinψ-sinφ)-

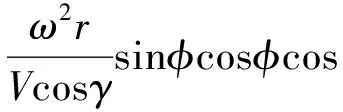
(11)

从实际系统考虑，控制舵面偏转限制必然使得攻角α、倾侧角σ存在带宽和速率限制，在模型中考虑α，σ角速率限制。令

，

(12)

由式(11)与(12)联立，可得最优控制问题状态变量X=[rθφVγψασ]T∈R8，而控制变量为U=[uαuσ]T∈R2。uα,uσ称为“伪控制量”，可以对其加以限制来满足实际控制能力约束。

为加快优化速度、有效地利用自动微分技术，密度ρ(r)、当地音速a(r)以及升阻力系数CL,CD均采用拟合模型。

当李莉把交了两个月租金的出租屋让给许峰，自己投奔梅子的时候，梅子指着她的脑袋痛心疾首：“世界上最傻的女人就是你，许峰那个白眼狼，一看就是个攀高枝的。他骗你骗得高段啊，你走得那个顺溜啊。”

2.2 优化性能指标与各类约束

1)性能指标与终端约束

为描述性能指标与终端约束，引入“末端进场走廊”(FAC)概念(见图2)，FAC也可以理解为“进场着陆窗口”，是在返回段终端速度、航迹角与航向角、着陆场位置及方向给定情况下，能够保证飞行器安全返回的终端位置(经纬高)的范围。

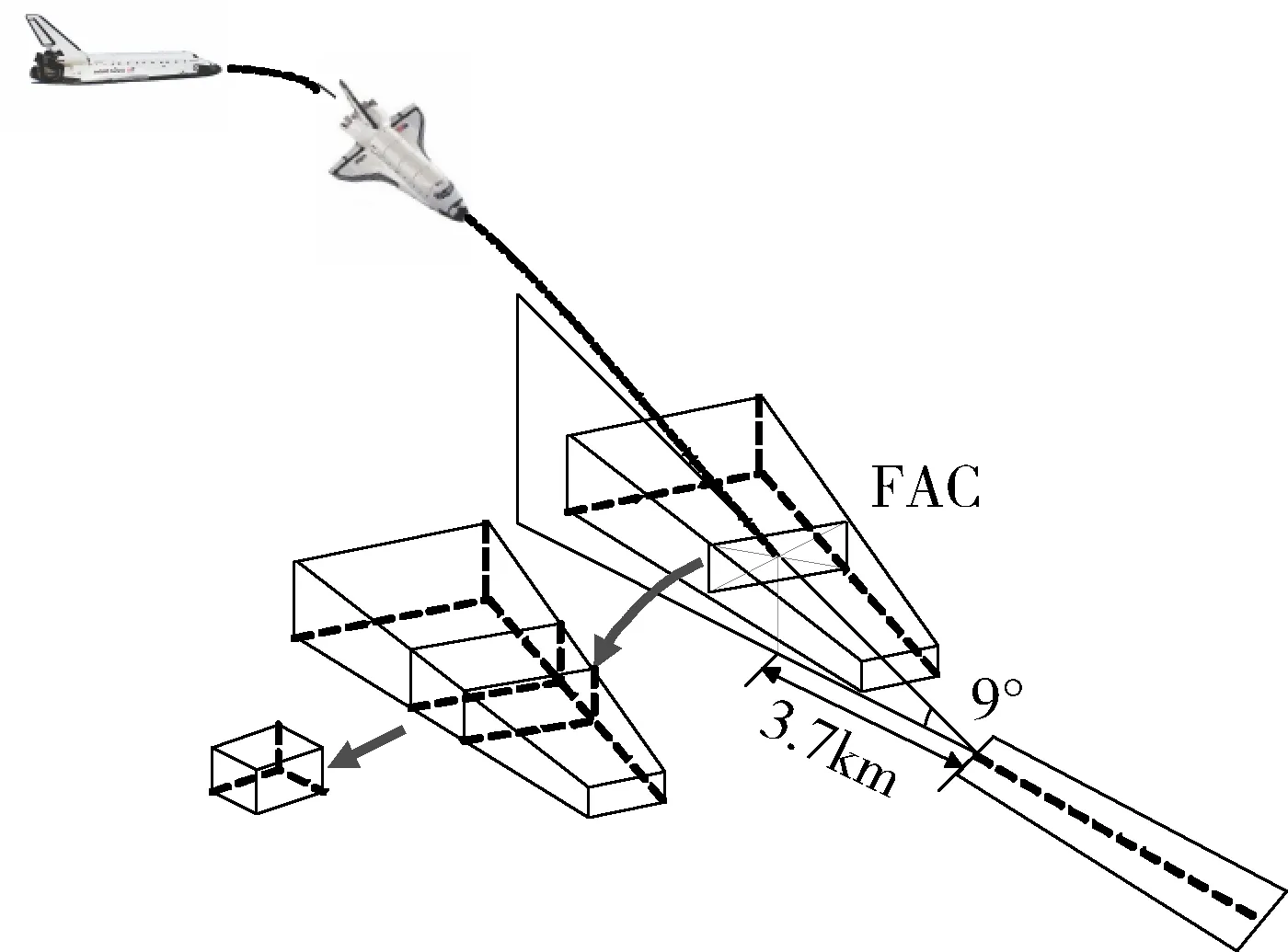
图2 末端进场走廊(FAC)[6]

终端约束要求在满足其它各类约束条件下飞行器能够准确的捕获FAC，即

≤r(tf)≤

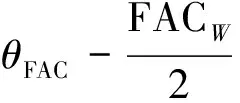
V(tf)=Vf

γ(tf)=γf

ψ(tf)=ψf

其中rFAC，θFAC，φFAC分别为FAC中心的地心距、经度、纬度，FACL，FACW，FACH分别为三维FAC的长、宽、高。

由于SLV返回的主要目标是能够安全返回指定的着陆场，因此选择如下性能指标：

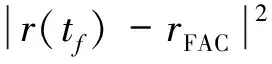
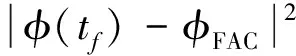
w1,2,3为权重系数，这里选w1,2,3=1，即使得终端位置与末端进场走廊中心位置距离最小。

2)其它约束

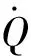
3 优化算例与结果分析

3.1 优化算例

本文采用X-33总体参数及气动模型进行仿真计算[6]。SLV质量35828kg，参考面积149.3881m2，地球半径Re取6378.1km。

返回初始状态与终端条件约束：

[r0,θ0,φ0,V0,γ0,ψ0]=[6429.1km,-85°,30°,2.6km/s,-1.3°,0°]

[Vf,γf,ψf]=[91.44m/s,-6°,-60°]

[rFAC,θFAC,φFAC]=[6378.7km,-80.7112°,30°]

[FACH/2,FACW/2,FACL/2]=[122m,0.00137°,0.001097°]

返回过程中状态量约束：

≤≤

伪控制量约束：

≤≤

过载、动压、热流等路径约束：

≤≤

3.2 优化结果

分别采用Gauss伪谱法和向前Radau伪谱法对不采用伪控制量和采用伪控制量2种情况进行了优化，采用国外大规模稀疏NLP软件包SNOPT求解，优化结果如表1及图3～7所示。两种方法均选用30个配点，优化时间都在10s以内，考虑到本文算法在Matlab平台下实现，雅克比矩阵通过自动微分方法计算，如采用C代码、解析雅克比矩阵、无量纲化动力学方程等手段，优化速度有望进一步提高。优化性能指标表明终端时刻飞行器非常接近FAC中心。由图4可以看出，采用伪控制量后GPM和向前RPM的攻角、倾侧角曲线更为平滑。图5表明采用GPM，控制量变化率均在要求的±5(°)/s范围内，而采用向前RPM倾侧角变化率在终端时刻达到了-5.21738(°)/s，超出了要求的范围，这是由于标准LGR点不包括终端时刻，导致向前RPM在处理终端控制约束时受限。图6表明返回过程满足热流、法向过载及动压等路径约束。两种方法结果趋势基本吻合，由于配点个数较少，也导致了一些差异。

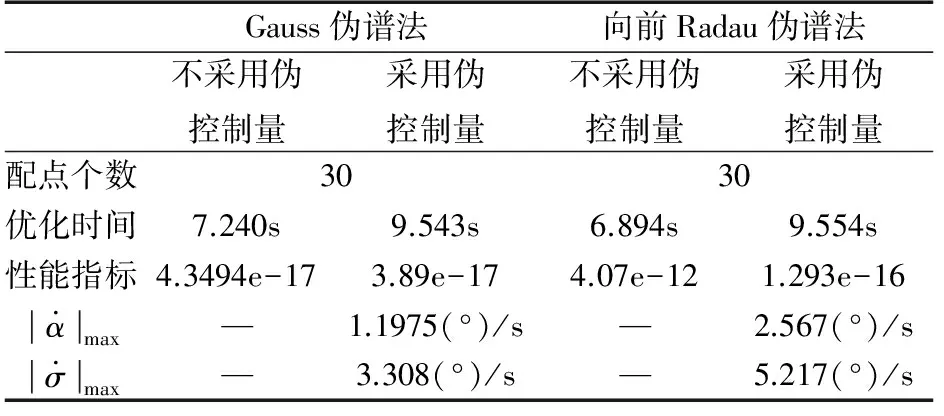
表1 优化结果比较

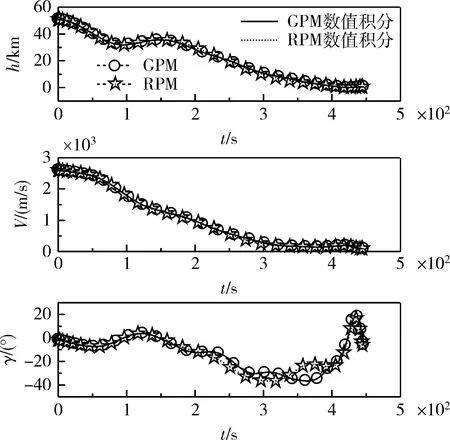
图3 状态量变化曲线

图4 控制量变化曲线

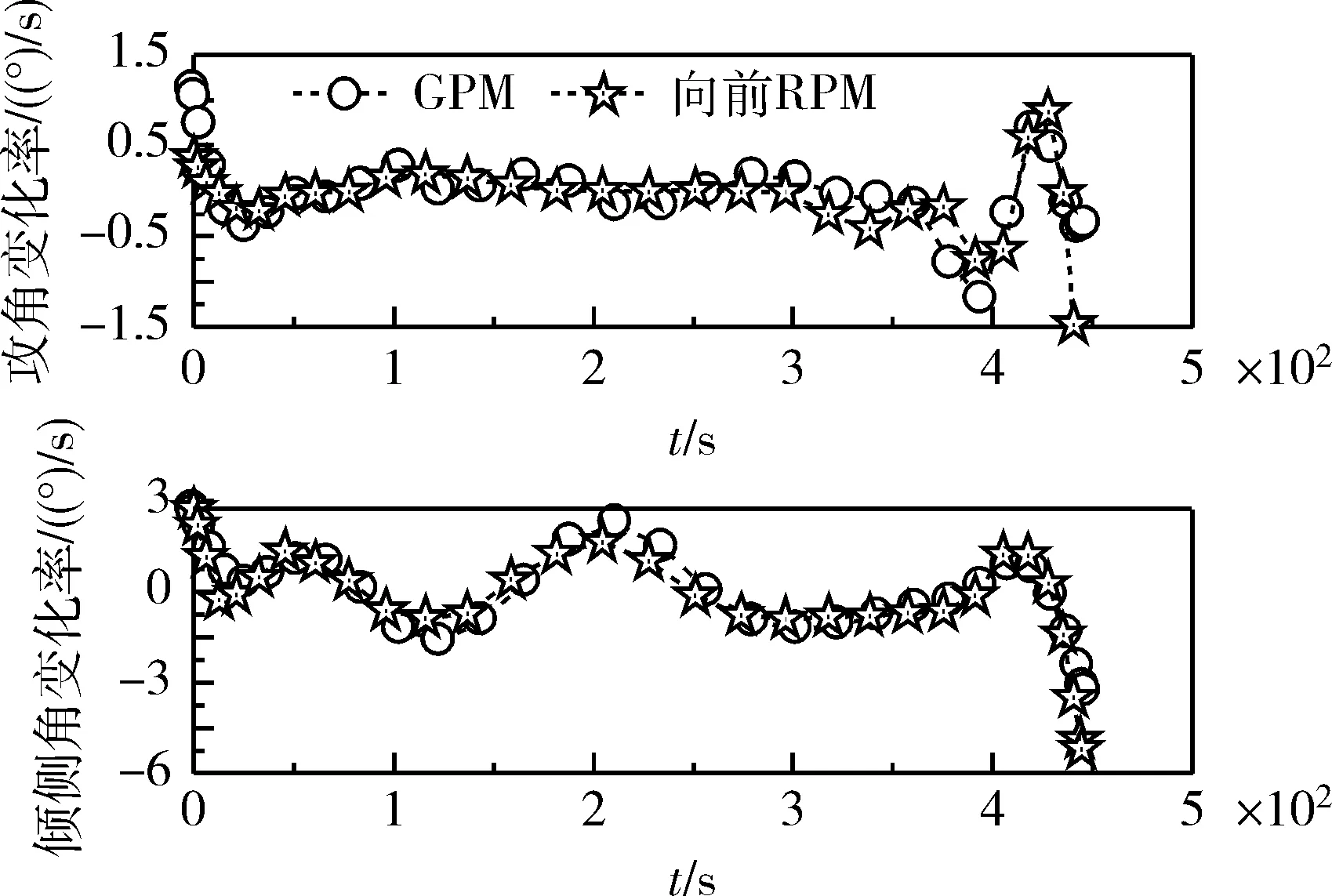
图5 伪控制量变化曲线

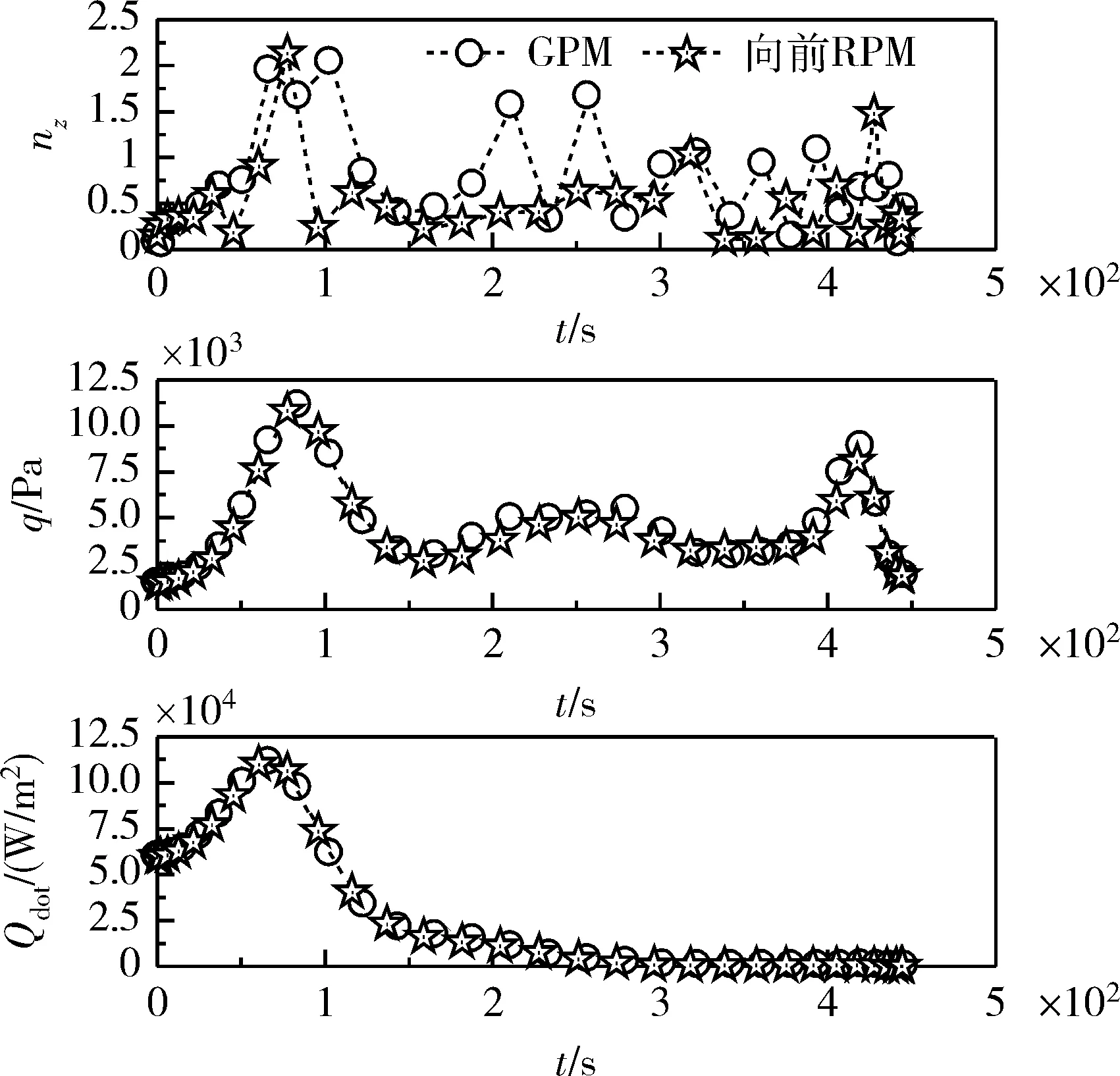
图6 路径约束变化曲线

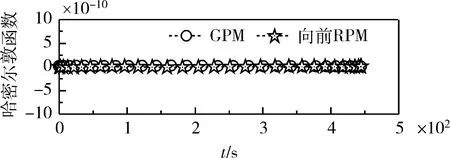
图7 哈密尔敦函数变化曲线

3.3 可行性与最优性验证

对于采用离散化方法求解连续最优控制问题而言，验证解的可行性与最优性是非常必要的。

可行性通过数值积分结果与优化结果相比较来验证，积分时的控制量由最优离散控制量插值得到。从图3中可以看出GPM及向前RPM优化与数值积分结果非常吻合，表明所得结果是可行的。

与一般直接法不同，伪谱法可以根据协态映射原理估算配点处的协态信息，从而求得哈密尔敦函数值以检验解的最优性。对于存在路径约束、终端时刻自由的自治系统最优控制问题，最优轨迹对应的哈密尔敦函数应恒为0。图7中哈密尔敦函数接近于0，实际数据在10-11量级，可以认为所得结果接近最优解。

4 结论

本文利用Gauss伪谱法和向前Radau伪谱法进行了亚轨道飞行器返回轨迹优化，比较了2种方法在处理复杂问题时的能力。仿真结果表明，在满足控制能力约束、路径约束等条件下，GPM能够快速准确地生成捕获FAC中心的SLV返回轨迹。这2种方法计算效率相当，但向前RPM在处理存在控制量约束问题时效果不佳，不能满足终端控制能力约束。

参 考 文 献

[1] Martin J C and LAW G W.Suborbital Reusable Launch Vehicles and Applicable Market[R].The Aerospace Corporation Report, 2002.

[2] Fahroo F, Ross I M.Advances in Pseudospectral Methods for Optimal Control[C].AIAA Guidance, Navigation and Control Conference and Exhibit.Honolulu, Hawaii, 2008:1-23.AIAA 2008-7309.

[3] Huntington G T, Benson D, Rao A V.A Comparison of Accuracy and Computational Efficiency of Three Pseudospectral Methods[C].AIAA Guidance, Navigation, and Control Conference and Exhibit.Hilton Head, South Carolina, 2007:1-25.AIAA 2007-6405.

[4] Huntington G T.Advancement and Analysis of a Gauss Pseudospectral Transcription for Optimal Control Problems[D].Cambridge, MA: Massachusetts Institute of technology, 2007.

[5] Garg D, Patterson M A, Darby C L, et al.Direct Trajectory Optimization and Costate Estimation of General Optimal Control Problems Using a Radau Pseudospectral Method[C].AIAA Guidance, Navigation, and Control Conference.Chicago, Illinois, 2009:1-29.AIAA 2009-5989.

[6] Singh B, Bhattacharya R.Optimal Guidance of Hypersonic Vehicles Using B-Splines and Galerkin Projection[C].AIAA Guidance, Navigation, and Control Conference and Exhibit.Honolulu, Hawaii, 2008:1-11.AIAA 2008-7263.