一种天基光学GEO目标定位方法及初轨算法观测几何评价

王雪莹 李 骏 安 玮

国防科技大学电子科学与工程学院，长沙 410073

地球静止轨道(Geostationary Orbit,GEO) 是特殊的地球同步轨道(Geosynchronous Orbit),轨道高度为35786km，轨道周期与地球自转周期(23h56m4s)相同，因而在通信、导航等领域有其独特的优势。但由于GEO上可容纳的航天器数量是有限的[1]，因而这一轨道就更显“拥挤”，而这一区域的空间碎片不但占据了宝贵的GEO 轨道资源，还严重影响了GEO卫星的安全[2]，加强对GEO附近天区(轨道高度(35786±75)km，轨道倾角±15°)空间目标尤其是碎片的监视与编目，能够有效利用GEO轨道，也可为在轨工作的航天器规避碰撞提供有效引导信息。

由于距离等约束，地基雷达对GEO目标的观测大多限于直径大于1m的目标[3]，对于尺寸较小的目标，只能通过天基平台观测，而天基观测平台因其自身工作模式等原因，单个平台在单周期之内对目标仅有数十秒到数分钟可观测时间[4]，如何有效利用短弧观测成为一个关键问题，李骏将Milani等人[5]研究太阳系小行星运动时对短弧测角数据处理方法引入天基空间目标监视信息处理中，提出了一种合理应用短弧测角数据的方法，但对新目标的短弧测角数据而言，其处理结果仍无法直接引导平台观测。

刘光明、潘晓刚等人[6-7]参照卫星导航精度衰减因子的定义[8],引入了几何精度因子(Geometric of Precision, GOP)的概念,证明了定轨精度一定程度上依赖于几何精度因子，对几种极限情况做了解释，并仿真分析了定轨精度与几何精度因子的关系，但未对多平台多测量弧段GOP做出定义与分析。

本文针对天基光学监视系统对GEO目标可观测时间较短的特点，利用标准GEO高度作为约束条件，以短弧观测内GEO目标做匀速运动为基本假设，解算观测平台位置、观测角度与距地高度为35786km的空间球面构成的方程，取合理解作为空间目标的位置，再用最小二乘法拟合出目标的位置、速度，以此为初始值利用J2的摄动模型外推，预报目标轨道，引导天基平台，对目标进行后续观测。并用广义Laplace算法[9-10]对多段观测弧段处理，得到有效初轨，为评价多弧段观测数据定轨的观测几何，提出一种修正的几何精度因子(Geometric of Precision, GOP)概念，为描述测量误差对定轨结果的影响程度，提出几何精度因子的误差灵敏度(Error Sensitivity Geometric of Precision, ESGOP)概念。

仿真结果表明短弧测量条件下，利用约束条件求出的目标位置、速度可以有效引导短期内对目标的观测，也可作为初轨算法的初值输入，GOP可用来表征系统的可观测特性，ESGOP可以反映观测条件对测量误差的灵敏程度，GOP和ESGOP从本质上反映了观测几何与定轨精度的关系。

1 天基光学观测模型

1.1 观测几何关系

在J2000.0地心惯性坐标系下，设地心原点为O，R为测站Δt的位置矢量，r为目标S的位置矢量，而ρ为S相对测站的观测矢量，如下图所示。

图1 观测几何关系

则有r=ρ+R

(1)

其中测站矢量R已知，观测矢量ρ=ρL，L为单位观测矢量，由目标赤经α和赤纬δ确定

(2)

1.2 测量模型

赤经α和赤纬δ由J2000.0坐标系下目标位置矢量r=(x,y,z)和测站位置矢量R=(X,Y,Z)确定

(3)

2 几何约束下的GEO目标定位

,j=1,…,M

平台的位置矢量为Rj=(Xj,Yj,Zj),j=1,…,M。

在单个天基光学平台短弧观测中，GEO目标近似做匀速直线运动，像在平面上的轨迹一般近似直线[4]，通过在视场内标定标准同步轨道目标轨迹的方式，可迅速判断出同步带目标。

构造如下变量：

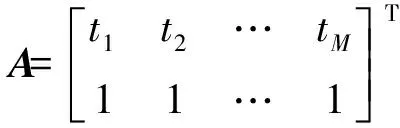
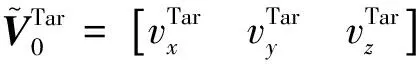
由最小二乘法的原理，可知

(4)

其中，R表示位置误差的协方差矩阵，PX0表示估计误差的协方差。

3 广义Laplace初轨算法可观测性分析

利用文献[7-8]中算法对多段观测数据处理，采用消元后的基本方程组

，(j=1,2,3,…，M)

(5)

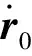
(6)

上式表示线性化后系数矩阵的子块。

对于完整的广义Laplace方程而言，表征其可观测性的法方程系数矩阵很难给出解析的表达式[11]，只能在一定假设条件下通过近似解释一些现象，为了定量描述系统可观测性，在前述的观测模型和测量集的基础上，定义2个变量。

1)几何精度因子(Geometric of Precision, GOP)：多平台(或单平台)对空间目标多个弧段的观测数据中，任取三次角度观测，观测平台指向空间目标的单位视线矢量所构成的四面体体积可用角度测量表示，遍历所有的三次角度测量组合，取所有四面体体积的最大值为几何精度因子，其表征的是某种特定观测几何下的系统可观测性。

2)几何精度因子的误差灵敏度(Error Sensitivity Geometric of Precision, ESGOP)：由实际测角信息计算的几何精度因子与平滑处理后的测角值[12-13](或理论测角值)计算的几何精度因子的相对误差。在特定的观测几何下，误差灵敏度越小，测量误差对定轨结果的影响越小。

|H|=2a2/3×Mm×Mn×Mk×GOPm,n,k×

vm×vn×vk

(7)

其中a为目标轨道半长轴，ΔE为偏近点角变化量，

·r0·ΔEk-cosΔEm)-

a·sin(ΔEk-ΔEm)-(a-r0)(sinΔEk-sinΔEm)

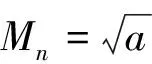
a·sin(ΔEn-ΔEk)-(a-r0)(sinΔEk-sinΔEn)

从定义可得

不难看出其可作为衡量系统可观测性的一项指标。若将平滑处理后的测角值(或理论测角值)计算的几何精度因子记为GOPopt，则有

×100%

4 仿真结果与分析

为仿真验证本文算法可获取目标有效初轨，并验证GOP和ESGOP可有效表征初轨算法性能，设置如表1所示的仿真场景。

表1 仿真参数

仿真过程中相机主要采用恒星跟踪模式[14-15]，针对几何约束下的GEO目标定位算法和广义Laplace初轨算法可观测性做如下仿真。

4.1 仿真一

观测星1的相机，在某次任务中，发现了GEO区的新目标，以1s每点的频率输出200个角度测量值，测角误差为100微弧度。利用(4)式估计初始时刻目标的位置与速度，再利用J2摄动模型外推2h的轨道与真实轨道对比，得到如图2所示结果。

从仿真结果可以看出，利用本文算法处理200s的观测数据，可有效估计出目标在参考时刻的位置速度，此值可以用作初轨算法的输入，利用估计值预测目标轨道，在1h内位置误差不超过80km，可有效引导其它平台对目标进行观测。

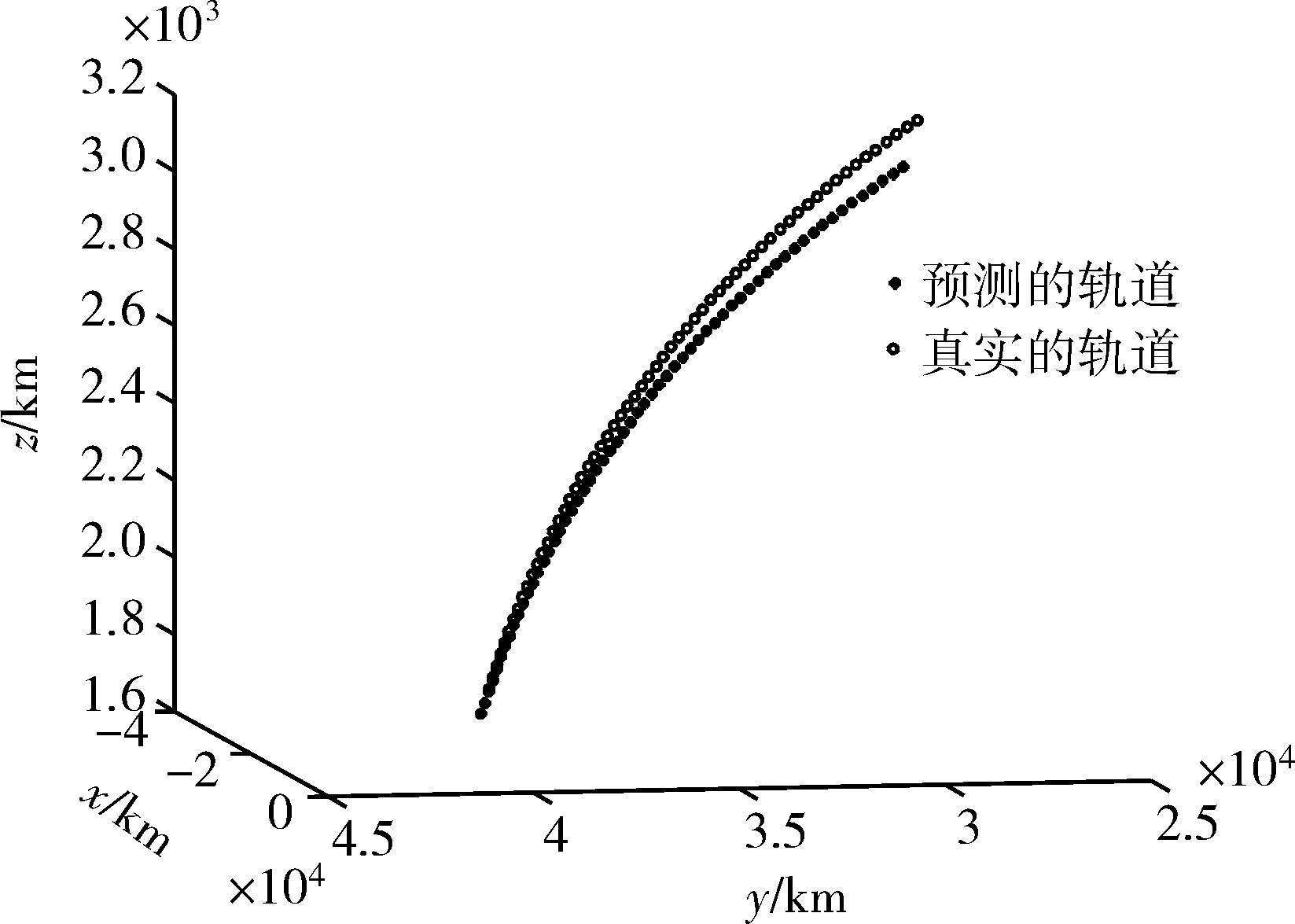
图2 预测轨道

4.2 仿真二

在可观测的弧段起始处与结束处均安排平台1对目标进行2次100s的观测，得到的数据称为单平台数据；在可观测的弧段起始处与结束处分别安排平台1和平台2对目标进行2次100s的观测，得到的数据称为多平台数据(可观测弧段不足100s时，以可观测弧段长度为观测弧长)。100微弧度测角误差下，两组数据对比得到如图3仿真结果。

从图3的仿真结果可看出，在观测弧段较短的情况下(Δt小于500s)，多平台观测的GOP及ESGOP明显优于单平台观测，因而其定位精度更高，但是随着可观测弧段增长，这种优势也渐渐变弱。这主要是由于多平台观测的优势集中体现在其良好的观测几何中，如果单平台有足够长的观测弧段，其观测几何也比较好，因而其定轨性能也会提升，亦即使用多平台多观测弧段对GEO目标定轨，可将空间优势转换为观测弧长优势。

5 结束语

本文提出一种利用天基光学短弧观测对GEO区目标定位的方法，在GEO区半径、偏心率等约束条件下，仅使用数百秒观测即可估计出目标的位置与速度，此结果可以用作初轨算法的初始值，也可以其为初值进行轨道预测，数小时内预测结果可有效引导其它平台对目标观测。为表征观测几何对广义Laplace初轨算法定轨性能的影响，将几何精度因子(GOP)的概念扩展至多平台多观测弧段，并引入几何精度因子的误差灵敏度(ESGOP)表征测量误差对观测几何的影响，仿真结果表明：对GEO目标而言，当GOP不小于0.03、ESGOP不大于0.005时，对目标的初轨精度可以控制在50km之内。

图3 不同观测弧长下单平台与多平台数据定轨性能比较

参 考 文 献

[1] 李恒年, 高益军, 余培军, 等.地球静止轨道共位控制策略研究[J] .宇航学报, 2009,30 (3) : 967-973.(LI Heng-nian,GAO Yi-jun, YU Pei-jun, et al.The Strategies and Algorithms Study for Multi-GEO Satellites Collocation [J].Journal of Astronautics,2009, 30(3): 967-973.)

[2] 梁斌, 徐文福, 李成, 等.地球静止轨道在轨服务技术研究现状与发展趋势[J].宇航学报,2010,31(1):1-13.(LIANG Bin, XU Wen-fu, LI Cheng, et al.The Status and Prospect of Orbital Servicing in the Geostationary Orbit[J].Journal of Astronautics, 2010,31(1):1-13.)

[3] 唐轶峻, 姜晓军, 魏建彦, 等.高轨空间碎片光电观测技术综述[J].宇航学报, 2008, 29 (4) : 1094-1098.(TANG Yi-jun,JIANG Xiao-jun, WEI Jian-yan, et al .Review of Optical Observations of High Apogee Space Debris[J].Journal of Astronautics, 2008,29 (4):1094-1098.)

[4] 李骏，安玮，周一宇.天基光学短弧初轨的约束微分修正方法[J].宇航学报,2009,30(2):669-774.(Li Jun, AN Wei, ZHOU Yi-yu. Constrained Differential Correction in Initial Orbit Determination with Short-arcs in Optical Space-based Space Surveillance[J].Journal of Astronautics, 2009,30 (2) :669-774.)

[5] A.Milani and G.Gronchi .Theory of Orbit Determination[M].Cambridge: Cambridge University Press,2010.

[6] 潘晓刚.空间目标定轨的模型与参数估计方法研究及应用[D].长沙: 国防科技大学, 2009.(Pan Xiao-gang.Research on Space Target Orbit Determination Model and Paraments Estimation Algorithms[D].Changsha: National University of Defense Technology, 2009.)

[7] 刘光明.基于天基测角信息的空间非合作目标跟踪算法及相关技术研究[D].长沙: 国防科技大学, 2011.(Liu Guangming.Research on non-cooperative Target Tracking Algorithms and Related Technologies Using Space-based Bearings-only Measurements [D].Changsha: National University of Defense Technology, 2011.)

[8] Cai Z W.Research on Autonomous Orbit Determination of Navigation Satellite Based on Crosslink Range and Orientation Parameters Constraining[J].Geo-spatial Information of Science, 2006, 9(1):18-23.

[9] 刘林.航天器轨道理论[M].北京:国防工业出版社, 2000.

[10] 刘林.关于初轨计算[J].飞行器测控学报，2004, 23(3): 41-50.(Liu Lin.On Initial Orbit Determination[J].Journal of Spacecraft TT&C Technology,2004, 23(3): 41-50.)

[11] 李骏.空间目标天基光学监视跟踪关键技术研究[D].长沙: 国防科技大学, 2009.(Li Jun.Research on Technologies of Space Objects Surveillance and Tracking in Space-based Optical Surveillance [D].Changsha: National University of Defense Technology, 2009.)

[12] 张玉祥.人造卫星测轨方法[M].北京:国防工业出版社, 2007.

[13] M.Ju.Sokolaskaya.On the Laplacian Orbit Determination of Asteroids[J].Planet.Space Sci., 1998, 45(12): 1575-1580.

[14] Grant H, Stokes, Curt von Braun, et al.Space-based Visible Program[J].Lincoln Laboratory Journal,1998,11(2):205-229.

[15] Jayant Sharma, Grant H, Stokes, et al.Toward Operational Space-based Space Surveillance[J].Lincoln Laboratory Journal,2002,13 (2):309-334.