合成孔径雷达子孔径数据改进ECS成像算法

杨立波 陆和平 高 磊

北京航天自动控制研究所，北京 100854

合成孔径雷达(Synthetic Aperture Radar, SAR)具有全天时、全天候，远距离、高分辨率成像等特点，并具有测距测速能力，可大大提高战场感知能力，弹载SAR已成为微波成像和精确制导领域的研究热点[1-2]。由于弹上条件限制，弹载合成孔径雷达天线孔径小，方位理论分辨率高，远大于实际需求，另外，导弹运动变化剧烈，采用子孔径数据成像，可在满足方位分辨率的前提下，减小数据采集时间和成像延时，降低处理难度和负担，是弹载合成孔径雷达一种有效的成像方式。

SPECAN(Spectral Analysis)及改进SPECAN算法[3-4]和ECS[5](Extended Chirp Scaling)算法是常用的子孔径成像算法。SPECAN算法成像效率高，易于硬件实现[6]，但这一算法仅校正距离徙动的公共线性部分，成像精度低，多用于中低分辨率成像。ECS算法是子孔径数据成像的精确算法，在弹载SAR成像中采用的较多[7-9]，该算法能进行精确的距离徙动校正和高次相位补偿，但方位向chirp scaling操作会产生大量补零问题。

本文分析了ECS算法的大量补零问题，提出一种改进ECS算法，克服了ECS需要补零的不足，并进行了仿真实验。

1 回波信号模型

弹载SAR子孔径成像几何关系如图 1所示。设雷达沿y轴方向运动，速度大小为v，斜视角为θc，点目标B的视线距离为Rc。在慢时间零时刻，雷达位于A点，波束中心穿过P点，点目标B与P点的方位距离为yn。

图1 弹载SAR子孔径成像几何关系

经过ta后，雷达位于C处，点目标B的瞬时斜距BC可表示为：

R(ta;Rc,yn)=

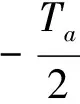
(1)

设SAR发射线性调频信号，相干接收后，点目标B的基带回波信号为：

s(tr,ta)=rect(ta/Ta)wr(tr-2R(ta;Rc,yn)/c)

wa(ta-yn/v)exp{jπkr(tr-2R(ta;

Rc,yn)/c)2-j4πR(ta;Rc,yn)/λ}

(2)

其中，c为光速，tr为距离向时间，kr，λ为发射信号的调频斜率和波长，Ta为子孔径积累时间，wr(tr)为发射信号包络，wa(ta)为方位包络，rect(ta)为单位矩形窗函数。

2 ECS算法及其补零问题

2.1 算法流程

ECS算法通过距离向Chirp Scaling和二维频域处理校正距离徙动，通过方位Chirp Scaling将方位向信号补偿为线性调频信号，并使各距离单元的调频斜率一致，解决方位向输出间隔随距离变化的问题。ECS算法流程如图 2所示。

图2 ECS算法流程

1)方位向FFT及距离向Chirp Scaling

对回波信号进行方位FFT，忽略天线方向图的加权作用，变换后的信号表达式为：

S1(tr,fa)=wr(tr-2R(fa)/c)Wa(fa)

exp{jπkm(tr-2R(fa)/c)2}

exp{-j4πRccosθcD(fa)/λ}

exp{-j2πfa(yn+Rcsinθc)/v}

(3)

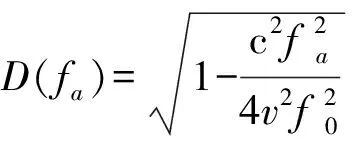
设CS操作的参考距离为Rref, r，参考频率为fref，则Chirp Scaling之后的信号为：

S2(tr,fa)=wr(tr-2R(fa)/c)Wa(fa)

exp{jπkm(tr-2R(fa)/c)2}

exp{-j4πRccosθcD(fa)/λ}

exp{-2πfa(yn+Rcsinθc)/v}

exp{jπkm(D(fref)/D(fa)-1)

(tr-2Rref,rcosθc/c/D(fa))2}

(4)

2)距离向FFT及距离压缩，二次距离压缩和距离徙动校正

距离向FFT之后的信号为：

S3(fr,fa)=wr(fr/kr)Wa(fa)

(5)

实现距离徙动校正，距离压缩和二次距离压缩的参考函数H2为：

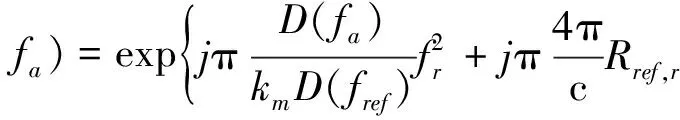
(6)

经过上述处理后的信号为：

(7)

3)距离向IFFT及相位校正

距离向IFFT后的信号表达式为：

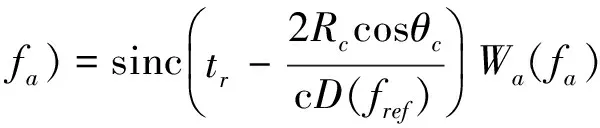
(8)

(8)式中的第3个指数项是由距离向Chirp Scaling所产生的无用相位，校正该相位的因子为

H3(Rc,fa)=

(9)

校正后的信号为

S6(tr,fa)=sinc(tr-2Rccosθc/c/D(fref))Wa(fa)

exp{-2jπfa(yn+Rcsinθc)/v}

exp{-j4πRccosθcD(fa)/λ}

(10)

4)方位向Chirp Scaling

方位向Chirp Scaling补偿方位高次相位，并调整方位调频斜率，使方位向输出间隔一致。

将D(fa)在fa=fc处泰勒展开，有：

(11)

其中，e表示高次项误差，由(11)式可得：

(12)

因此，补偿高次项相位误差的相位因子为：

φ1=exp{j4πRccosθce/λ}

(13)

为了保证方位向输出间隔一致，乘以以下频域线性调频信号：

φ2=exp{-jπλ(Rc-Rref,a)(fa-fc)2/(2v2cos2θc)}

(14)

其中，Rref, a为方位CS参考距离。

将φ1，φ2合并，可得方位向Chirp Scaling相位因子：

H4(Rc,fa)=exp{j4πRccosθc(D(fa)-cosθc)/λ}

exp{j2πRcsinθc(fa-fc)/v}

exp{jπλRref,a(fa-fc)2/(2v2cos2θc)}

(15)

处理后的信号为

S7(tr,fa)=sinc[B(tr-2Rccosθc/c/D(fref))]

Wa(fa)exp{-j4πRc/λ}

exp{-j2πynfa/v+jπλRref,a(fa-fc)2/(2v2cos2θc)}

(16)

5)方位IFFT及方位去斜和斜视校正

方位IFFT后的信号为：

(17)

其中，β=Rref,a/Rc，kref=2v2cos2θc/λ/Rref,a。

方位去斜(Dechirp)用以补偿(17)式的二次相位项，这里，我们在去斜的同时补偿多普勒中心频率，去斜函数为：

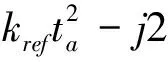
(18)

去斜成像后，yn相同的目标在图像中处于同一方位线，图像的两个方向不正交。为了使方位相同的目标在图像中处于同一方位线，可在去斜的同时乘以以下相位因子(本文称为斜视校正因子)：

H6(ta)=exp{j2πkrefRcsinθcta/v}

(19)

6)方位FFT

最后进行方位向傅里叶变换，可得成像结果：

exp{-j2π(1-β)ynfa/v}sinc[B(tr-2Rc/c)]

sinc[βTa(fa-krefya/v)]

(20)

其中，

ya=yn+Rcsinθc

(21)

为目标的方位坐标。

2.2 补零问题

由(17)式可知，经过方位向调频斜率调整，信号变换到方位时域后，一方面信号时宽发生变化;另一方面，信号出现时延。信号展宽程度与目标距离有关，信号时延大小与目标的距离和方位都有关。这种不一致的展宽和时延导致方位向信号能量分布在一个比Ta大得多的范围内。

在距离R=Rref,a+ΔR处，方位IFFT后，信号总的持续时间

(22)

信号能量分布在方位向的展宽要求ECS算法在一步处理前对信号补零，否则，方位向IFFT之后，Ta范围之外的信号能量就会卷绕进Ta内，导致最终成像结果中目标峰值降低，主瓣展宽，并出现严重的虚假目标，而方位向补零导致算法效率降低，实时性变差。

3 改进ECS算法

方位向调频斜率的一致化调整是出现上述问题的根本原因，本文算法在补偿方位向高次相位时不进行调频斜率调整，采用变标傅里叶变换(Scaled Fourier Transform, SCFT)校正方位向输出间隔随距离变化的扇形畸变。算法流程如图 3所示。

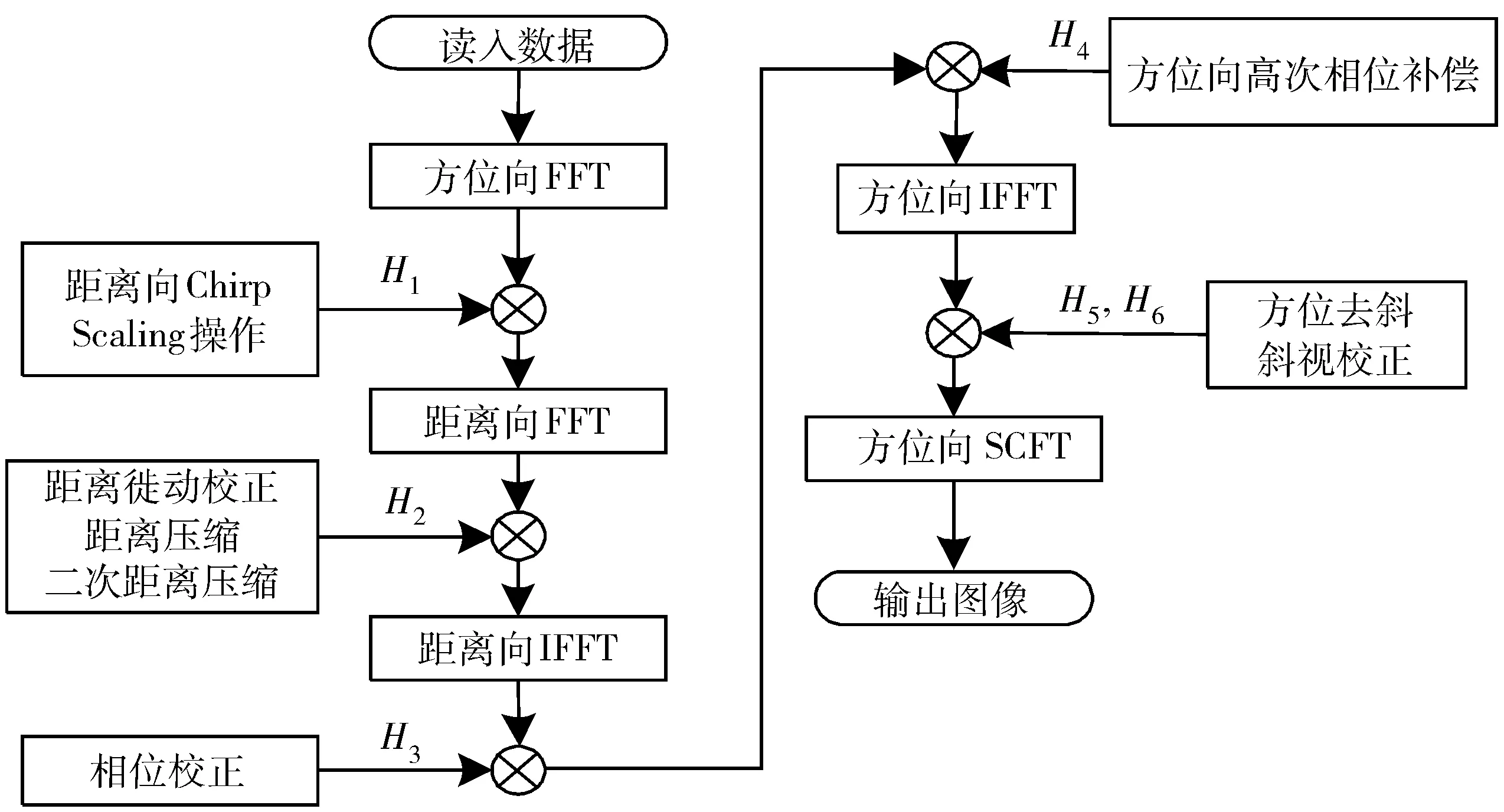
图3 改进ECS算法成像流程

方位向高次相位补偿之前的处理流程与ECS算法相同，不进行调频斜率一致化调整的方位向高次相位补偿信号H4为：

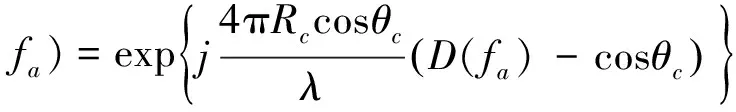
(23)

方位IFFT之后的信号为：

(24)

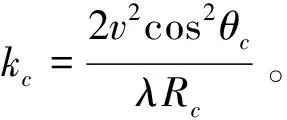
方位去斜参考信号H5变为：

(25)

斜视校正相位因子H6变为：

H6(ta)=exp{j2πkcRcsinθcta/v}

(26)

方位SCFT变换的表达式为：

S8(tr,fa)=SCFT[S7(tr,ta)]

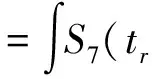
(27)

其中，α为变标因子。

SCFT可由chirp-z变换高效实现[10]，chirp-z变换将上述积分转化成卷积：

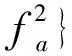
(28)

其中，S7(tr,fa)即为S7(tr,ta)，只是以变量fa代替了变量ta。式(28)中的卷积可由FFT来实现。通过FFT实现chirp-z变换的流程如图 4所示。

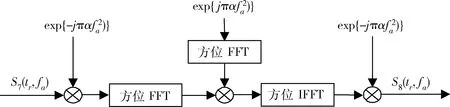
图4 FFT实现chirp-z变换流程

方位向SCFT后，可得成像结果：

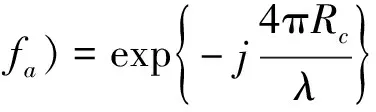
(29)

令

(30)

则(29)式为

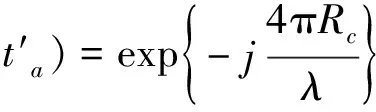
(31)

4 仿真实验及结果分析

仿真参数如表 1所示。

设置地面上大小为200m (x向)×400m (y向)的目标点阵进行仿真成像，点阵中心的斜距为9km，方位为-100m。成像结果如图 5(a)所示。为说明ECS算法在不补零情况下的目标卷绕问题，在相同条件下，采用ECS算法成像，结果如图 5(b)所示。

表1 仿真参数

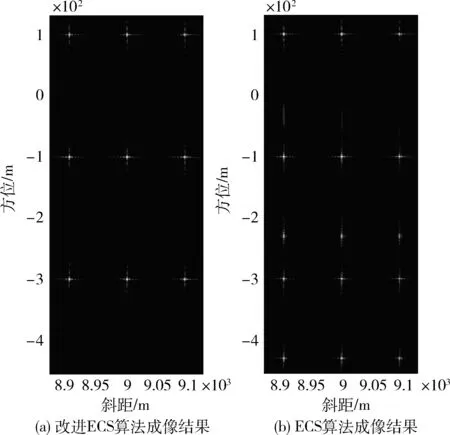
图5 改进ECS算法与ECS成像结果

由图 5可见，改进ECS算法能将目标压缩到正确位置，而ECS算法出现严重的虚假目标。

斜距为9km的3个点目标方位向性能指标如表 2所示。

表2 改进ECS(IECS)算法与ECS算法性能比较(未加权)

由表 2可见，对于改进ECS算法，3个点目标压缩性能一致，对于ECS算法，目标1和目标2产生了虚假目标，其峰值降低，主瓣展宽。

由以上仿真结果可看出，改进ECS算法可得到良好的成像结果，并能克服ECS算法中调频斜率一致化调整所导致的大量补零问题。

5 结束语

ECS算法是弹载SAR子孔径成像常采用的算法。本文分析了ECS算法方位向CS操作所产生的大量补零问题，提出了一种改进ECS算法，采用变标傅里叶变换校正方位向输出间隔随距离变化的扇形畸变，克服了ECS算法需要大量补零的不足。仿真实验表明，改进ECS算法无需补零，并可得到良好的成像结果。

参 考 文 献

[1] 尹德成.弹载合成孔径雷达制导技术发展综述[J].现代雷达, 2009, 31(11): 20-24.(YIN De-cheng.Review of Development of Missile-borne SAR Guidance Technology[J].Modern Radar，2009, 31(11): 20-24.)

[2] 秦玉亮, 王建涛, 王宏强, 等.弹载合成孔径雷达技术研究综述[J].信号处理, 2009, 25(4): 630-635.(QIN Yu-liang, WANG Jian-tao, WANG Hong-qiang, et al.Overview on Missile-borne Synthetic Aperture Radar[J].Signal Prcossing, 2009, 25(4): 630-635.)

[3] M.Sack, M.R.Ito, I.G.Cumming.Application of Efficient Linear FM Matched Filtering Algorithms to SAR Processing[J].IEEE Proceedings-F, 1985, 132(1):45-57.

[4] R.Lanari, S.Hensley, P.Rosen.Chirp-Z Transform Based SPECAN Approach for Phase-preserving ScanSAR Image Generation[J].IEE Proceedings Radar, Sonar and Navigation，1998, 145(5): 254-261.

[5] Alberto Moreira, Josef Mittermayer, Rolf Scheiber.Extended Chirp Scaling Algorithm for Air- and Spaceborne SAR Data Processing in Stripmap and ScanSAR Imaging Modes[J].IEEE Transaction on Geoscience and Remote Sensing,1996, 34(5): 1123-1136.

[6] 周宝亮, 张顺生, 戴春杨, 等.基于SPECAN技术的子孔径RD成像算法[J].通信技术,2010, 43(8): 250-252.(ZHOU Bao-liang, ZHANG Shun-sheng, DAI Chun-yang, et al.Sub-aperture RD Imaging Algorithm Based on SPECAN Technology[J].Communications Technology, 2010, 43(8): 250-252.)

[7] 刘高高, 张林让, 刘昕, 等.一种曲线轨迹下的大场景前斜视成像算法[J].电子与信息学报,2011, 33(3): 628-633.(LIU Gao-gao, ZHANG Lin-rang, LIU Xin, et al.Missile-Borne Large Region Squint SAR Algorithm Based on a Curve Trajectory[J].Journal of Electronics & Information Technology, 2011, 33(3): 628-633.)

[8] 孙兵，周荫清，陈杰，等.基于恒加速度模型的斜视SAR成像CA-ECS算法[J].电子学报, 2006, 34(9): 1595-1599.(SUN Bing, ZHOU Yin-Qing, CHEN Jie, et al.CA-ECS Algorithm for Squinted SAR Imaging Based on Constant Acceleration Model[J].Acta Electron Sinica, 2006, 34(9): 1595-1599.)

[9] ZHOU Qiang, QU Changwen, SU Feng, et al.A New Approach of Extended Chirp Scaling Algorithm for High Squint Missile-Borne SAR Data Processing[C].2008 International Symposium on Computer Science and Computational Technology, Shanghai, China, 2008: 133-136.

[10] L.R.Rabiner, R.W.Schafer, C.M Rader.The Chirp-Z Transform and Its Application[J].Bell System Tech.J., 1968, 48: 1249-1292.