质量矩控制飞行器的压心不确定性问题研究*

魏鹏鑫 高长生 荆武兴

1．哈尔滨工业大学航天工程系，哈尔滨 150001

质量矩控制技术是依靠调整质心指向压心的力臂实现飞行器机动飞行的。与传统的控制方法 (如气动舵等)相比，质量矩控制技术具有气动布局简单、无舵面烧蚀等优点，因此在大气层内高超声速飞行控制领域具有广阔的应用前景。

在弹头机动方面，俄罗斯已经实现了工程应用，美国也开展了多年研究，主要集中在Naval Surface Warfare Center和加州大学Optimal Synthesis Inc[1-3]等科研院校。国外虽然已进入工程实践阶段，但有价值的资料很难获得。国内主要在导弹总体布局方案、动力学分析和控制律设计等方面进行质量矩研究。廖国斌[4]对影响导弹快速响应的主要因素在不同条件下进行了研究，并对动力学方程进行了简化；李瑞康[5]对质量矩飞行器控制性能进行了分析；周韬[6]分析了活动质量体运动规律对导弹三通道姿态响应的影响；周凤岐[7]利用小扰动方法对弹道式导弹弹头的质量矩控制机理进行了分析；张晓宇[8]、秦莉[9]、孙卫华[10]等人在飞行器姿态控制律设计方面做了一些研究工作。

在质量矩控制中，如何提高活动质量块对系统的控制能力是研究该技术的关键。但是，由于存在着一系列与飞行器气动、结构布局密切相关的难点问题，使得对系统的控制性能研究变得很难。压心不确定性是实施质量矩控制技术的难点问题之一。压心的计算误差或风洞吹风误差在亚音速和超音速飞行中，约为全弹长度的1%～2%，在跨音速飞行中，压力中心的位置变化较剧烈，不适合采用质量矩控制。通过理论计算或风洞试验获得的标称压心点(图1中c点)与导弹实际飞行中的实际压心点存在偏差，而在有限的弹体空间内，活动质量块引起的系统质心变化范围不大，若压心偏差范围超过了系统质心的活动范围，则无法判断控制力臂的改变是来自于活动质量块运动还是压心偏差，这样无法形成正确的控制指令。

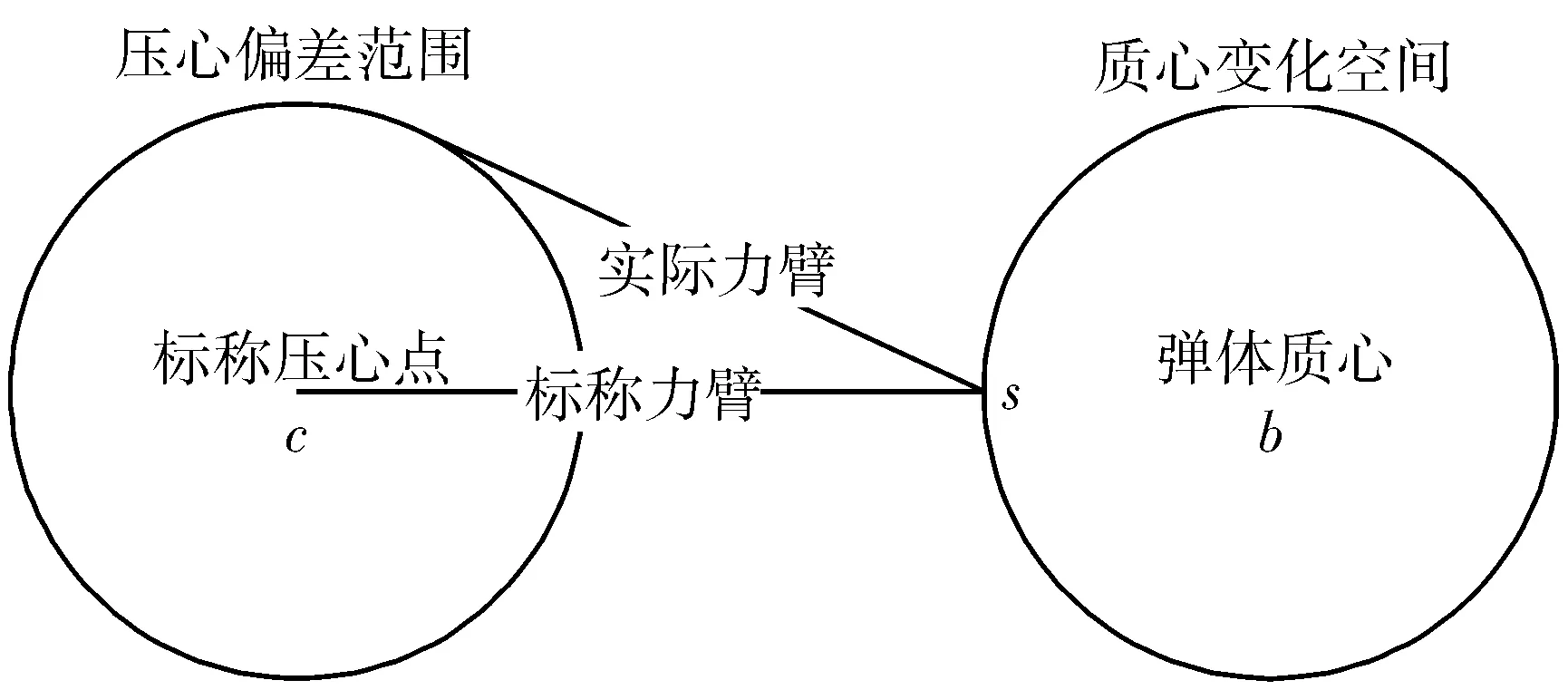
图1 压心偏差对力臂的影响示意图

本文推导了导弹姿态角与压心偏差的关系，分析了压心偏差对飞行器控制性能的影响，给出了压心最大容许偏差范围的解析解，然后针对压心偏差对飞行器的影响进行了仿真计算，并在此基础上提出了几种减小压心不确定性对飞行器控制性能影响的结构布局优化方法。

1 问题描述

1.1 质量矩飞行器基本构型

文中质量矩飞行器采用3个滑块的控制方式，其布局构型如图2所示。

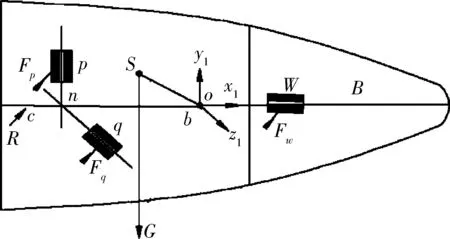
图2 质量矩飞行器基本构型图

飞行器由弹体和径向滑块p，q，轴向滑块w组成。图中的滑块p，q，w的导轨分别平行于弹体坐标系b-xbybzb的yb，zb，xb轴。任一时刻的质心用S表示。建模过程中认为滑块为质点，不考虑其转动特性。相关符号定义如表1所示。

表1 符号参数说明表

1.2 质量矩飞行器动力学模型

弹体B、滑块p、滑块q、滑块w和系统S的质量之间的关系为：mS=mB+mp+mq+mw。定义滑块p、滑块q、滑块w的质量比分别为：

μp=mp/mS，μq=mq/mS，μw=mw/mS

弹体相对于地面坐标系的角速度在体坐标系下分解为：

弹体质心的速度在体坐标系分解为：

滑块p，滑块q和滑块w在弹体内的位置矢量为：

,,

式中：lp，lq分别表示滑块p和滑块q的轴向坐标；δx，δy和δz分别表示滑块w的轴向偏移量和滑块p，滑块q的横向偏移量。则系统质心s在弹体内的位置矢量为：

rbs=μprbp+μqrbq+μwrbw

(1)

空气动力以及地球引力在体坐标系下的分量分别为：

,

空气动力对弹体质心b的气动稳定力矩以及阻尼力矩在体坐标系下的分量分别为：

,

弹体对质心b的转动惯量矩阵为：

则飞行器质心运动和绕质心转动的动力学方程可表示为：

ω1×V1

(2)

Mfq+Mfu+Mft

(3)

其中：

×rbi

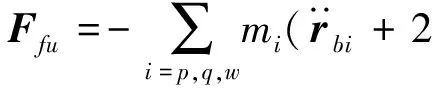
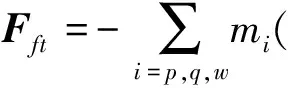
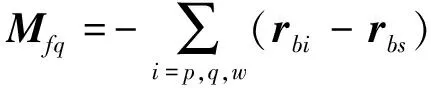
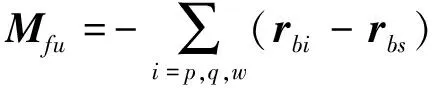
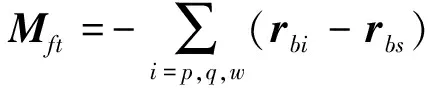
(·)和(··)分别表示在体坐标系下对时间的一阶导数和二阶导数。定义Ffq和Mfq分别为附加切向力和附加切向力矩，Ffu和Mfu分别为附加伺服力和附加伺服力矩，Fft和Mft分别为附加离心力和附加陀螺力矩。

2 压心测量误差情况下的气动稳定力矩表达式

压心是总的气动力的作用线与导弹纵轴的交点。在攻角不大的情况下，常近似地把总升力在纵轴上的作用点作为全弹的压力中心[11]。对于高马赫数的导弹，假设某弹头长细比fn=1.5，利用文献[12]中的经验公式并查表拟合，可得压心系数与攻角和马赫数的关系如图3所示。

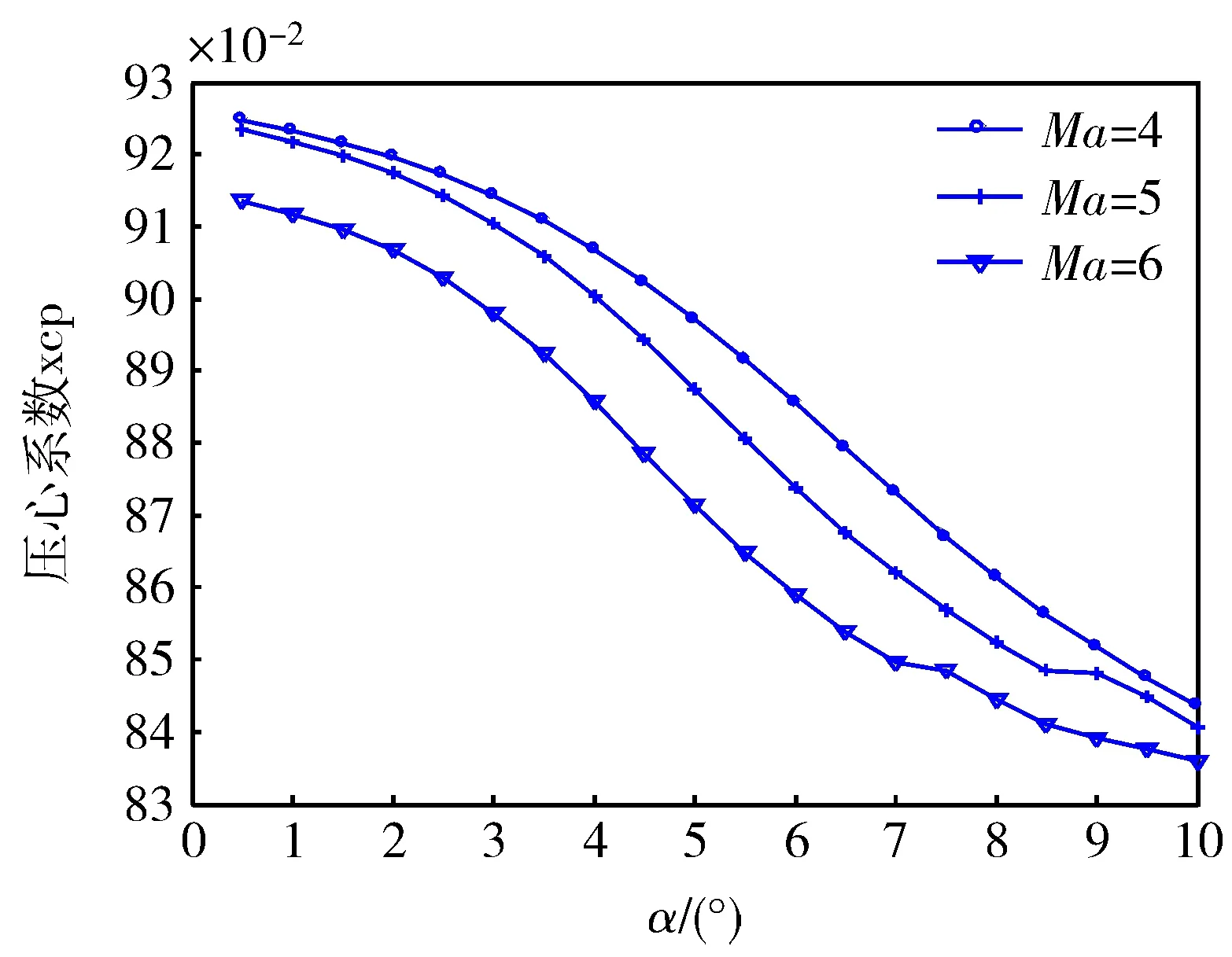
图3 压心系数与攻角马赫数的关系图

从图3中可以得出以下结论：1)随着导弹马赫数的增加，导弹的压心系数呈逐渐降低的趋势；2)随着攻角的增加，压心系数也呈逐渐减小的趋势；3)合理设计导弹的外形(头部长细比fn，全弹长细比fB等结构参数)可以减小压心系数的变化。

下面给出压心不确定情况下气动稳定力矩的表达式。由气动稳定力矩的定义可知：系统的气动稳定力矩表达式为：

MR=rsc×R1=(rbc-rbs)×R1

(4)

其中：设rsc为从系统质心s到压心c的位置矢量，rbc为从弹体质心到压心的位置矢量，在弹体坐标系下的分量为：

(5)

式中：xb为弹体质心到头部的距离，xc为标称状态下压心到弹体头部的距离，Δxc，Δyc和Δzc分别为压心轴向、径向的位置偏差。将式(1)和式(5)代入气动稳定力矩的表达式(4)中得：

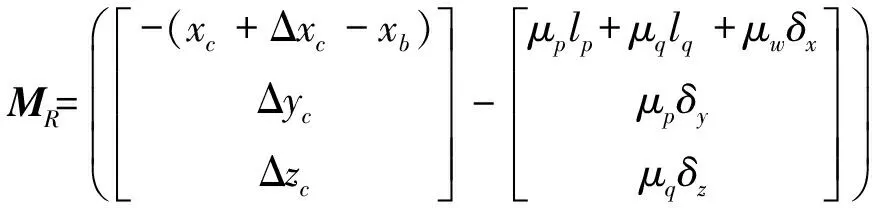
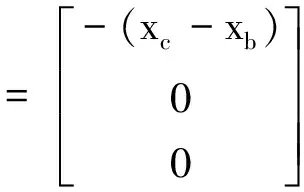
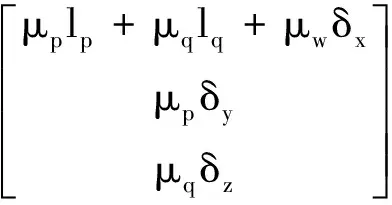
(6)

=MsR+MΔR+MfR

由上式可知，弹体所受的气动稳定力矩MR是由常规气动稳定力矩MsR、压心偏差气动稳定力矩MΔR和由质量块位置变化产生的附加气动稳定力矩MfR组成。对于外形参数确定的质量矩导弹，姿态控制性能除了与3个滑块的质量参数和运动规律有关，还与压心的位置偏差有关。压心偏差气动稳定力矩的表达式为：

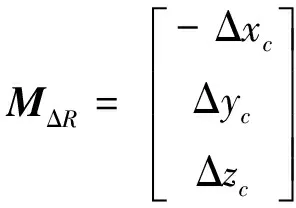
(7)

为了方便分析变质心飞行器压心系数对其控制性能的影响，本文暂不考虑各通道的气动交联耦合现象，仅仅对每个通道进行单独分析。从式(7)中可以看出：压心的轴向位置偏差主要影响俯仰和偏航通道的气动稳定力矩，而不影响滚转通道的气动稳定力矩。压心沿体轴y1轴的径向偏差主要影响滚转通道和俯仰通道的气动稳定力矩，而对偏航通道的气动稳定力矩没有影响。压心沿体轴z1轴的径向偏差对飞行器的影响与y1轴类似。由于工程上一般不考虑压心的径向偏差，认为Δzc≈0,Δyc≈0。则将式(7)化简，得到压心偏差产生的气动稳定力矩为

(8)

定义附加气动稳定力矩MfR=rbs×R1，是由滑块参数及运动状态决定的力矩。若压心偏差范围较大，则无法判断弹体姿态的改变是来自于压心偏差气动稳定力矩，还是附加气动稳定力矩，无法形成正确的控制指令。因此，研究压心位置偏差对质量导弹控制效能的影响，并定量地给出压心最大的容许偏差范围和滑块质心最小移动空间，是十分有意义的。下面进一步研究压心不确定性对质量矩飞行器控制性能的影响。

3 压心测量误差对质量矩飞行器总体参数的要求分析

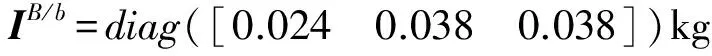
当压心系数的变化为1%时，压心系数偏差对系统的影响结果如图4所示。由式(8)可知：压心的轴向位置偏差主要影响飞行器的俯仰和偏航通道，不过由于附加转动惯量的存在，会使得俯仰和偏航通道对滚转通道有一定的耦合作用，也会使得滚转通道产生一点偏差，但相比来说，影响会很小。

图4 压心系数偏差为1%时飞行器姿态偏差曲线

从图4中可以看出：压心系数偏差对攻角和侧滑角影响很大，配平攻角的偏差约为14.39%，配平侧滑角的偏差约为13.59%，法向过载的偏差约为14.21%，这说明，压心系数偏差严重影响了质量矩控制的性能，使得控制系统的设计变得极其困难。而压心系数偏差对滚转角的影响相对来说较小，在控制系统设计的时候可以忽略其影响。

文献[2,5]分别采用不同方法对变质心控制机理进行了研究，建立了滑块运动与配平攻角之间的关系，但其中文献[2]针对的是单滑块模型，文献[5]针对的是双滑块模型。本文运用了上述两文献中的方法将其推广到三滑块模型，并进一步得到了配平攻角、配平侧滑角与压心系数的解析关系：

(9)

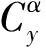
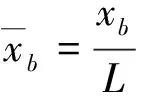
(10)

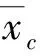
式(9)给出了配平角与压心系数之间的解析关系。不妨设

,

(11)

则式(9)可简化为：

(12)

(13)

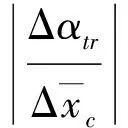
3.1 设计滑块导轨在弹体内位置

布局A：两径向滑块的滑道配置在弹体质心的后部，取lp=lq=-0.04m。

布局B：两径向滑块的滑道配置在飞行器的前鼻部，取lp=lq=0.20m。

在压心系数偏差为1%的情况下，布局A的仿真结果如图4所示，布局B的仿真结果如图5所示。

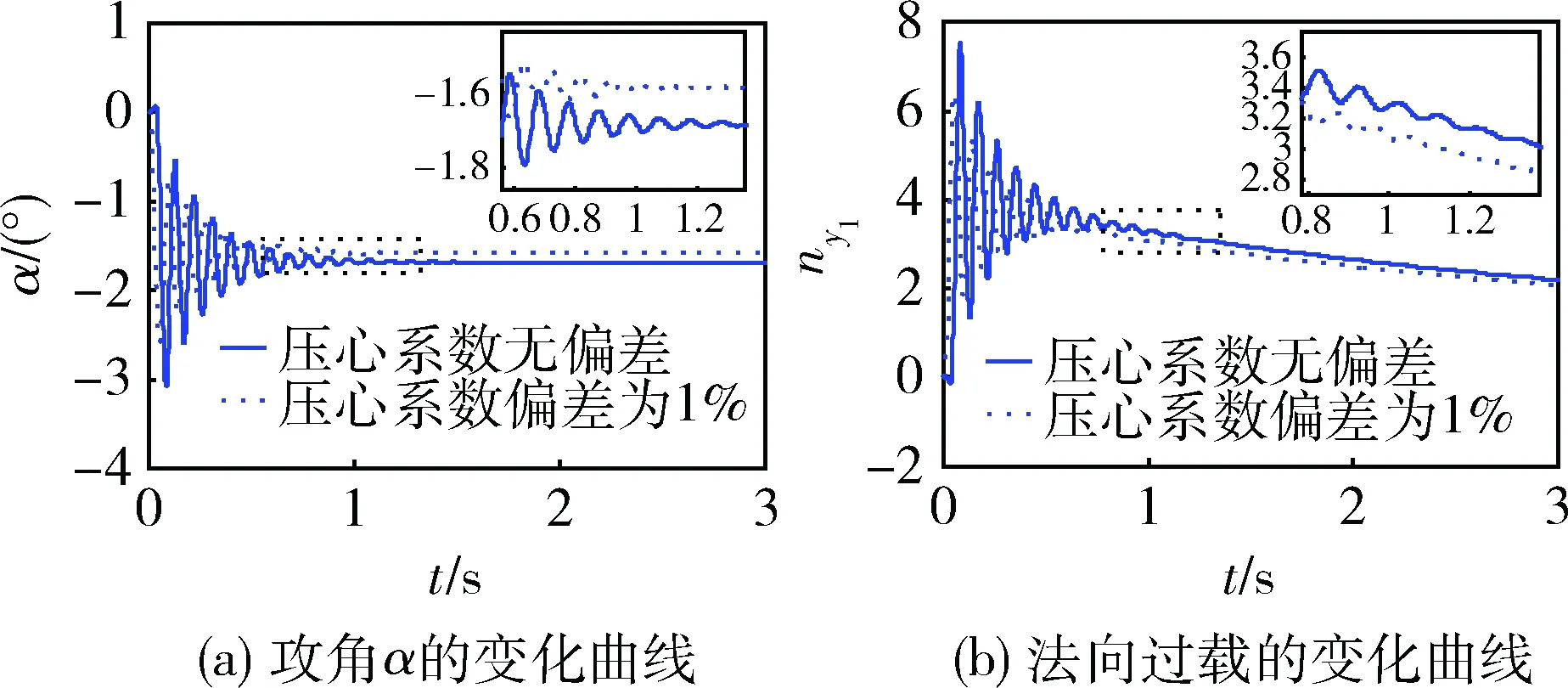
图5 采用布局B的优化结果

从图5中可知，飞行器采用布局B后，压心系数偏差对质量矩控制的影响明显减小，攻角误差由原来的14.39%减小到优化后的5.88%，法向过载由原来的14.21%减小到优化后的5.93%。

3.2 三滑块位置协调控制

对于内部结构布局已经确定的飞行器，由式(9)可知，配平角(αtr,βtr)是滑块控制量(δx,δy,δz)的函数，对于一个系统期望的配平角，可以通过选取不同组(δx,δy,δz)的值来产生这个配平角。将方程(9)作为变量(δx,δy,δz)条件约束方程，目标最优函数为

(14)

其中

,,

根据式(9)和(14)可知，在设计活动质量块的运动规律时，减小控制量δy，δz的值，控制轴向滑块的运动规律δx>0且增大δx的值，也可以减小压心不确定性对飞行器控制性能的影响。因此，在根据任务指标设计活动质量块的运动规律时，合理地选取各滑块沿滑道的位移，也可以在一定程度上解决压心不确定性问题。下面通过一个具体的算例，说明该方法的有效性。

任务目标：飞行器产生-1°的指令配平攻角，不产生配平侧滑角，即αtr=-1°,βtr=0°。飞行器内部活动质量块布局采用上节所述的布局B方式。各滑块均按正弦规律运动到如表2所示的指定位置，响应时间为0.4s。仿真结果如表2和图6～7所示。

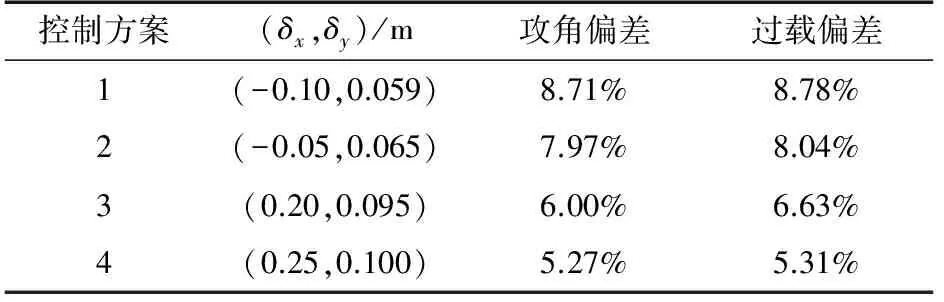
表2 滑块控制方案及仿真结果

图6 基于方案1的优化结果

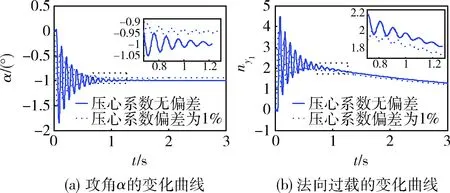
图7 基于方案4的优化结果

从上述仿真结果中可知， (δx,δy)=(0.25,0.1000)这个组合的姿态偏差最小，说明在本例子中，δx调节的作用要大于δy的调节作用，也就是说本例子中通过增大δx值来降低压心对系统影响的方案要优于通过减小δy值来降低压心对系统影响的方案。所以，通过合理地协调配置(δx,δy)，可以使得压心系数偏差对质量矩控制的影响一定程度上的减小。攻角误差由原来的8.71%减小到优化后的5.27%，法向过载由原来的8.78%减小到优化后的5.31%。

3.3 压心最大容许偏差范围

当任务目标给定时，通过所给定的配平角的允许指标Δαtr和Δβtr可以确定压心最大容许偏差范围，由式(13)可得

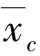
(15)

从前两节中可以看出，虽然通过优化弹体内部活动质量块的结构布局和合理设计控制变量(δx,δy,δz)的大小，可以减弱压心不确定性对飞行器的影响。不过，由于飞行器结构外形的限制，滑块结构布局参数可调节范围有限，压心偏差对飞行器仍然有很大的影响。为了实现质量矩技术，当压心偏差超过最大的容许偏差范围的时候，应当根据输出量的反馈信息适当的调节压心。在工程实际应用上，对于无翼式导弹，通常采用安装安定尾翼的方法调整压心[14]。这种尾翼应具有比较小的面积和弦长，以保证压心系数的变化很小。

由于空气动力R1的值较大，即使压心偏差很小(压心系数偏差为1%时)都会使气动力矩变得很大，严重影响飞行器的控制性能。与其它的传统控制方式不同，质量矩控制对飞行器压心最大容许偏差范围和执行机构的结构布局等总体参数提出了更高的要求。为了提高质量矩飞行器控制性能，必须将总体参数优化与先进控制器设计两种途径紧密结合。

4 结论

通过理论计算或风洞试验获得的标称压心点与飞行器实际飞行中的实际压心点存在着偏差，对质量矩飞行器的稳态姿态角的影响很大。本文对质量矩控制中的压心不确定性问题进行了理论分析，尤其针对压心偏差对控制性能的影响进行了较深入的研究：将径向滑块的滑道尽量配置在飞行器的前鼻部，合理的设计质量矩的控制量(δx,δy,δz)等措施都可以减小压心不确定性对质量矩控制的影响。在压心偏差超过最大容许偏差范围的时候，可以采用对压心的主动控制的方式来保证质量矩控制的精度。质量矩控制作为一种新颖的控制模式，在工程应用上还面临着很多问题，本文的研究工作仅仅是初步的，可为今后质量矩控制技术的实际应用提供一些借鉴。

参 考 文 献

[1] Vaddi S S, Menon P K, Sweriduk G D.Multistepping Approach to Finite-Interval Missile Integrated Control [J].Journal of Guidance, Control, and Dynamics, 2006,29(4):1015-1019.

[2] Robinett, R D III, Sturgis B R, Kerr S A.Moving Mass Trim Control for Aerospace Vehicles[J].Journal of Guidance,Control,and Dynamics,1996,19(5):1064-1070.

[3] Menon P K, Sweriduk G D, Ohlmeyer E J, Malyevac D S.Integrated Guidance and Control of Moving-Mass Actuated Kinetic Warheads [J].Journal of Guidance, Control, and Dynamics, 2004, 27(1):118-126.

[4] 廖国宾，于本水，杨宇光.质量矩控制技术的机理分析及方程简化研究[J].系统工程与电子技术,2004, 26(11):1635-1639.(Liao Guo-bin,Yu Ben-shui,Yang Yu-guang. Study on the Theory and Simplified Equations of Mass Moment Control Missile [J].Systems Engineering and Electronics，2004, 26(11):1635-1639.)

[5] 李瑞康，高长生，荆武兴，等．飞行器变质心控制及性能分析[J].宇航学报，2010, 31(9):2165-2171.(Li Rui-kang, Gao Chang-sheng Jing Wu-xing，et al．Moving Mass Control and Performance Analysis for Aerospace Vehicl [J].Journal of Astronautics, 2010, 31(9): 2165-2171.)

[6] 周韬，黄运平，陈万春, 殷兴良.导弹质量矩控制技术建模与静态性能分析[J].宇航学报,2006, 27(5):1081-1086.(Zhou Tao, Huang Yun-ping, Chen Wan-chun,Yin Xing-liang.Dynamics Modeling and Static Capability Analyze of Moving Mass Trim Con-trol of Missile [J].Journal of Astronautics，2006, 27(5):1081-1086.)

[7] 周凤岐，崔利明，周军.弹道式导弹弹头变质心机动控制[J].宇航学报, 2000, 21(增刊):107-110.(Zhou Feng-qi, Cui Li-ming, Zhou Jun.The Control of Ballistic Warhead with Variable Centroid [J].Journal of Astronautics, 2000,21(s):107-110.)

[8] 张晓宇，贺有智，王子才.质量矩拦截弹的模糊滑模姿态控制系统设计[J].宇航学报,2006, 27(6):1419-1423.(Zhang Xiao-yu, He You-zhi, Wang Zi-cai.Fuzzy Sliding Mode Attitude Control Ap-proach to Mass Moment Interception Missile [J].Journal of Astronautics,2006, 27(6):1419-1423.)

[9] 秦莉，杨明，郭庆.遗传算法在质量矩导弹姿态控制中的应用[J].北京航空航天大学学报, 2007,33(7):769-772.(Qin Li, Yang Ming, Guo Qing.Moving-mass Attitude Control Law Based on Genetic Algerithm[J].Journal of Beijing University of Aero-nautics and Astronautics, 2007,33(7):769-772.)

[10] 孙卫华, 李高风.移动质心再入飞行器姿态的无源性控制[J].宇航学报, 2008, 29(4):1314-1319.(Sun Wei-hua, Li Gao-feng.Attitude Control of Moving Mass Reentry Vehicle Using Passivity-base Tech-niques.Journal of Astronautics, 2008, 29(4):1314-1319.)

[11] 钱杏芳，林瑞雄，赵亚男.导弹飞行力学[M].北京: 北京理工大学出版社, 2008:171-174.

[12] 叶尧卿.便携式红外寻的防空导弹设计[M].北京: 中国宇航出版社, 2006:441-448.

[13] 孙文景, 李志明.导弹防御与空间对抗[M].北京:原子能出版社, 2004:145-153.

[14] 于云峰，杨军，杨晨，等.无翼式推力矢量控制导弹总体规划方法研究-重心及压心规划[J].西北工业大学学报, 1998, 16(1):42-46.(Yu Yun-feng,Yang Jun, Yang Chen, et al．On Proper Consideration of Center of Gravity and Pressure Center in Design of Air-to-Air Missile [J].Journal of Northwestern Poly-technical University, 1998, 16(1):42-46.)