基于H-矩阵/QFT的鲁棒解耦多变量控制在SRLV姿态控制中的应用

赵志芳 肖利红 倪少波

北京航天自动控制研究所, 北京 100854

重复使用亚轨道飞行器(Sub-Orbital Reusable Launch Vehicle， SRLV)作为集成运载火箭、航天器、航空器(无人机)等多项技术的复杂飞行器，飞行状态和参数变化范围很大，控制对象具有强非线性、强耦合、快时变、不确定性等特点[1-2]。传统的控制器设计方法是不考虑俯仰、偏航、滚转三通道之间的任何交连作用，独立设计控制器，然后加入协调控制支路对交联耦合项进行补偿。本文基于H-矩阵并结合定量反馈理论(QFT)中的自动整形原理设计鲁棒解耦控制器。

传统的解耦方法通常是针对精确的对象模型，设计预补偿器来解耦。模型对象存在不确定时，不能保证有良好的解耦效果，且解耦结果对频率敏感。本文提出的基于H-矩阵理论针对具有参数不确定性的对象模型，设计反馈补偿器，这就保证MIMO系统在具有参数不确定性时几乎是解耦的，因此，我们可以称之为鲁棒解耦技术。反馈补偿器的具体实现是利用QFT自动整形原理，从而保证了解耦结果对频率的不敏感性和对模型参数不确定性的鲁棒性。

1 H-矩阵/QFT鲁棒解耦多变量控制设计原理

1.1 问题提出

图1所示为H-矩阵/QFT鲁棒解耦多变量控制系统框图，其中G(s)为被控对象，G≡G(α,s)=(gij(α,s))表示带有不确定性参数向量α的线性时变传递函数。K(s)为反馈补偿器，F(s)为控制器，H(s)为反馈补偿后几乎解耦的被控对象。

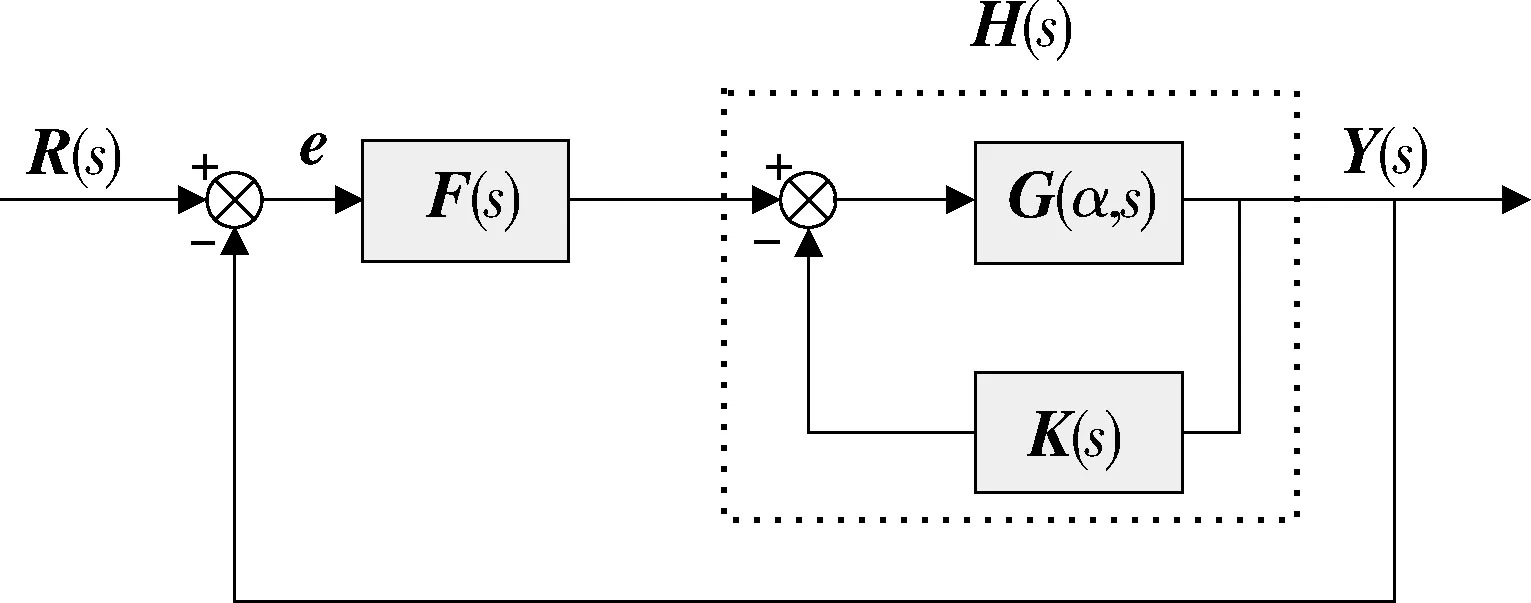
图1 H-矩阵/QFT鲁棒解耦多变量控制系统

理想状况下，设计目的是寻求反馈补偿器K(s)，使得G(α,s)补偿后的系统H(s)成为具有如下形式的对角系统：

H(s)=diag[h1(s),h2(s),…,hn(s)]

(1)

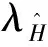
(2)

系统是几乎解耦的[3]，这样就可以把一个多变量系统的设计问题简化为由该系统的各对角元构成的单变量系统的设计问题，从而达到简化控制器结构的目的。

1.2 反馈补偿器设计

1.2.1 反馈补偿器K(s)设计原理[3]

由图1可得如下传递函数

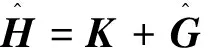
(3)

鲁棒解耦的目标是确定对角阵K(s)，使得满足公式(2)。

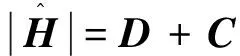
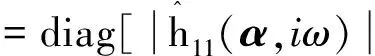
(4)

ρ≤

(5)

其中，C+为C∈Cn×n的模矩阵，即：C+≡(|cjk|),j,k=1,2,…,n，同理可得D+。将公式(3)带入公式(5)可得

≥

(6)

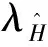
为了便于应用QFT的设计原理，将公式(6)变为如下形式：

≥

∀α∈Ω

(7)

其中，

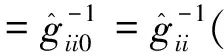
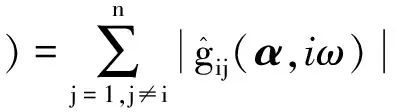
(8)

1.2.2 QFT自动整形原理设计kii(s)

鲁棒控制理论中的定量反馈理论(QFT)是一种基于频域的鲁棒控制设计理论，QFT在设计控制器之前各种不确定性和需要达到的性能指标以定量的形式描述出来，然后根据这些限定，设计可以容忍这些不确定性并且满足性能指标的控制器，设计的核心环节就是确定设计指标,构造对象模板,在Nichols图上生成复合频域边界,根据复合频域边界设计控制器F(s)，即在Nichols图上对标称对象进行整形的过程[4]。

本文利用QFT对参数不确定性和对频率不敏感性的优势，来设计kii(s)。将公式(7)作为性能指标，将其转换成Nichols图上的频率边界，然后根据这些频率边界设计kii(s)，使得到的Li0=kipi0频率响应曲线应在边界上方,并且应尽可能与边界靠拢。本文利用遗传算法进行自动整形[5]。

2 H-矩阵/QFT鲁棒解耦多变量控制在SRLV姿态控制系统中的应用

2.1 SRLV小偏差线性模型

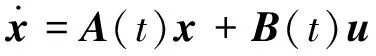
y=Cx

(9)

其中,

x=[Δωz1Δωy1Δωx1ΔαΔβΔν]T

(10)

ωz1,ωy1,ωx1分别为俯仰角速度，偏航角速度，滚转角速度;α,β,γ分别为攻角，侧滑角，滚转角;C=[O3I3]。截取某一段飞行区域，飞行条件和状态如表1。

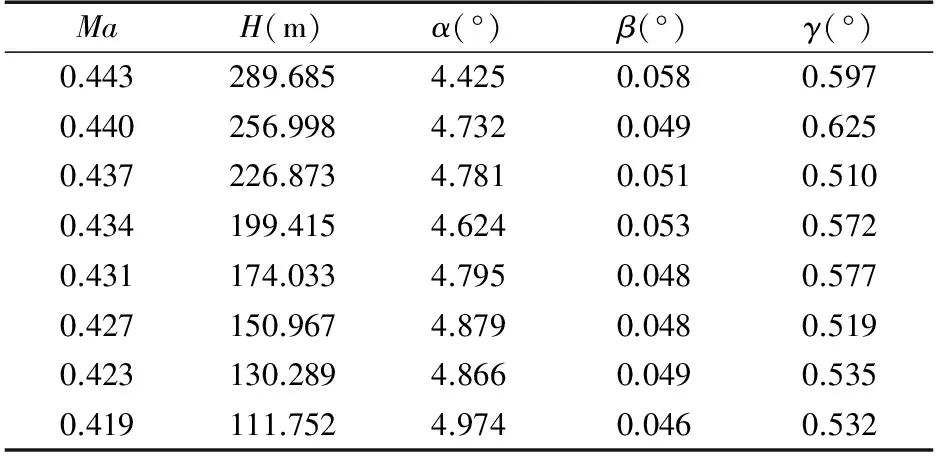
表1 飞行状态表

得到传递函数为如下形式的3×3的传递函数矩阵：

(11)

2.2 反馈补偿器K(s)及控制器设计

由于俯仰通道本身具有对角优势。根据1.2.2节中所述的QFT中性能指标转换成频域边界的原理，得到如图2偏航通道和图3滚转通道频域边界。由于在频域边界图中各个频率的边界形成考虑了参数不确定性的影响，因此，得到的解耦结果对参数不确定性和频率不敏感。

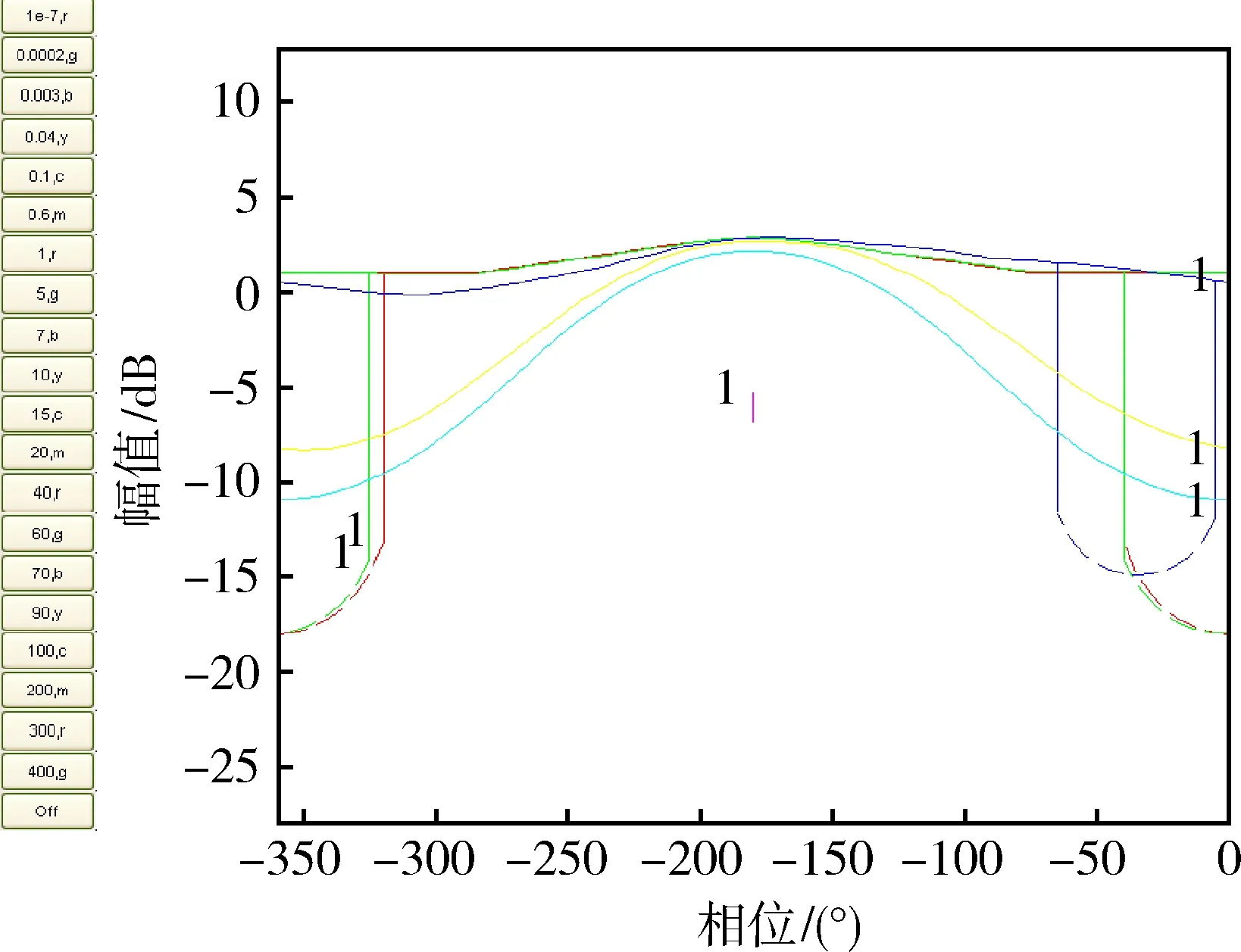
图2 偏航通道频域边界

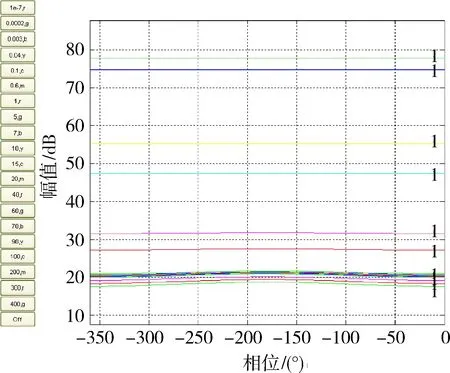
图3 滚转通道频域边界

根据频域边界，基于遗传算法对标称模型进行自动整形，得到反馈补偿器为K(s)=diag[k1(s),k2(s),k3(s)]，其中

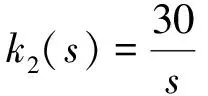
(12)

图4分别为具有不确定性参数特性的偏航和滚转通道补偿前后的对角优势度图。

2.3 控制系统仿真及结果分析

针对图1所示的解耦后的控制对象H(s)设计控制器，

F(s)=diag[f1(s),f2(s),f3(s)]

(13)

图5、图6和图7分别为关于攻角α、侧滑角β和滚转角γ的波特图和阶跃响应图。从仿真结果可以发现，该方法对系统的解耦是成功的，控制效果也是比较好的。

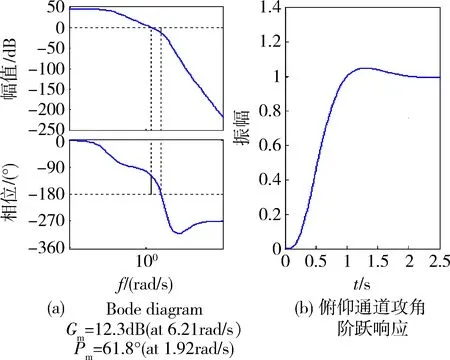
图5 俯仰通道控制结果图

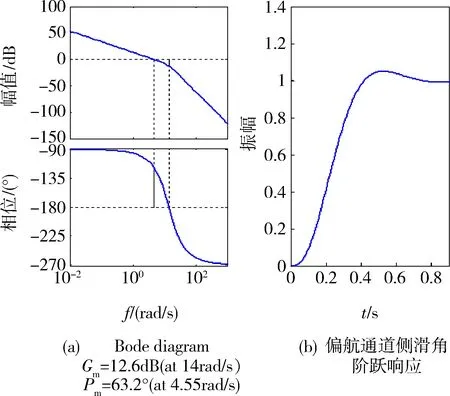
图6 偏航通道控制结果图

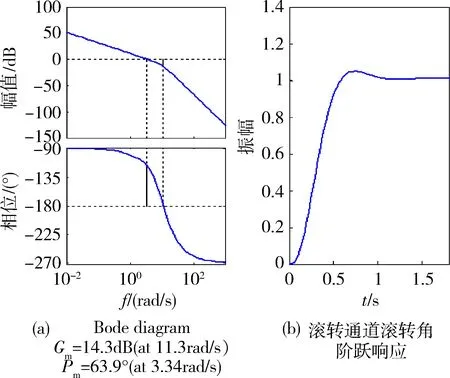
图7 滚转通道控制结果图

3 结论

仿真研究表明，本文提出的采用H-矩阵和定量反馈理论(QFT)相结合设计鲁棒解耦控制器，能够有效地将非对角优势系统转化为对角优势系统，且解耦结果对参数不确定性和频率不敏感。将该方法应用到SRLV再入返回控制系统设计中，使三通道相互耦合的系统简化为三个单通道系统，从而降低控制器设计难度及复杂度。该方法用于 SRLV再入返回三通道的解耦控制是可行和有效的。

参 考 文 献

[1] 杨勇.我国重复使用运载器发展思路探讨[J].导弹与航天运载技术,2006，(4)：1-4.(Yang Yong.Study on Roadmap of Chinese Reusable Launch Vehicle[J].Missiles and Space Vehciles,2006(4):1-4.)

[2] 吴了泥.可重复使用运载器亚轨道再入段制导与控制技术研究[D].南京航空航天大学博士论文，2009.

[3] Nwokah O D I ，Nordgren R E，Grewal G S . Inverse Nyquist Array： a Quantitative Theory [J].IEE Proceedings：Control Theory and Applications，1995，142 (1) ： 23-30.

[4] 王增会,等.定量反馈理论发展综述[J].控制理论与应用，2006,(3)：403-410.(Wang Zenghui.Survey of the Development for Quantitative Feedback Theory[J].Control Theory & Applications,2006,(3):403-410.)

[5] Mario Garcia-Sanz，Carlos Molins.Advanced Quantitative Robust Control Engineering: New Solutions for Automatic Loop-Shaping for SISO and MIMO Systems[R].Universidad Publica De Navarra Pamplona (SPAIN) Dept De Automatica Y Computacion，2009,9,1.