渐近均匀化方法在土钉支护变形中的应用

吕 弦, 马石城



渐近均匀化方法在土钉支护变形中的应用

吕 弦, 马石城

(湘潭大学 土木工程与力学学院, 湖南 湘潭, 411105)

利用FLAC-3D建立模型, 结合渐近均匀化方法求得了土钉和土组合成的复合体的等效模量, 并对土钉支护的变形性能进行了分析. 通过与实测结果的对比, 验证了采用渐近均匀化方法对土钉支护变形进行分析是可行的.

土钉支护; 均匀化方法; FLAC-3D; 基坑

土钉支护, 在我国也被称为作土钉墙或者锚喷网支护墙, 同传统意义上的锚喷支护相比, 土钉支护布置较密且沿锚杆全长注浆; 一般不施加预应力, 或直接将金属杆打入土体, 施工简单易行, 经济可靠. 土钉支护是上世纪70年代发展起来的一项新的挡土技术, 它被应用于基坑开挖及边坡稳定[1]. 其施工过程为: 将土钉以一定的方式打入土体中, 对原位土体进行加固, 然后在基坑开挖面或边坡表面挂上钢筋网, 喷上混凝土[2]. 土钉墙具有造价低廉、施工速度快等优点, 被广泛应用于基坑维护、边坡加固等工程中, 国内外学者对土钉墙的性状和作用机理做了大量的研究和探索, 深化了对土钉墙的认识和理解. 随着城市建设的加速发展, 对基坑变形的要求越来越高, 基坑支护结构设计方式由以强度控制为主转变为以变形控制设计为主.

均匀化方法在上世纪发展起来并应用于复合材料领域中, 用其分析复合材料的细观与宏观性能,目前在国际上较流行. 材料一般具有非均质性的特点, 均匀化理论能根据这一特点, 从宏细观两个尺度对材料的力学性能进行分析. 即均匀化理论可以从宏观方面对结构的响应进行分析, 也可以从细观方面对材料的变形及等效模量进行分析[3]. 本文结合均匀化理论对土钉支护基坑的变形进行分析.

1 均匀化理论

均匀化理论基本思想是: 从具有周期性微结构的非均质材料中选出具有代表性的一个体积单胞, 通过对代表性单胞的研究, 反映整个结构的性质, 即将材料的细观性质与宏观性质相结合. 通常在非均质材料中所选出的一个代表性单胞, 只是非均质材料中的一个点, 应用均匀化方法对非均质材料的研究过程中单胞的选取如图1所示.

1.1 均匀化理论推导过程

图1 周期性非均匀材料及单胞

对于一个代表单元体REV, 可定义其平均应力, 平均应变及本构模型为:

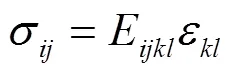
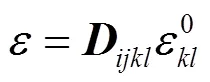
推导如下:

将上式写成:

1.2 弹性常数的求解

结构在静态时, 满足下列基本方程:

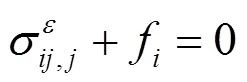
及边界条件:

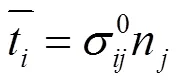
材料的弹性常数张量分量为:

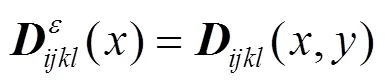
位移函数也可表示为:

在线弹性范围内, 用虚功原理表示的控制方程为:

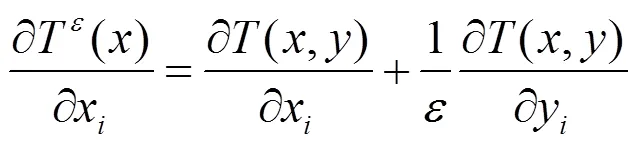
将式(16)代人式(15), 并考虑式(18), 经推导可求解出材料的等效弹性常数[4], 即:

2 均匀化求解及数值分析

2.1 工程概况

该工程场地的土层主要为砂质粉土和粉质粘土, 基坑垂直开挖深为9 m, 分成5步开挖完成, 每步开挖的深度为1.8 m. 土钉采用钻孔注浆钉, 直径100 mm, 设计长度6.1 m, 自上而下设置为5排, 与水平线之间的夹角为20°, 土钉水平间距为1.8 m, 竖向间距为1.8 m. 距离地面以下18 m处分布有地下水, 所采用参数如下.

土体的参数: 内聚力= 15 kPa, 内摩擦角= 25°,膨胀角= 25°, 密度= 1800 kg/m3, 泊松比= 0.3; 土钉参数: 等效模量eq= 3.825×104MPa, 密度= 2400 kg/m3, 泊松比= 0.3; 面层参数: 等效模量eq= 2.6×104MPa, 密度= 2 500 kg/m3, 泊松比=0.3; 重力加速度= 9.8 m/s2, 地面超载5 kPa.

2.2 均匀化求解

土钉是成一定角度打入土体中的, 为简便计算, 将土钉在水平方向投影, 取其投影长度作为土钉在土体中的分布长度. 根据土钉的实际布置情况, 选取计算单胞(图2)的长宽高, 其分别为1.8 m、1.8 m、5.7 m.

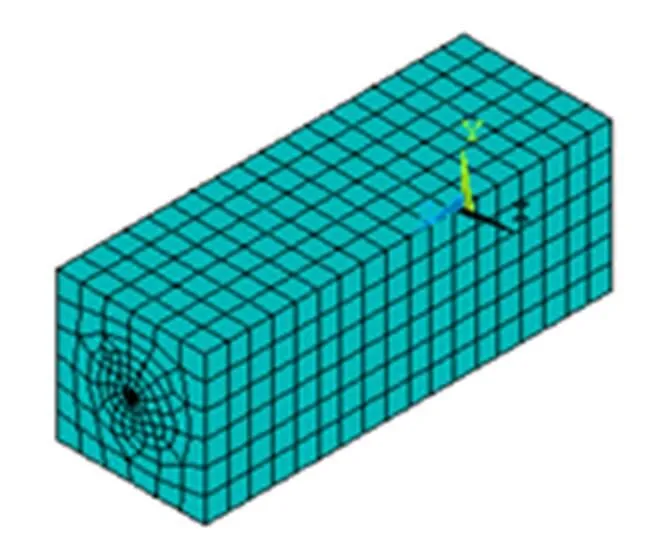
图2 土钉支护单胞有限元模型

利用渐近均匀化理论对周期性复合体的线弹性有效弹性模量的求解步骤为: ① 确定周期性复合体组成部分, 并选取基体及增强体的性能参数; ② 对结构体的周期性单胞建立有限元模型, 并提取单元信息及单元节点信息; ③ 编程, 解细观均匀化有限元问题, 得到细观位移; ④ 将步骤③中所求得的细观位移代入宏观结构的有效性能常数有限元, 求解方程, 并解得宏观有效弹性常数.

土体的变形模量随正应力增大而增大, 为了考虑土体的这一性质, 参考Duncan-Chang模型选取土体的弹性模量. 进行均匀化计算时将基坑土层按开挖步数取5个单胞, 代人不同参数进行计算, 计算结果为: 第1步开挖到第5步开挖所选取单胞的等效模量分别为: 110.68 Mpa、129.41 Mpa、146.27 Mpa、162.01 Mpa、176.98 Mpa.泊松比均为0.3.

2.3 基于FLAC-3D的数值分析

FLAC-3D软件是面向土木工程、交通、水利、石油及采矿工程、环境工程的通用软件, 其在岩土工程界具有广泛的影响. 本文应用FLAC-3D对土钉支护基坑的开挖过程进行数值模拟, 计算模型及网格划分如图3所示.

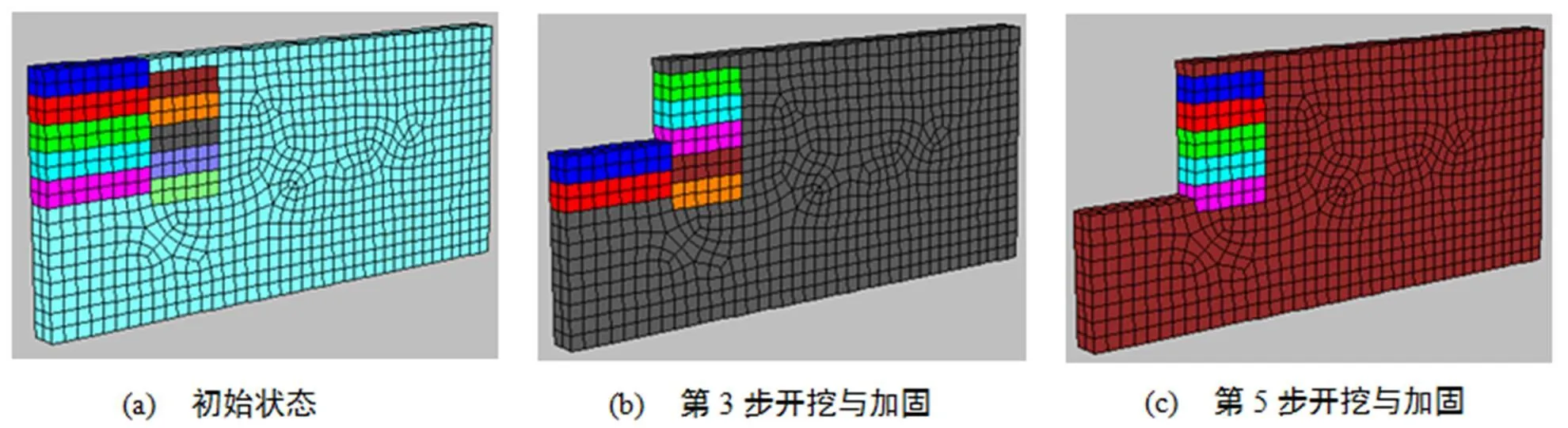
图3 计算模型及网格划分

选取一列土钉进行模拟, 即模型宽为1.8 m, 高取18 m, 长取为40 m. 土体采用Mohr-Coulomb弹性-完全塑性模型, 对于开挖后插入土钉的加固体采用弹性模型. 所选取的模型与周围的土体之间存在一定约束, 因此模型的边界条件选为: 最底面设为固定铰支, 竖直向不设置约束可自由滑动, 4个侧面均设置为滚动支座.

3 计算结果

本文引用渐近均匀化理论用FLAC-3D模拟基坑开挖过程, 施工过程分5步开挖, 每开挖1层后,通过变换加固区的弹性模量代替土钉的插入. 通过软件的分析, 与实测结果进行对比, 结果如图4所示. 从图中可知水平位移随离坡面的距离增大而减小, 最大值发生在开挖面.

图4 基坑水平位移云图

计算所得坡顶位移为9.7 mm, 实测坡顶位移为10.3 mm, 就本文分析的结果看, 实际位移略大于基于渐近均匀化理论的数值分析结果, 但总体来看, 两者结果基本吻合.

4 结论

本文将渐近均匀化理论引入到土钉支护基坑水平位移的变形分析中, 通过本文的计算与分析, 并与实测结果对比, 结果表明均匀化方法计算钉土复合体的等效弹性模量具有可靠性.

[1] 陈肇元, 崔京浩. 土钉支护在基坑工程中的应用[M]. 2版. 北京: 中国建筑工业出版社, 2000.1-3.

[2] cecs96-97 基坑土钉支护技术规程[S]. 北京: 中国建筑出版社, 1997.

[3] 付海雄, 马石城, 李晓全. 用渐近均匀化方法计算水泥土的等效弹性常数[j]. 湘潭大学自然科学学报, 2006, 28(1): 117-120.

[4] 谢桂兰. 聚合物复合材料多尺度方法的研究[D]. 湘潭: 湘潭大学, 2008.

Application of homogenization theory to deformation analysis of soil nail support

LV Xian, MA Shi-cheng

(College of Civil Engineering and Mechanics, Xiangtan University, Xiangtan 411105, China)

Asymptotic homogenization theory is applied to calculate equivalent elastic modulus of the reinforced area of soil nails and soil into complex. By establishing a simulation model using FLAC-3D and combining with the equivalent elastic modulus, the displacement performance of soil nailing is analyzed. Compared the results with field measured results; the method is feasible.

soil nailing; homogenization method; FLAC-3D; foundation ditch

TU 761.1

1672-6146(2012)01-0066-04

10.3969/j.issn.1672-6146.2012.01.018

2012-03-10

吕弦(1985-), 女, 研究生, 主要研究方向为土与结构的相互作用. E-mail: xy209lx@163.com

(责任编校:江 河)