分数阶微分方程非零边值问题解的存在性

王翠菁



分数阶微分方程非零边值问题解的存在性

王翠菁1, 2

(1. 中国矿业大学 理学院, 江苏 徐州, 221008; 2. 徐州工业职业技术学院 信息管理技术学院, 江苏 徐州, 221140)

利用压缩映射原理和Krasnoselskii’s不动点定理, 在Banach空间下讨论非线性分数阶微分方程非零边值问题()=(,()), 0<<1;(0)=(0),(1)=β()解的存在性, 其中1<α≤2是一个实数,是Caputo型微分.

压缩映射原理; Caputo型微分; Krasnoselskii’s不动点定理

分数计算[1-3]始于17世纪, 由Leibniz、Euler、Lagrange、Able以及其他人的先驱工作, 才逐步发展起来. 对于分数阶微分方程, 它在不同的科学领域也起着越来越重要的作用[4-6]. 有许多学者在微分方程系统方面已获得不少的研究成果[7-10].

例如, 张淑琴[8]利用锥不动点理论、Leggett-Williams定理讨论了Caputo型分数阶微分方程边值问题:

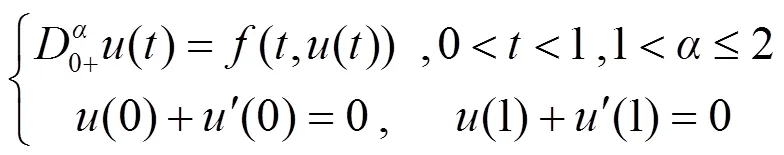
正解及多个正解的存在性.

本文在文献[9-10]的启发下, 在Banach空间下讨论非线性分数阶微分方程非零边值问题()=(,()), 0<<1;(0)=¢(0),(1)=β()解的存在性和唯一性, 其中1<≤2是一个实数,是Caputo型微分, 并且假设是连续的,是Banach空间. 令, 记为在全体连续函数构成的Banach空间赋予其范数(拓扑一致收敛的).

1 预备知识

.

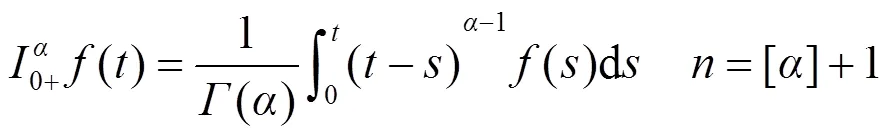
由引理1、引理2可得引理3.

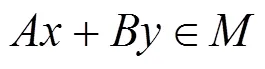
2 主要结论

为了后面的分析, 我们做如下假设:

例如，在班级当中，我们要时刻严格要求幼儿遵守班级中的规章制度，使幼儿懂得制度的不可破坏性和必要性。如对于班级的值日制度，我们要对幼儿进行明确的分工，将每一件事情的责任分配到位，让幼儿在进行简单的值日过程中，明白自己该做什么事，要做什么事等，这种制度化的管理使教师和幼儿都能够轻松完成自己在班级中的责任，从而使幼儿园的班级管理更有秩序，更加简单，使幼儿园的管理质量和水平得到有效的提升和增强。

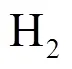
[1] Delbosco D. Fractional calculus and function spaces[J]. J Fract Calc, 1994, 6: 45-53.

[2] Miller K S, Ross B. An introduction to the Fractional calculus and fractional differential equations[M]. New York: Wiley, 1993.

[3] Podlubny I. Fractional differential equations mathematics in science and engineering[M]. New York: Academic Press, 1999.

[4] Oldham K B, Spanier J. The fractional calculus[M]. New York: Academic Press, 1974.

[5] Tatom F B. The relationship between fractional calculus and fractals[J]. Fractals, 1995, 3: 217-229.

[6] Nonnenmacher T F, Metzle R. On the Riemann-Liouville fractional calculus and some recent applications[J]. Fractals, 1995, 3: 557-566.

[7] Bai Z, Lu H. Positive solutions for boundary value problem of nonlinear fractional differential equation[J]. J Math Anal Appl, 2005, 311: 495–505.

[8] Shuqin Zhang. Positive solutions for boundary-value problems of nonlinear fractional differential equations[J]. Electronic Journal of Differential Equations, 2006, 68: 1-12.

[9] Bashir Ahmad. Existence of solutions for fractional differential equations of order q∈(2,3) with anti-periodic boundary conditions[J]. J Appl Math Comput, 2010, 34: 385-391.

[10] Bashir Ahmad, Juan J, Nieto. Existence of solutions for nonlocal boundary value problems of higher-order nonlinear fractional differential equations[J]. Abstract and Applied Analysis, 2009, Article ID 494720: 1-9.

The existence of solutions for nonzero boundary value problem of fractional differential equations

WANG Cui-jing1,2

(1 College of Sciences, China University of Mining & Technology, Xuzhou 221008, China; 2 Information Management Technology Institute, Xuzhou College of Industrial Technology, Xuzhou 221140, China)

By using the contraction mapping principle and Krasnoselskii’s fixed point theorem,we obtain the existence results in a Banach space for nonzero boundary value problem of fractional differential equation()=(,()), 0<<1;(0)=(0),(1)=β(),Where 1<α≤2 is a real number, andis a Caputo′s differentiation.

contraction mapping principle; Caputo′s differentiation; Krasnoselskii’s fixed point theorem

O 175.8

1672-6146(2012)01-0011-03

10.3969/j.issn.1672-6146.2012.01.004

2011-12-15

王翠菁(1982-), 女, 讲师, 研究方向为微分方程边值问题. E-mail: 76124768@qq.com

(责任编校: 刘晓霞)