Note on the augmented eccentric connectivity index
2012-05-09TANGZikaiHOUYaoping
TANG Zi-kai, HOU Yao-ping
Note on the augmented eccentric connectivity index
TANG Zi-kai, HOU Yao-ping
(Department of Mathematics, Hunan Normal University, Changsha 410081, China)


1 Introduction
All graphs in this article are simple and finite. The vertex and edge sets of a graphare() and(), respectively. The degree of a vertexinis denoted by deg() or() for short. The number of vertices ofis denoted by() and it is called the order of. The distanced(,) between two verticesand∈() is the number of edges on a shortest path connectingandin. The eccentricity of a vertexin(); denoted bye() or(), is defined to be max{d(;)|∈}.
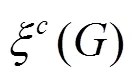
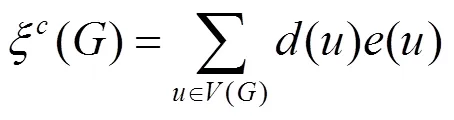
where the summation goes over all vertices of. In [2–6], Gutman et al. gave some mathematical properties of this invariant of graph.
The augmented eccentric connectivity index is an adjacency-sum-distance based index and it is defined as the summation of the quotients of the product of adjacent vertex degrees and eccentricity of the concerned vertex, for all the vertices in a hydrogen-suppressed molecular graph[3]. It is expressed as:

where the summation goes over all vertices of.
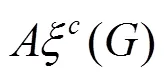
2 The augmented eccentric connectivity index of trees
First we consider the graph1and graph2depicted in Fig.1. These two paths differ only vertex label. In what follows we assume that≥≥1.

Fig.1 Two Paths (a≥b≥1)

Fig. 2 The transformationG1→G2.

By Proposition 2.2, we obtain next proposition easily.


Fig. 3 Two trees T1, T2
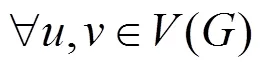


3 The unicyclic graphs with maximum the augmented eccentric connectivity index
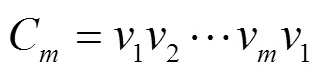
There is at last a number equal or greater than zero between1and2.
Fig. 4 The transformations Tr1, Tr2.
By Lemma 3 and 4, we have:



[1] Sharma V, Goswami R, Madan A K. Eccentric connectivity index: A novel highly discriminating topological descriptor for structure-property and structure-activity studies[J]. J. Chem Inf Comput Sci,1997, 37: 273-282.
[2] Ilic A, Gutman I. Eccentric Connectivity Index of Chemical Trees[J]. MATCH Commun Math Comput Chem, 2011, 65: 731-744.
[3] Bajaj S, Sambi S S, S. Gupta, A K. Model for prediction of anti-HIV activity of 2-pyridinone derivatives using novel topolo- gical descriptor[J]. QSAR Comb Sci, 2006, 25: 813-823.
[4] Doslic T, Graovac A, Ori O. Eccentric Connectivity Index of Hexagonal Belts and Chains[J]. MATCH Commun Math Com- put Chem, 2011, 65: 745-752.
[5] Zhou B, Du Z. On eccentric connectivity index[J]. MATCH Commun Math Comput Chem, 2010, 63: 181-198.
[6] Morgan M J, Mukwembi S, Swart H C. On the eccentric connectivity index of a graph[J]. Discrete Mathematics, 2011, 311:1229-1234.
图的扩展离心连通指数
汤自凯, 侯耀平
(湖南师范大学 数学与计算机科学学院, 湖南 长沙, 410081)


O 221.1
1672-6146(2012)01-0024-04
10.3969/j.issn.1672-6146.2012.01.007
2012-03-18
湖南省教育厅科研项目(08C579).
汤自凯(1973-), 男, 博士, 副教授, 研究方向为图论及其应用. E-mail: zikaitang@163.com
(责任编校:刘刚毅)
