关于不定积分的几种求解方法
2012-05-09赵继红
赵继红
赵继红
(西北农林科技大学 理学院, 陕西 杨凌, 712100)
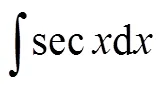
正割函数; 不定积分; 换元积分法

方法1 利用第一类换元积分法[1], 可得:
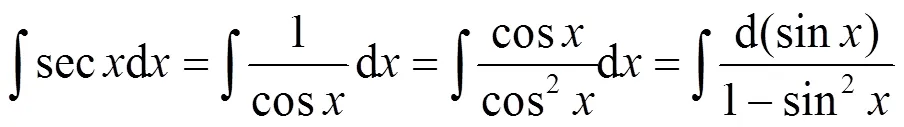
从方法1可以看出, 第一类换元积分法的本质是设法将不定积分中的被积表达式凑成容易求得原函数的形式, 然后进行求解(这也是称其为凑微分法的原因). 基于此, 我们也可以进行如下的凑微分.方法2 观察, 可以进行如下的凑微分[2]:

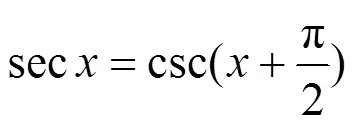
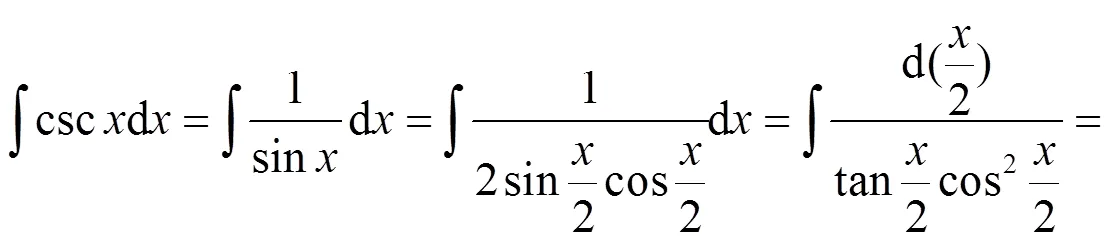
方法3本质上和方法1是一致的, 但是在求解过程中用到了三角函数的恒等变形, 而这些变形在求解三角函数的不定积分中有着十分重要的作用和意义, 合理的变形会大大的简化被积函数的表达式, 从而使得求积分的过程变得简单, 起到事半功倍的作用.
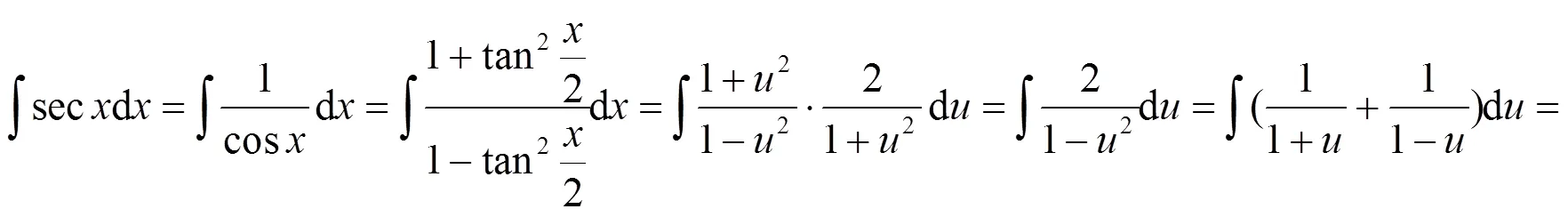
利用万能公式来求三角函数的不定积分是一种十分行之有效的方法, 利用它常常可以将所求不定积分约化为有理函数的不定积分, 从而可以利用有理函数的不定积分理论进行求解(公式法).

相比较而言, 方法5远远比方法1来的复杂, 而且在求解过程中连续利用了两次变量变换.
综上5种方法, 在求解不定积分的题目时, 细心的观察能力和凑微分的能力决定了学生们对题目的把控能力、理解能力和求解能力. 当然, 在求解一般函数的不定积分时, 我们并不能拘泥于使用一种变量替换, 有时候需要做好几次换元过程, 而且也要同时结合分部积分法来求解一些更复杂函数的不定积分. 各种方法的综合和灵活应用才能使得学生更加深刻理解和掌握不定积分这一高等数学中的主要内容.
[1] 华东师范大学数学系. 数学分析(上册). 3版[M]. 北京: 高等教育出版社, 2002: 184-185.
[2] 同济大学数学系. 高等数学(上册). 6版[M] 北京: 高等教育出版社, 2007: 199.

ZHAO Ji-hong
(College of Science, Northwest A&F University, Yangling 712100, China)
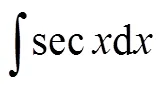
secant functions; indefinite integration; integratal method by substitution
O 13; O 172.2
1672-6146(2012)01-0005-02
10.3969/j.issn.1672-6146.2012.01.002
2011-11-17
西北农林科技大学博士科研启动基金(Z109021118).
赵继红(1982-), 男, 博士, 研究方向: 偏微分方程和生物数学. E-mail: zhaojihong2007@yahoo.com.cn
(责任编校:刘刚毅)
