“胸有成竹”,孕育精彩课堂

张姝

摘要：一切教育教学活动都是为了儿童，教育教学都应从儿童出发，这就是教育的立场。“教材”和“学生”作为教学活动的基本要素，在教师进入课堂教学之前，预案设计之时，应如何基于儿童立场，解读“教材”和“学生”，“胸有成竹”地孕育精彩课堂?笔者分别从教材结构、知识来龙去脉、教材价值追求；学生的学习需求、学习状态、年段特征等方面具体阐述。

关键词：数学教学；教材；学生

中图分类号：G42文献标志码：A文章编号：1673-9094(2012)04-0027-03

毋庸置疑，教育是为了儿童的，教育是依靠儿童来展开和进行的，教育应从儿童出发。这就是教育的立场，因此，教育的立场应是儿童立场。教学的立场同样也应是儿童的立场。

“教材”和“学生”作为教学活动的基本要素，在教师进人课堂教学之前，在进行预案设计之时，应如何基于儿童立场解读“教材”和“学生”，使学生学有发展，使课堂生成智慧，绽放精彩?

笔者长期从事小学数学教学工作，对孕育精彩课堂的“节点”——解读“教材”和“学生”有以下几方面的认识和体会。

一、立足文本——教材，孕育精彩课堂

教材，是教学活动最基本的构成要素之一。教师应当怎样读教材才是基于学生立场呢?

首先，读教材的结构。布鲁纳认为：学习的实质是一个人把同类事物联系起来，并把它们组织成赋予它们意义的结构。不论我们选教什么学科，务必使学生理解该学科的基本结构。这是在运用知识方面的最低要求，这样才有助于学生解决在课堂外所遇到的问题和事件，或者日后课堂训练中所遇到的问题。学习结构就是学习事物是怎样相互关联的。

一年级下册“百以内加、减法”知识编排如下(纵向)：

加法和减法一加法和减法二

两位数加一位数不进位进位

两位数加两位数不进位进位

两位数减一位数不退位退位

两位数减两位数不退位退位

在这两个单元中。计算法则把知识联系起来。基于对知识结构的分析，在教学相关内容时我对教材进行了重组：横向联系教学。让学生不仅学会基本的计算技能，还经历了“由薄到厚，由厚到薄”的结构化过程，发现这些计算之间的内在联系。

其次，读知识的来龙去脉。教材是文本，往往以静态方式呈现结果(结论)或基本计算方法，难以呈现结论的产生过程或计算方法(法则)的形成过程。如果教师也像教材那样处理。学生的学习难以知其所以然。教师需要清晰地知道知识的来龙去脉，才能引导学生发现理解。

《分数除以分数》：量杯里有9／10升果汁，茶杯的容量是3／10升。这个量杯里的果汁能倒满几个茶杯?算式9／10÷3／10。学生可以借助容积单位间的关系转化成整数除法：9／10升=900毫升，3／10升=300毫升，900÷300=3(杯)；可以根据商不变性质转化成整数除法：9／10÷3／10=(9／10x10)÷(3／10xl0)=9÷3=3(杯)，那教材中的算法：9／10÷3／10=9／10xl0／3=3(杯)，依据是什么呢?还是商不变性质，只是运用方式不同，将除数转化成整数1，也就是：9／10÷3／10=(9／10xl0／3)÷(3／10xl0／3)=3÷1=3(杯)。读懂了来龙去脉，在教学过程中就不是简单地讲授方法，可以引导学生在不同方法的尝试、比较、辨析中，从本质上掌握分数除以分数的计算方法。

第三，读教材的价值追求。以“加法交换律”为例，不仅要让学生知道什么是“加法交换律”，还可以此为载体渗透探究发现的学习方法和结构意识。因此教学过程主要有：

(1)生活现象：

借助一个现实情境或故事，比如成语故事“朝三暮四”引入，得到：3+4=4+3。

(2)引发猜想：

是不是只有3+4才等于4+3呢?其他两个数相加有没有这样的规律?

(3)举例验证：

你还能写出几个这样的等式来验证一下吗?可以独自完成，也可以小组合作。

学生举出很多例子，有一般数有特殊数；有一位数、两位数、三位数……；有整数、小数、甚至分数等等。

(4)归纳规律：

比较这些等式，它们有什么共同的地方?

引导学生归纳出“加法交换律”的内容，建立数学模型。

选用“现象—猜想—验证—归纳”的探究式学习方式，亮出了数学知识中最智慧的部分，作为实现数学学科育人价值的丰富资源，使学生在经历这些数学知识“再创造”的过程中，感受智慧、实践智慧、体现智慧。“猜想”能使学生了解知识的创生过程，激起学生对现象进行主动探究的欲望。以此为“引线”，可以让学生学会思考如何从偶然的现象中去发现必然的规律。学生一旦掌握了发现的一般方法，也就有了不断发现乃至创新的需要与可能。“验证”，让学生自己举例丰富了表象材料的积累，范围较广地进行“不完全归纳”。可见，教师的定位既有知识目标，还有学习方法的目标。这样让学生完整地经历了规律性知识的探究过程，充分地体验、发现和建构，逐渐形成善于主动地猜想与类比的习惯，促使学生的思维真正地主动投入。

二、立足主体——学生，孕育精彩课堂

1.读学生的学习需求

课程的实施都是以一定的学习内容作为载体的，作为老师，需要从儿童立场考察，学生为什么要学这个内容。怎样才能打动学生的心，激发起学生主动参与的热情呢?需要靠知识本身的魅力吸引学生。

《小数乘整数》：水果超市最近新进了两种水果，西瓜每千克0.8元。买3千克西瓜要多少元?0.8x3可以怎样算呢?如果就直接切入小数乘整数的计算方法，学生对此内容的学习缺乏兴趣，学习就变成了一种被动的应付，效率低下也就在情理之中。如果先让学生尝试解决，学生可能转化成小数加法用0.8+0.8+0.8=2，4(元)，也可能根据人民币单位问的进率把0.8元先化成8角，再用8角×3=24角。最后把24角化成2，4元，甚至有学生预习或者从其他途径知道还可以用0.8x3=2.4(元)。这些不同的方法都可以解决买3千克西瓜要多少元，但比较发现0.8x3=2.4(元)最简便，所以我们要学习它。为了学会这样的方法，从学生的角度看，他就有了理解算理的需求，只有算理清晰了，方法才会内化，才能正确应用。如果学生对知识本身产生了兴趣，那么他就会自觉主动地去探求知识。

2.读学生的学习状态

同一单元有不同课时的学习，学生的知识基础、能力储备以及活动的经验等，会随着学习状态的变化而变化。例如：“5的乘法口诀”的教学，在学习前，学生初步掌握了乘法计算的方法，口诀学习的过程，为本节课的学习迁移奠定了基础；在“1～4的乘法口诀”的学习时，学生经历了“选材料、写算式、编口诀、找规律”的过程，为本课学生主动学习提供了步骤过程的保障；在“1～4的乘法口诀”的学习中，学生不仅获得了乘法口诀的规律，同时体悟了发现规律的方法，为本课

规律获得提供了方法支撑。当然对上述结构的理解与掌握学生之间也会存在差异，这些都是课堂的资源。在对学生状态的深入分析和准确把握的基础上，我们需要思考递进性目标的设计。

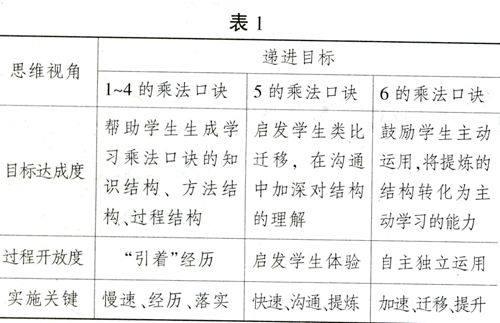
学生在类似内容的学习中有着不同的学习要求，似曾相识又有不同，基于已有，又需要“跳一跳”才能获得新知。学生有能力继续学习但又不是简单重复，不断提升的要求让学生始终处于学习的积极状态(见表1)。

3.读学生的年段特征

学生随着年龄的增长，知识逐步积累，能力逐步提升，经验逐渐丰富，因此，不同年段的学生对同类内容的学习方法、学习方式又有所不同。就“探究规律”而言，低年级学生以具体形象思维为主，他们发现规律，要从大量的材料中感知，如“余数小于除数”的规律，可以分组设计除数相同的几组算式，先研究除数是5的情况，通过具体的算式，让学生感知除数是5的算式有很多，但余数只有4种情况，所以除数是5，余数最大只能是4，进而得出余数要比除数小的猜想。然后引导学生计算除数是其他数的、有序排列的除法算式(如除数都是2的一组算式：2÷2，3÷2，4÷2，5÷2……20÷2；还有除数是3、4、6、7、8、9等数的几组算式)，验证猜想是否正确。四年级学生学习“乘法分配律”时，可以让学生运用前期规律探究的过程，自主经历“发现猜想、确定范围、举例验证、获得结论”，以学生的主动探究为主，教师的“引”和教师的举例相对于二年级学生要减少很多。

再如，《混合运算》“为什么先算乘后算加”的内在原理，在三年级让学生探究学生并不热心。但如果在五年级，学生热情相对会高，研究过程也会顺利一些。为什么会这样?我觉得主要原因就是学生年段特征。五年级学生的学习经验、学习能力有了积累，当教师提起这个问题时，他们也有一定的能力理解探究的意义和过程，所以一下来了兴致。探究过后，他们更多关注的是算理的内涵。可见同样的问题，不同年龄的学生对它的认知度、兴趣度是不一样的，初学计算时，学生也许对“为什么”的需求没有对“怎样做”来得强烈。学了一段时间，积累了一定的经验，站在更高的平台俯瞰时，追根究底的愿望会更强些。这要求我们更细致地研究每个学段学生的认知特点，设计适合他们的数学课堂。

美国著名作家弗格森曾说过这样一句话：每个人都守着一扇从内开合的改变之门，不论动之以情或晓之以理，我们都不能替别人打开这扇门。我们的数学教学也同样如此，确立儿童立场，从多维度、多层面关注学生真实的思维世界，并在此基础上想方设法地去推动学生的有效学习，提升学生的数学素养，才是真正有意义的教与学。

参考文献：

[1]成尚荣，儿童立场，教育从这儿出发[J]，人民教育，2007(23).