简单层次网络上的自组织临界行为

杨秋英，颜学文

（常熟理工学院物理与电子工程学院，江苏常熟 215500）

简单层次网络上的自组织临界行为

杨秋英，颜学文

（常熟理工学院物理与电子工程学院，江苏常熟 215500）

采用改进的二维格子地震（OFC）模型研究了简单两层网络上的雪崩行为.考虑到层间的性质或功能有差异，在OFC模型中引进层内控制参量α和层间控制参量β，得到其雪崩大小在一定范围内满足幂律分布，超出一定的值，系统便不再处于自组织临界态，而处于超临界态.另外，膜电位平均值的时间序列的功率谱也近似满足1/5幂律行为.

改进的OFC模型；层次网络；自组织临界行为

1 引言

自组织临界性（SOC）是Bak、Tang和Wiesenfeld在1987年提出来的[1]，主要指一大类有多个单元组成的复杂系统，在外界驱动和内部组元间的相互作用下，能够通过一个漫长的自组织过程演化到一个动力学临界状态.在这个状态下，系统的一个微小的扰动可能会通过类似“多米诺效应”的机制被放大，延伸到整个系统，形成大雪崩，其特征是雪崩大小分布遵从幂律分布.SOC理论可以用来解释很多复杂系统（例如地震系统[2]，生物演化系统[3]，经济系统[4]等）中出现的幂律行为.至1993年，相继提出了几个SOC模型[5-9]，其中之一是Olami、Feder和Christensen提出的OFC地震模型，他们在二维规则格点网络上模拟地震行为，并假设每个方向上的能量或力的传输是均等的.Hopfield[10]注意到脑的神经生物学中脉冲发放机制和地震模型中的累积-发放机制间有很强的相似性，他指出地震模型中的一个滑动事件对应神经细胞的一个动作电位，地层板块间的弹性连接对应于神经细胞间的突触连接，所以地震模型中的复杂行为在神经元中也可能存在，故可用累积-发放机制来模拟神经元的动力学行为.

实际神经元的连接表现出局部模块或群组织结构.神经元结构连接的信息表明哺乳动物脑皮层具有区域层次结构[11-12]，某些区域连接得紧密，而区域之间连接较稀疏.本文提出了一个简化的两层网络模型，层内运用最原始的二维规则网络，并将OFC动力学机制运用到两层层次网络上.这里考虑到网络是两层次的，层间的结构有所不同就有可能导致OFC模型中发放机制有所改变，我们用控制参量α和β分别来调节层内和层间的发放.下面详细讨论改进的OFC模型以及网络拓扑结构对自组织临界行为的影响.

2 模型

在我们的模型中采用两层规则网络，每层网格大小为S=30×30.两层网络之间的关系用边连接，为了简化，只取两网络中对应的节点进行连接，如图1所示，网络1中的节点4只和网络2中的节点4连接，而不与网络2中其他节点相连.

原初的OFC地震模型描述是在方格中任一节点都赋予一动力学变量Fi，在（0，1）之间取值，代表板块承受的应力，在神经元模型中，代表每个神经元的膜电位，再给出一阈值，取Fth=1，如果格子中所有格点的动力学变量Fi＜Fth时，认为地壳处于静息状态，为了描述地震应力的缓慢演化现象，增加所有地震的应力直到其中一个板块的应力超过阈值，板块变得不稳定，开始滑动.向邻近的节点发放应力，自己回落到静息态，即

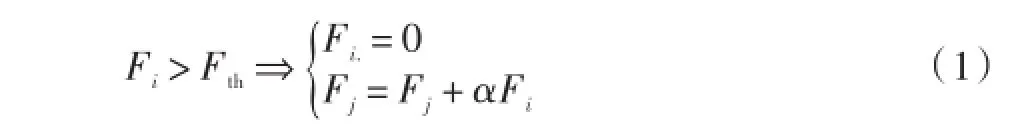
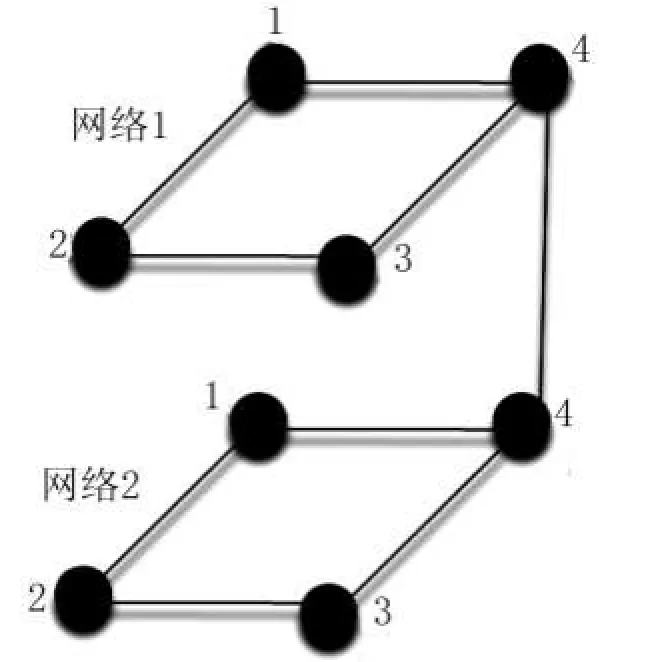
图1 层间节点的连接方式

式中j表示i节点的所有近邻，α是控制系统的动力学耗散水平的参量，当α=0.25时表示系统的能量守恒，α＜0.25对应能量耗散系统.

在同层次中发放满足：Fi→0，

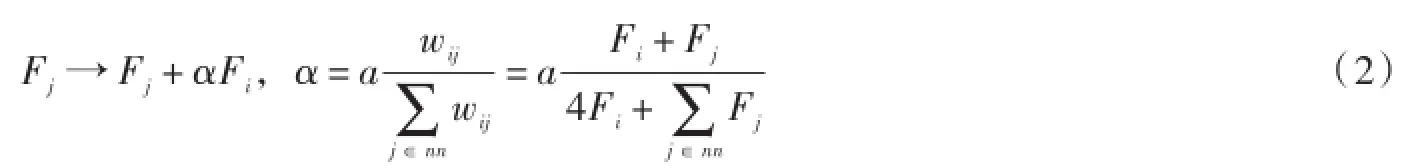
在不同层次间发放满足：Fi→0，

其中，wij表示i节点和j节点的动力学变量和，nn表示所有i节点的最近邻节点.这种发放模式一直进行直到网络中所有节点的变量Fi都小于阈值，即达到稳定状态，我们把这个过程定义为雪崩，而这过程中不稳定节点的总数定义为雪崩大小.

至此，我们已经完成了网络演化的动力学模型，下面具体研究在两层网络上的自组织临界行为.

3 模拟结果

3.1 雪崩大小概率分布

首先讨论雪崩大小的概率分布，即相同雪崩大小发生的概率.在我们的模型中，有多个可调参数：层间连接数、控制参量和网格大小等.

3.1.1 层间连接数对雪崩大小分布影响

首先研究不同层间连接数对雪崩大小分布的影响，选定其他参量：两层次网格大小N=1800，方程（2）（3）中的参量a,b都取为0.7，层间连接数取5，从图2可知，其一，雪崩大小分布不是一个简单的幂律分布，分布曲线中间出现拐点，行为相对复杂.其二，分布曲线尾部上翘，这一特征是超临界行为.由此可知层次之间应具有一定量的连接数，不然系统就处于超临界状态，便不能正常工作.

下面详细讨论层间不同的连接数对雪崩行为的影响.图3给出了相同参数条件下雪崩大小分布随层间连接数变化的关系，从图中可以看出，当连接数大于50时，忽略胖尾效应，雪崩大小分布满足幂律分布，即P(S)∝S-τ，随层间连接数增加幂律指数先增后减.另外，层间连接数为600时有个分界线.层间连接数小于600时，随连接数增加，分布的截断减小，即大雪崩减少；而大于600时，随着连接数增加，截断增加，即大雪崩增多.随着层间连接数的增加，雪崩大小分布出现了两种变化趋势.这是可以理解的，当层间连接数较小时，层次之间网格处于稀疏状态，关联度不高，此时增加连接数，只会导致每个节点被分配到的能量减少，不容易发生雪崩，而当连接数大到一定程度时，此时，层次间连接紧密，整个网络的连通性非常好，所以大雪崩越来越多.

在上面的研究中，我们给出了雪崩大小分布的统计性质，为更好地理解雪崩大小分布，下面给出整个网络的平均雪崩大小与层间连接数的关系，所谓平均雪崩大小，就是指这个网络达到稳定状态之前所有雪崩大小与所有雪崩次数的比值.图4给出了平均雪崩大小随层间连接数的变化关系（选定两层网格大小N=1800，控制参量a=0.7,b=0.7，层间连接数分别为100，200，500，600，700，850，900）.随着层间连接数增加，平均雪崩大小先减后增，这与雪崩大小分布的统计性质是一致的.

3.1.2 层间控制参量对雪崩大小分布的影响

当层间连接数很少时，系统行为趋于超临界态.我们选定层间连接数为50，研究层间控制参量对雪崩行为的影响.考虑到拓扑结构的不同，层内和层间网络的动力学行为应有所不同，我们来考察层间控制参量对雪崩大小分布的影响.选层内动力学行为的控制参量a固定为0.7，改变层间动力学行为的控制参量b.从图5中得到，当b＞0.7时，雪崩大小分布满足幂律行为，且随b增大，截断反而减小.而当b＜0.7时，尾部同样出现了上翘现象，这是超临界特征.

3.1.3 网格大小对雪崩大小分布的影响

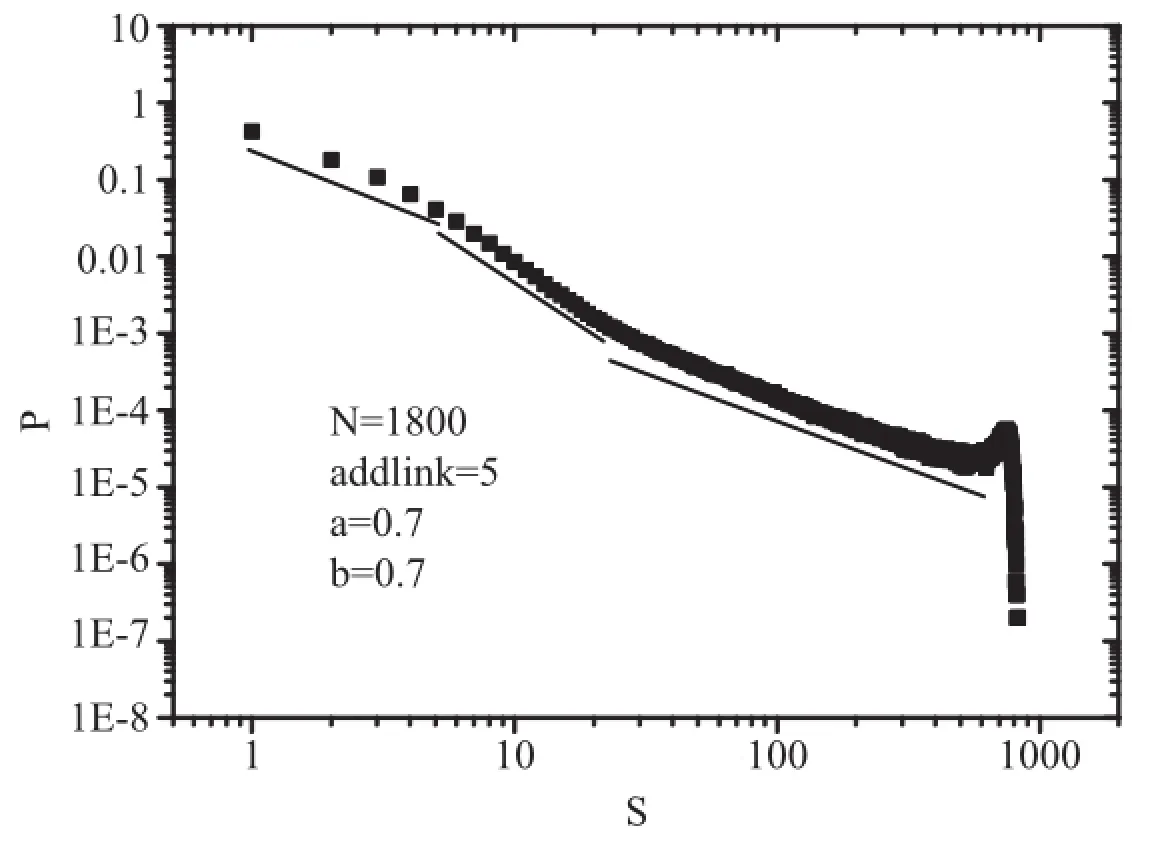
图2 层间连接数为5时雪崩大小分布图

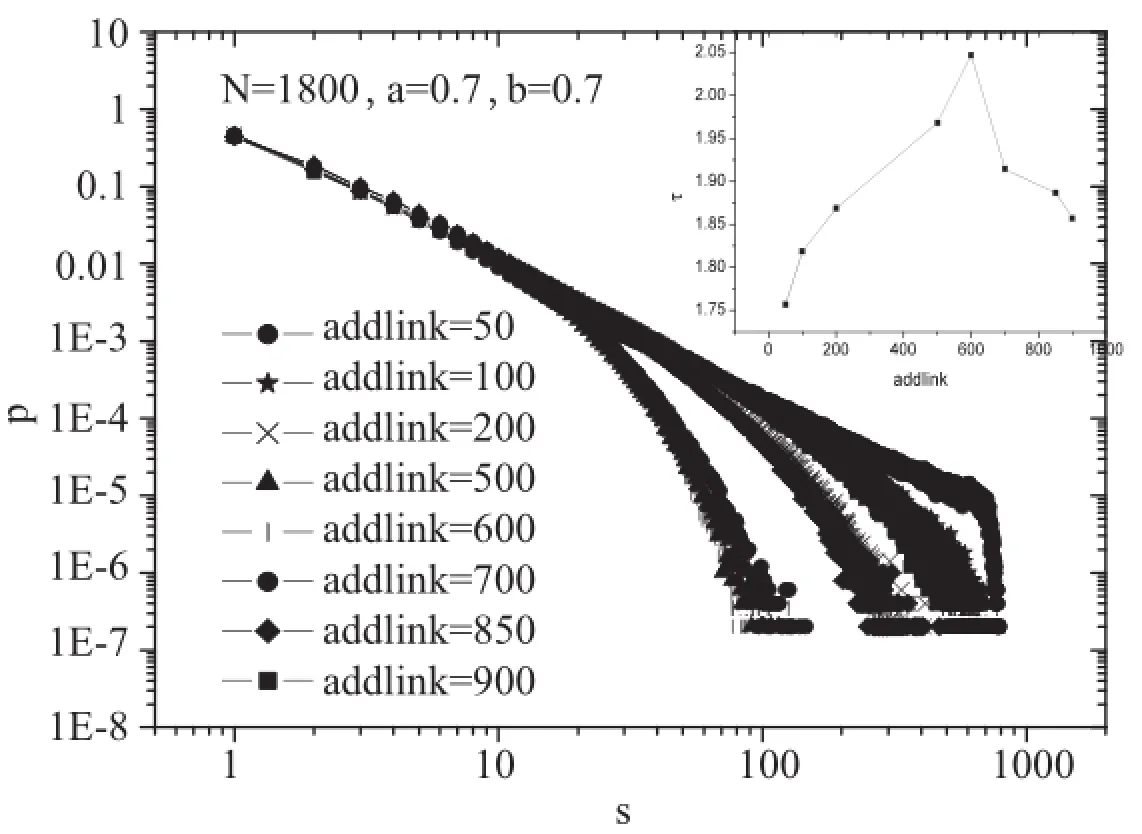
图3 不同层间连接数对应的雪崩大小分布图，插图是幂指数随连接数变化的关系图

图4 不同层间连接数对应的平均雪崩大小

选定控制参量a=0.7,b=0.7，单层二维网格大小为L×L，L分别取32，48，64.研究雪崩大小分布情况.图6中左边是雪崩大小分布的原始数据图，可以看到除去胖尾，雪崩大小分布满足幂律分布，并随网格增大，大雪崩出现的概率增大.为了提取胖尾中的噪音信息，图6右边对雪崩大小分布做了分箱统计[17].从图中可以看出，分箱统计方法有效减少了大规模雪崩的噪音影响，使模拟效果更接近真实情况.

3.2 类脑电波及功率谱分析

下面研究大脑中神经元膜电位的暂态性质.不同时间所有神经元膜电位的平均值，即一个时间序列信号，由于它的波形与脑电波相似，故称为类脑电波.我们把每次雪崩完成后，所有节点膜电位平均值的时间序列定义为

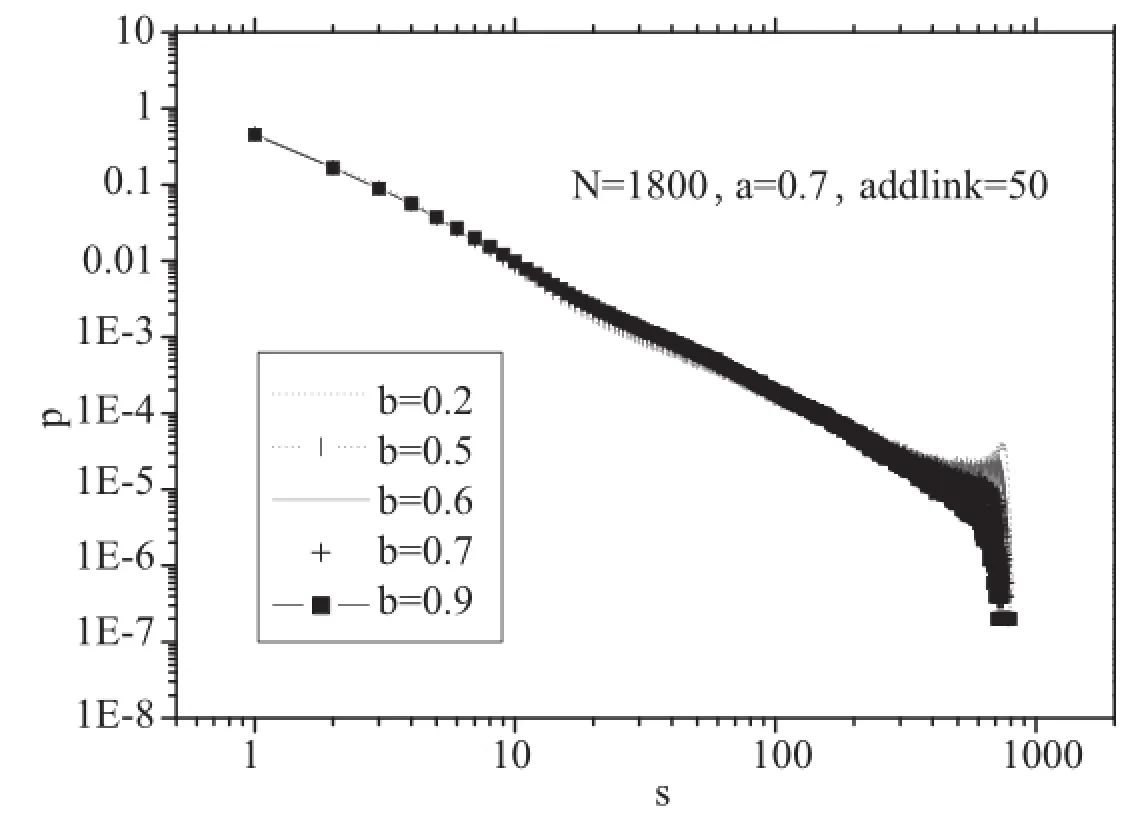
图5 层间控制参量对应的雪崩大小分布图

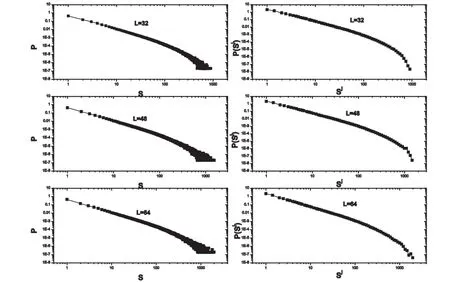
图6 左为不同网格大小对应的雪崩大小分布图，右为对原始数据作分箱统计后的雪崩大小分布图

类脑电波，数学表达式为：

由于整个模拟数据太大，图形表示不清晰，故从中选取时间步从2000到4000步，其时间序列如图7（a）所示，平均膜电位在某个值附近振荡.同时我们还对这个平均膜电位信号做了功率谱分析，如图7（b）所示，它满足1 f的幂律分布，这也是通常所说的1 f噪声.选定两层网格大小N=1800，层间连接数为100，控制参量a=1,b=0.8，其类脑电波的功率谱满足S(f)∝f-τ，幂律指数τ=1.7948，验证了大脑处于一个自组织临界态.

图7 （a）平均膜电位的时间序列图，（b）平均膜电位的时间序列的功率谱

4 结论

为了体现神经元的团簇性，我们在拓扑结构中采用了两层规则网络，同时考虑到节点的发放与邻近神经元有关，在原初的OFC模型中加入了与邻近节点相关的权重值.研究发现，该模型在一定范围内体现SOC行为.即雪崩大小分布满足幂律分布.但是当模型中的参量超出一定范围时，则出现由自组织临界到超临界状态的转变.此外，还研究了在一定参量值时的类脑电波，发现其功率谱也满足幂律性质，说明大脑工作状态处于自组织临界态.

[1]Bak P,Tang C,Wiesenfield K.Self-organized criticality:An explanation of the 1/f noise[J].Phys Rev Lett,1987,59(4):381-384.

[2]Gutenberg B,Richter C F.Magnitude and energy of earthquakes[J].Ann Geofis,1956,9:1-15.

[3]Raup M D.The nemesis affair：a story of the death of dinosaurs and the ways of science[J].Science，1986，251：1530.

[4]伯努瓦·B·曼得布罗特.大自然的分形几何[M].陈守吉，凌复华，译.上海：上海远东出版社，1998.

[5]Tang C,Bak P.Critical exponents and scaling relations for self-organized critical phenomena[J].Phys Rev Lett,1988,60(23): 2347-2350.

[6]Burridge R,Knopoff L.Model and theoretical seismicity[J].Bull Seismol Soc Am,1967,57:341-371.

[7]Olami Z,Feder S,Christensen K.Self-organized criticality in a continuous,nonconservative cellular automaton modeling earthquakes[J].Phys Rev Lett,1992,68(8):1244-1247.

[8]Christense K,Olami Z.Scaling,phasetransitions and nonuniversality in a self-organized critical cellular-automaton model[J].Phys Rev A,1992,46(4):1829-1838.

[9]Bak P,Sneppen K.Punctuated equilibrium and criticality in a simple model of evolution[J].Phys Rev Lett,1993,71:4083-4086.

[10]Hopfield John J.Neurons,dynamics and computation[J].Physics Today,1994,47(2):40.

[11]Stephan K E,Kamper L,Bozkurt A,et al.Advanced database methology for the collation of connectivity data on the macaque brain (CoCoMac)[J].Phil Trans R Soc Lond B Biol Sci,2001,356:1159-1186.

[12]Scannell J W,Blackmore C,Young M P.Analysis of connectivity in the cat cerebral cortex[J].J Neurosci,1995,15:1463-1483.

[13]Li Wenyuan,Lin Yongjing,Liu Ying.The structure of weighted small-world networks[J].Physica A:Statistical Mechanics and its Applications,2007,376:708-718.

[14]Lu Xin Biao,Wang Xiao Fan,Li Xiang,et al.Synchronization in weighted complex networks:Heterogeneity and synchronizability [J].Physica A:Statistical Mechanics and its Applications,2006,370(2):381-389.

[15]Zhang G Q,Tirnakli U,Wang L,et al.Self organized criticality in a modified Olami-Feder-Christensen model[J].Eur Phys J B, 2011,82(1):83-89.

[16]Yamamoto T,Yoshino H,Kawamura H.Simulation study of the inhomogeneous Olami-Feder-Christensen model of earthquakes [J].Eur Phy J B,2010,77:559-564.

[17]Christensen K,Moloney N R.Complexity and Criticality[M].England,London:Imperial college press,2005.

SOC Behavior of Simple Hierarchical Network

YANG Qiu-ying,YAN Xue-wen
(School of Physics and Electronics Engineering,Changshu Institute of Technology,Changshu 215500,China)

The avalanche behavior of simple two-level network is studied by using the improved OFC model in this paper.Considering the different nature or function between levels,two different control parameters,andare introduced to express control parameters of level internal and levels respectively.The conclusion is reached that the avalanche distribution obeys the power-law distribution within a certain range.The system will not be in the self-organized critical state,but in the supercritical state when the parameters exceed the certain value.Otherwise, the power spectrum of time series of the average membrane potential approximately obeys the power-law behavior.

improved OFC model;hierarchical network;self-organized critical

N93

B

1008-2794（2012）04-0046-06

2012-03-10

杨秋英（1981—），女，江苏常熟人，讲师，硕士，研究方向：复杂网络及非线性动力学.