一个猜想的微分法证明及推广

薛惠良，汤炳兴

（1.常熟市中学，江苏常熟 215500；2.常熟理工学院数学与统计学院，江苏常熟 215500）

一个猜想的微分法证明及推广

薛惠良1，汤炳兴2

（1.常熟市中学，江苏常熟 215500；2.常熟理工学院数学与统计学院，江苏常熟 215500）

利用排序不等式证明猜想（1）的轮换对称不等式（2）；把所给出的命题建模为二元函数，使用二元函数极值的判定定理给出猜想的证明；同时把猜想中的指数从正整数k推广到了实数R+；当k=1时，对称式（2）就是著名的内斯比特不等式的推广.最后把猜想（1）推广到更一般的情形，得到命题③和④.

轮换对称；排序不等式；偏微分；极值定理；内斯比特不等式；推广

1 引言

《数学通报》2009年10月第1818号数学问题如下：

设a,b,c∈R+,试证：

文献[1]把1818号问题作了等价变形，并给出了命题：a,b,c∈R+,k∈N,k≥2

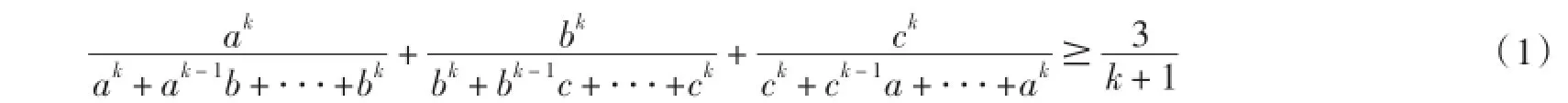
不等式（1）当k=2,3,4,6时成立，并猜想k对于任意不小于2的整数均成立.

2 主要结果

首先证明（1）的轮换对称式：a,b,c∈R+,k∈N,k≥2

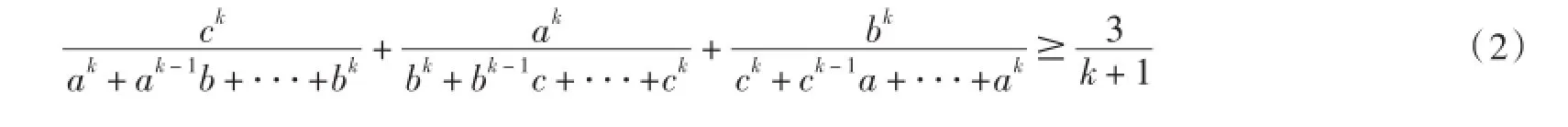
成立.

其次用微分法证明当k＞1，（k∈R）时（1）式成立，当0＜k＜1，（k∈R）时（1）式的不等号反向成立；再探究当k=1时（1）式不成立及（2）式成立的背景.

2.1 不等式（2）的证明

故命题②成立.

2.2.2 在A最值存在条件下，用初等方法探究A的最小值

设a,b,c∈R+,k∈N,k≥2，

样就有

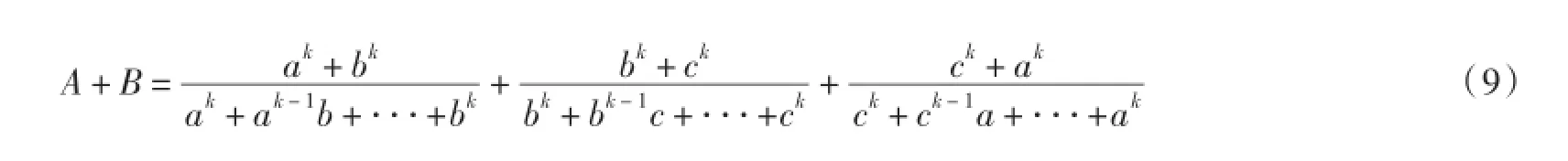
的最小值为2t.

由（3）、（4）、（5）、（9）得

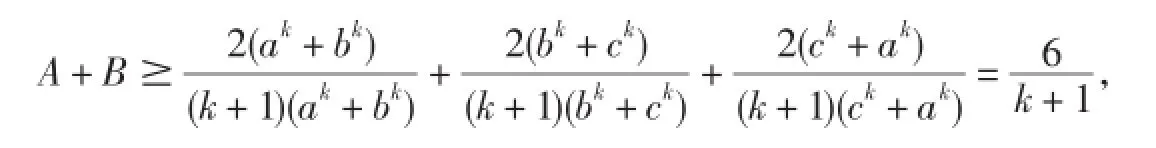
当且仅当a=b=c时等号成立.

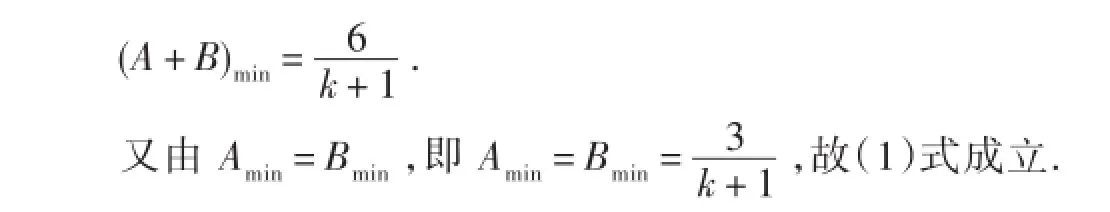
2.3 探究当k=1时不等式（1）与（2）的成立与否

当k=1时不等式（2）显然成立，即a,b,c∈R+,则有

（10）式显然是内斯比特不等式.事实上，当a,b,c∈R+时，由柯西不等式得

故不等式（1）不能成立.

对于k元一次齐次式，我们有：若ai∈R+,i=1,2,⋅⋅⋅,k，k∈N,k≥2,则

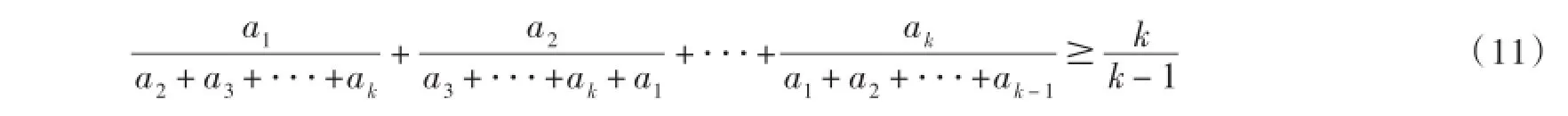
不等式（11）是内斯比特不等式的推广.

2.4 不等式（1）的推广

命题③若ai∈R+,i=1,2,⋅⋅⋅n,k∈R,k＞1，则有，

用命题②③的证明过程，容易得到命题④的证明.

[1]蔡祖才.数学问题1818的等价式推广[J].数学通报，2010（12）：58．

[2]常庚哲，史济怀.数学分析教程[M].北京：高等教育出版社，2003．

Proof and Generalization of a Method of Differentiation Hypothesis

XUE Hui-liang1,TANG Bing-xing2
(1.Changshu Middle School,Changshu 215500,China; 2.School of Mathematics and Statistics,Changshu Institute of Technology,Changshu 215500,China)

Sorting algorithm and inequality is used to testify rotation symmetric inequality(2)of hypothesis(1);the propositions are utilized to model binary function,and the laws of two variable extreme value are used to prove the hypothesis.Meanwhile,the hypothesis spreads exponents from positive integer K to real number R+;When K=1, symmetric expression(2)is the spread of Nesbitt’s inequality.In the end,hypothesis(1)can be generalized to more common conditions,thus concluding proposition③and proposition④.

rotational symmetry;sorting algorithm and inequality;partial differential;laws of two variable extreme value;Nesbitt’s inequality;generalization

0172.1

A

1008-2794（2012）04-0041-05

2012-01-08

薛惠良（1957—），男，江苏常熟人，江苏省常熟市中学高级教师.