一类分数阶微分方程系统边值问题正解的存在性

申腾飞，宋文耀

（中国矿业大学理学院，江苏徐州 221008）

一类分数阶微分方程系统边值问题正解的存在性

申腾飞，宋文耀

（中国矿业大学理学院，江苏徐州 221008）

利用锥拉伸与压缩不动点定理和Leray-Schauder非线性抉择，讨论了一类非线性的Riemann-Liouville分数阶微分方程耦合系统边值问题，得出边值问题的正解存在的充分条件.

分数阶微分方程；边值问题；不动点定理；正解

近年来，分数阶导数及分数阶微分方程在科学、工程和数学等领域得到了重要应用，例如已成功应用于粘弹性材料、信号处理、控制、生物等领域[1].许多学者投入到分数阶微分方程的研究，并取得了很多研究成果[2-12].

苏新卫用Schauder不动点定理研究一类分数阶微分方程耦合系统边值问题

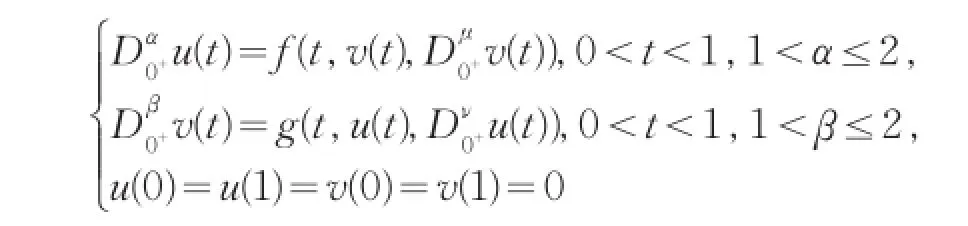
正解的存在性[2]；白占兵，吕海深[3]研究了一类分数阶微分方程两点边值问题，Bashir Ahmad[4]讨论了一类三点的分数阶微分方程耦合系统边值问题.本文将采用锥拉伸与压缩不动点定理和Leray-Schauder非线性抉择研究下面的一类分数阶微分方程耦合边值问题.

本文主要讨论以下分数阶3＜α,β≤4的微分方程系统的边值问题

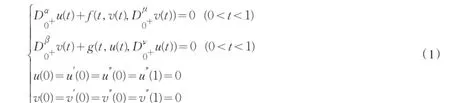
正解的存在性，其中

f,g:[0,1]×R+×R→R+连续函数，利用Leray-Schauder非线性抉择，锥上不动点定理，给出该问题的至少存在正解的充分条件.

1 预备知识

定义1[3]函数y:(0,+∞)→R的α阶Riemann-Liouville分数阶积分为

其中，α＞0，Γ(⋅)为gamma函数.

定义2[3]连续函数(0,+∞)→R的α阶Riemann-Liouville分数阶导数为

其中，α＞0，Γ(⋅)为gamma函数，n=[α]+1.

引理1[3]若α＞0，u∈C(0,1)⋂L(0,1),则分数阶微分方程u(t)=0有唯一解

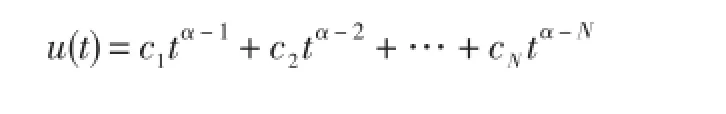
其中N为大于或等于α的最小整数.

引理2[3]若α＞0，u∈C(0,1)⋂L(0,1)，u∈C(0,1)⋂L(0,1)，则存在ci∈R,i=1,2⋅⋅⋅,N，使得

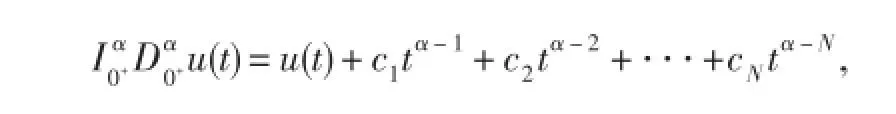
其中N为大于或等于α的最小整数.

引理3若y(t)∈C[0,1]且3＜α≤4,则分数阶微分方程

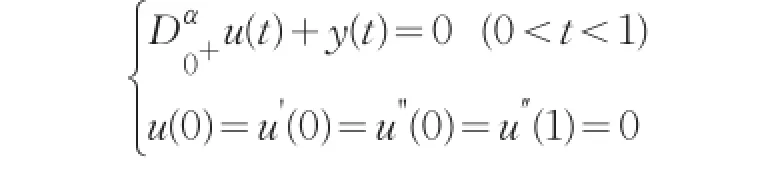
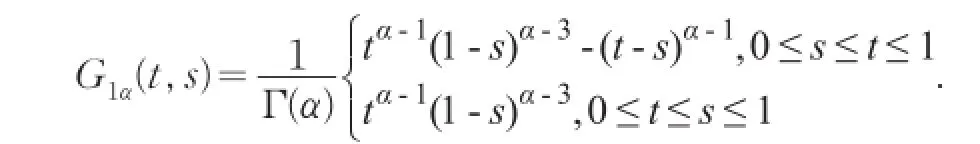
证明由引理2，存在ci∈R,i=1,2,3,4,使得分数阶微分方程的解等价于

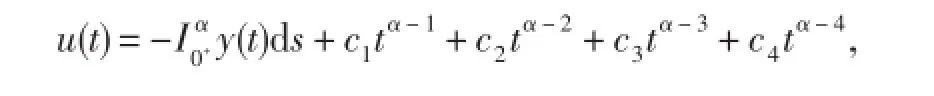
其中c1,c2,c3,c4是待定常数,

即

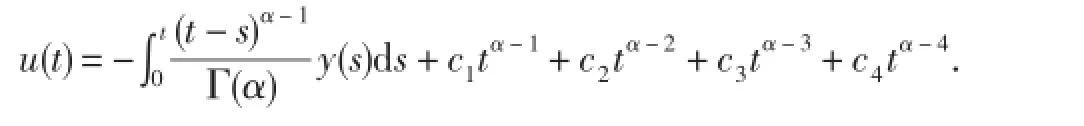
由边值条件u(0)=0可得c4=0.

所以

由u'(0)=0可得c3=0.

所以

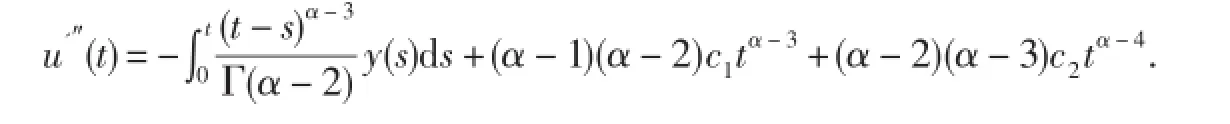
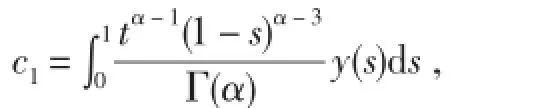
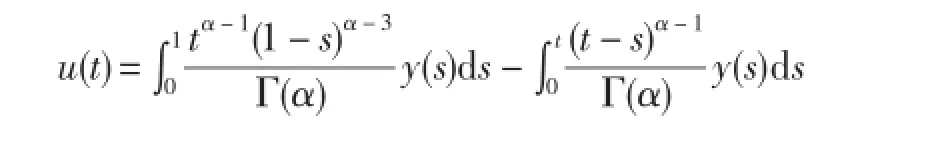
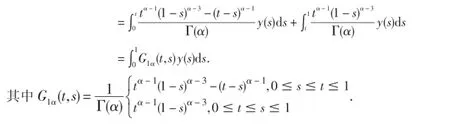
引理4G1α(t,s)有下面的性质：

故G(t,s)≥0.

当t≤s时，显然G(t,s)≥0.

（2）根据G(t,s)的定义式，对于给定s∈(0,1)，G(t,s)在定义区间上关于t是增函数，则G(t,s)≤G(1,s).

当s≤t时，

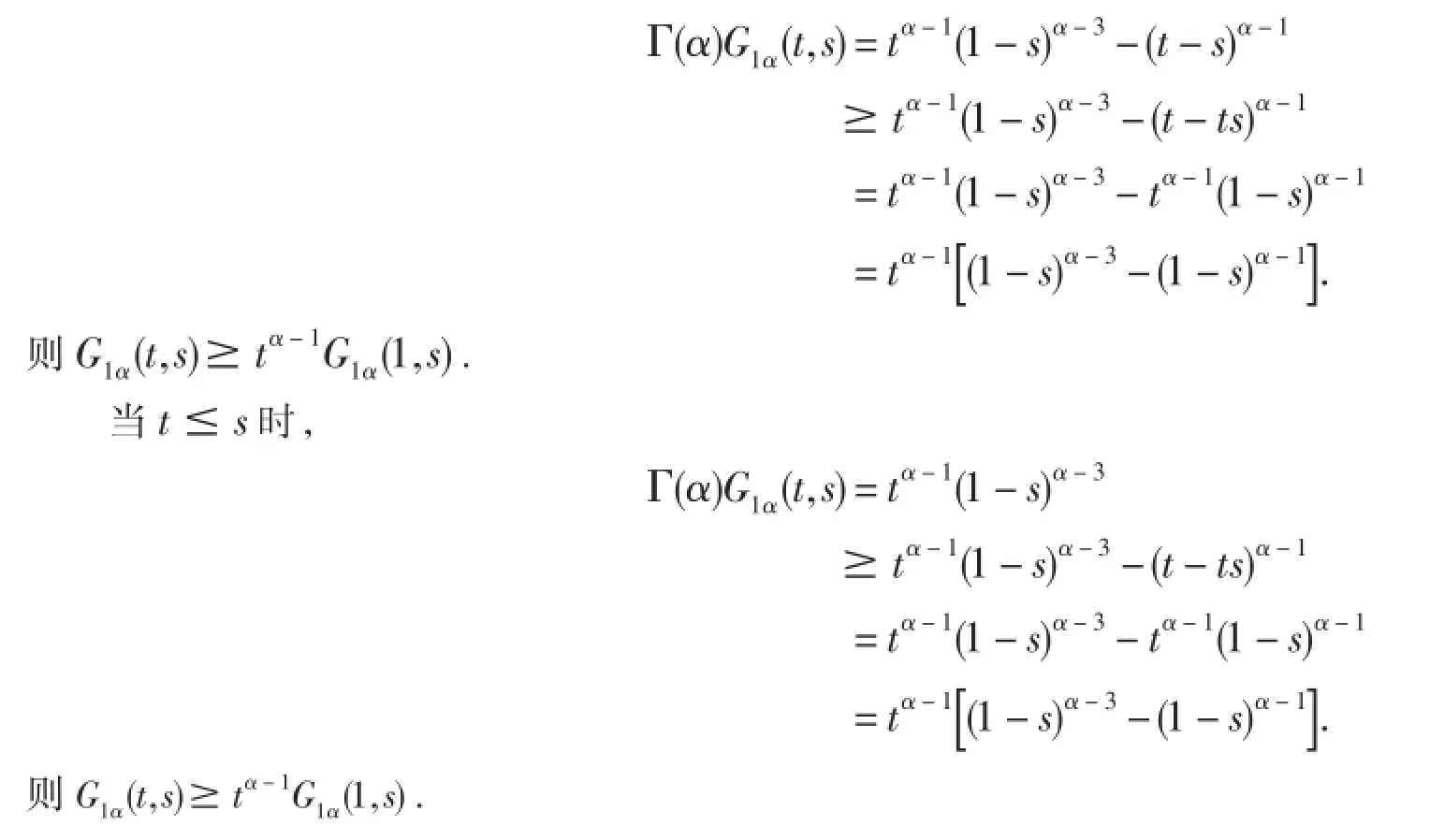
引理5G1α(t,s)有下面的性质：

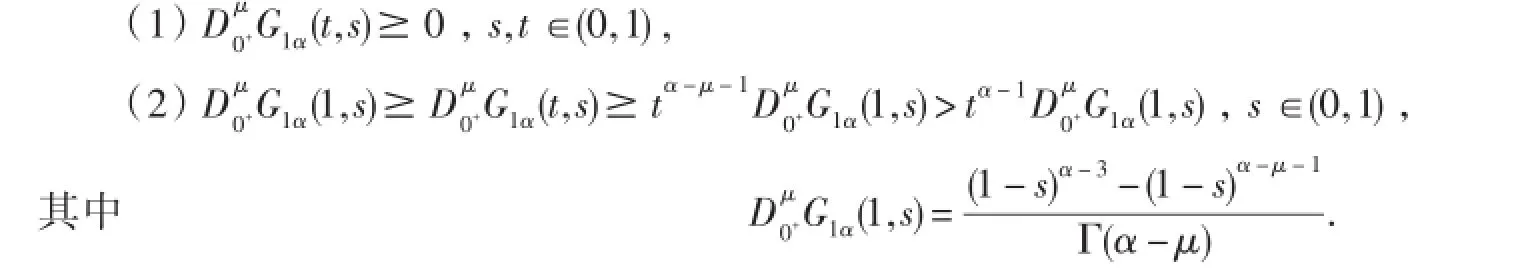
证明证明过程类似引理4，在此省略.

考虑积分方程系统

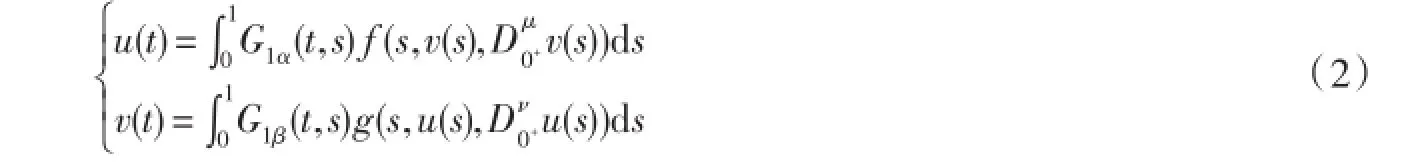
引理6[2]若f,g:I×R+×R→R+连续函数，则(u,v)是系统（1）的解当且仅当它是系统（2）的解.

引理7[12]设X是Banach空间，P⊂X是X中的锥，设Ω1,Ω2为X中的有界开集且为一全连续算子，若满足下列条件之一：

引理8[12]（Leray-Schauder非线性抉择）设K是Banach空间X的闭凸集，Ω为K中的相对开集，0∈Ω且T)是有界的，T:→K全连续，则

（2）存在一个点u∈∂Ω和λ∈(0,1)，使得u=λTu.

2 主要结果

下面证T(P)⊂P是一致有界的.

设Ω是P的有界集，则存在A1,A2＞0，使得‖v‖vX≤A1，‖u‖X≤A2，对于∀v,u∈Ω，

令

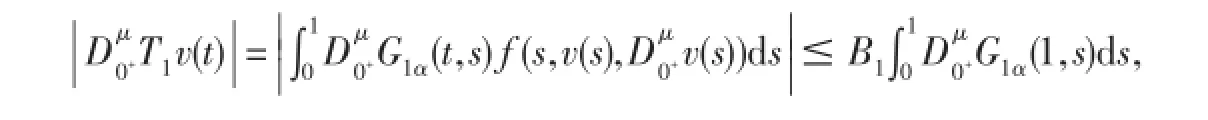
故‖T1vX‖是一致有界的.

再证T是等度连续的.

故T1是等度连续的，同理可证T2是等度连续的，因此T是等度连续的，由Arzela-A sc oli定理知T(P)是相对列紧的，故T是全连续的.

为了叙述方便，我们定义如下常数：

定理1设f,g:I×R+×R→R+上的连续函数，若存在两个正常数l2＞l1＞0，使得

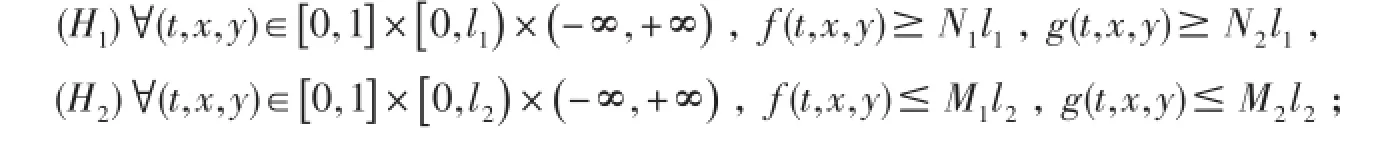
则问题（1）存在一个正解.

证明令Ω1={(u,v):‖u‖＜l1,‖v‖＜l1}，则0＜u(t),v(t)＜l1，∀t∈I.

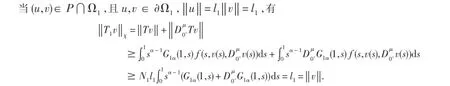
因此，当v∈P⋂Ω1时有‖T1v‖≥‖v‖.

同理可得：当u∈P⋂Ω1时‖T2u‖≥‖u‖.故‖T(u,v)‖≥l1=‖(u,v)‖.

另一方面，令Ω2={(u,v):‖u‖＜l2,‖v‖＜l2}，则0＜u(t),v(t)＜l2，∀t∈I.

当(u,v)∈P⋂Ω2，且u,v∈∂Ω2，‖u‖=l2，‖v‖=l2，有

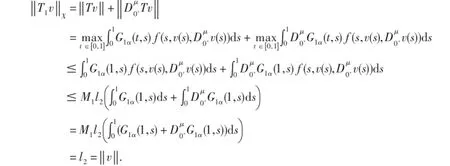
则方程（1）有一个正解.

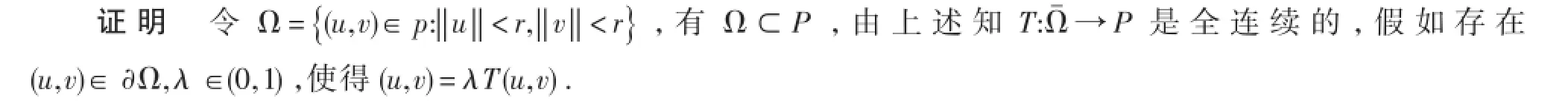
由已知条件，对于∀t∈[0,1]，我们有

[1]Kilbas A A,Srivastava H M,Trujillo J J.Theory and Applications of Fractional Differential Equations[M].Amsterdam：Elsevier, 2006.

[2]Xinwei Su.Boundary value problem for a coupled system of nonlinear fractional differential equations[J].Appl Math Lett,2009,22：64-69.

[3]Zhanbing Bai,Haishen Lv.Positive solutions for boundary value problem of nonlinear fractional differential equation[J].J Math Anal Appl,2005,311(2):495-505.

[4]Bashir Ahmad,Juan J Nieto.Existence results for a coupled system of nonlinear fractional differential equations with three-point boundary conditions[J].Comput Math Appl,2009,58:1838-1843.

[5]Hongrui Sun,Lutian Tang,Yinghai Wang.Eigenvalue problem for p-Laplacain three-point boundary value problems on time scales [J].J Math Anal Appl,2007,331:248-262.

[6]Shuqin Zhang.Positive solutions for boundary value problems of nonlinear fractional differential equations[J].Electronic Journal of Differential Equations,2006(36):1-12.

[7]Gan S Q.Dissipativity of θ-methods for Nonlinear Volterra Delay-integro-differential Equations[J].J Comput Appl Math,2007, 206:98－907.

[8]Shuqin Zhang.Existence of positive solution for some class of nonlinear fractional differential equations[J].J Math Anal Appl,2003, 278:136-148.

[9]Xiaojie Xu,Daqing Jang.Multiple positive solutions for the boundary value Problem of a nonlinear fractional differential equation[J]. Nonlinear Analysis,2009,71:4676-4688.

[10]Zhanbing Bai.On positive solutions of a nonlocal fractional boundary value problem[J].Nonlinear Analysis,2010,72：916-924.

[11]苏新卫.分数阶微分方程耦合系统边值问题解的存在性[J].工程数学学报，2009，26（1）:133-137.

[12]葛渭高.非线性常微分方程边值问题[M].北京：科学出版社，2007.

Existence of Positive Solutions for Boundary Value Problem of a Coupled System of Nonlinear Fractional Differential Equations

SHEN Teng-fei,SONG Wen-yao
(College of Science,China University of Mining&Technology,Xuzhou 221008,China)

In this paper,the existence of positive solutions for boundary value problem of a coupled system of non⁃linear fractional differential equations was discussed.By using the fixed-point theorems,some results were ob⁃tained.

fractional differential equation;boundary value problem;fixed point theorem;positive solution

O175.8

A

1008-2794（2012）04-0028-07

2012-03-31

申腾飞（1987—），男，安徽蚌埠人，中国矿业大学应用数学专业研究生，研究方向：微分方程.