基于自适应卡尔曼算法的重型半挂车状态估计研究*

2012-04-18张不扬宗长富王化吉郑宏宇

汽车技术 2012年7期

张不扬宗长富王化吉郑宏宇

（吉林大学汽车仿真与控制国家重点实验室）

1 前言

重型半挂车主动安全控制常用的估计算法包括卡尔曼滤波法、龙贝格观测器、鲁棒观测器、滑模观测器、模糊观测器、非线性观测器和神经网络算法等。其中，经典卡尔曼滤波算法最为常用[1]，但其只适用于线性系统。文献[2]和文献[3]中通过扩展卡尔曼滤波进行了行驶状态估计，文献[4]中使用双无轨卡尔曼滤波计算车辆状态及路面附着系数。这些滤波算法虽然解决了非线性系统的问题，但仍存在滤波器性能下降、难以适应复杂的环境变化及受观测噪声统计特性影响较大[5]等缺点。针对上述问题，一些学者提出了自适应卡尔曼滤波算法，该方法能够不断计算、更换噪声协方差，增强算法准确性[6，7]。

针对重型半挂车的横摆和折叠两种常见稳定性问题，建立了用于估算横摆角速度和半挂车折叠角的半挂车三轴简化动力学模型，并用商业软件Trucksim对简化模型进行了验证。

2 重型半挂车三轴简化动力学模型

本文用来估算模型横摆角速度和折叠角的动力学模型是重型半挂车三轴简化动力学模型，该模型以前轮转角作为输入，模型假设如下：

a. 牵引车速度与挂车速度相等且恒定；

b. 忽略车辆的俯仰运动；

c. 忽略空气阻力作用；

d. 忽略轮胎特性随负载不同发生的变化；

e. 忽略轮胎回正力矩作用。

重型半挂车三轴简化动力学模型如图1所示，其中，r1、r2分别为牵引车和挂车的横摆角速度，定义逆时针方向为其正方向，则r1、r2可表示为：

由于所用模型假设转角输入较小，则牵引车质心处的侧向加速度为：

重型汽车模型车轮侧偏角可由公式（5）～公式（7）得到：

整车的侧向力平衡方程如下：

（m1+m2）（v˙+ur）－m2（c+d）r˙－m2dq˙

牵引车质心处力矩平衡方程为：

铰接点处得到的挂车力矩平衡方程如下：

公式中，m1为牵引车质量；m2为半挂车质量；J1为牵引车转动惯量；J2为半挂车转动惯量；γ为牵引车与半挂车的铰接角；q为铰接角速度；q˙为铰接角加速度；u为牵引车纵向速度；v为侧向速度；ψ为牵引车横摆角；a为牵引车转向轴到质心的距离；b为牵引车驱动轴到质心距离；c为铰接点到牵引车质心的距离；d为铰接点到半挂车质心的距离；e为半挂车车轴到半挂车质心的距离；C1、C2、C3分别为车辆三轴车轮轮胎侧偏刚度。

令x=[v r q γ]T，将上述微分方程整理成状态空间形式：

模型建立后，借助Trucksim软件进行模型验证，在车速为60 km/h扫频工况下，动力学模型输出与Trucksim仿真结果对比如图2和图3所示，可见此模型能够描述车辆的横摆运动。

3 自适应卡尔曼滤波算法

系统状态方程与观测方程为：

式中，x（k）与 x（k+1）为 k 与 k+1 时刻的状态矢量；y（k+1）为 k+1 时刻的观测矢量；V（k+1）为 k+1 时刻的观测噪声；H为观测矩阵，H=[0 1 0 0]；W为系统噪声。

自适应卡尔曼滤波算法分为3部分，即在原有的时间更新和测量更新中加入了具有自适应性的自适应更新部分。

a.滤波时间更新部分

状态预测方程：

误差协方差预测：

式中，G=M－1A；T=M－1B；ε 是中间变量；b 为 0～1 之间的数值，为遗忘因子，能够限制滤波的记忆长度。

b.滤波测量更新部分

增益方程：

滤波方程：

误差协方差更新：

c. 滤波自适应更新部分噪声均值、自协方差矩阵估计计算：

4 仿真结果分析

本文采用Trucksim中的半挂车模型运算数据与自适应卡尔曼滤波算法估计值进行对比，以验证自适应卡尔曼滤波算法的有效性。自适应卡尔曼滤波状态估计流程如图4所示。车辆模型参数如表1和表2所列。车速分别为30 km/h与60 km/h，正弦扫频转向输入工况如图5、图6所示。由自适应卡尔曼滤波估计得到车速为30 km/h与60 km/h扫频工况下的横摆角速度、铰接角与Trucksim仿真得到的横摆角速度、铰接角对比曲线分别如图7～图9、图10～图12所示。

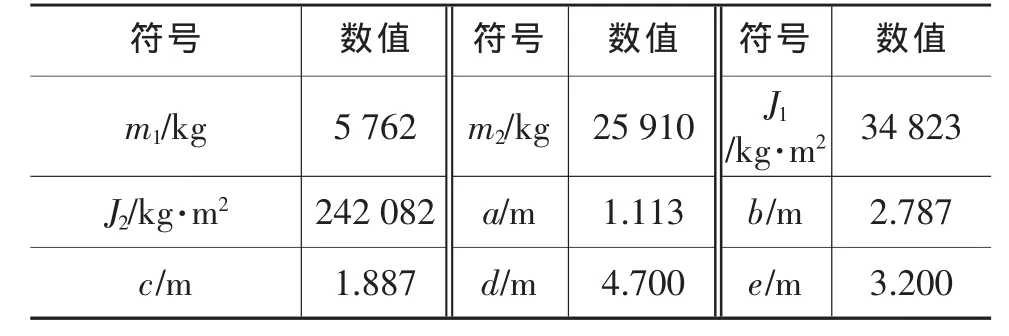
表1 车辆模型参数

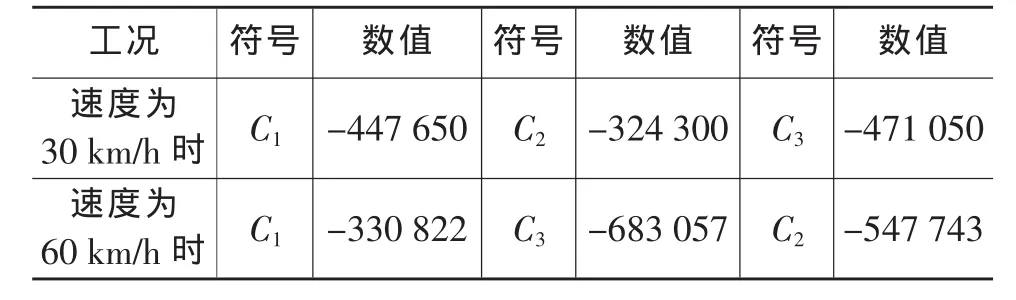
表2 车轮侧偏刚度（rad）－1

由图7～图9可以看出，30 km/h扫频工况下的系统估计结果输出重合度很高。图12显示，尽管60 km/h扫频工况下估计结果出现了误差，但与仿真结果趋势一致，满足估计要求。误差的出现是由本文所建立重型半挂车三轴简化动力学模型造成，即模型在低速非线性工况下能够较好的描述车辆的实际运动状况，但在高速非线性工况下，模型的输出结果与车辆的实际状况有一定差别。通过所设计的状态估计器，结合该模型对车辆高速非线性工况时的状态估计，虽然仍旧存在一定偏差，但是误差结果在可接受范围内，满足估计精度要求。