鹤壁市旱地小麦土壤养分与产量的数学模型研究

徐令超，王占中，刘振东，梅兹君，郭瑞林

(1.鹤壁市农业科学院，河南鹤壁458000;2.安阳工学院，河南安阳455000)

目前，中国小麦配方施肥技术研究大多采用农业部《测土配方施肥技术规范(试行)修订稿》中推荐的“3414”肥料效应试验方案［1，2］.该方案既吸收了回归最优设计处理少，效率高的优点，又符合肥料试验和施肥决策的专业要求.因此，这种设计与方案备受研究者青睐，在指导中国小麦配方施肥研究和应用过程中发挥了重要作用［3，4］.然而，在具体研究实施过程中发现，在采用这种设计方案建立数学模型时，大多研究者都是从施肥量的角度出发，来探讨肥料与产量之间的关系，从而确定最佳施肥方案的［5，6］.为此，本研究以土壤养分(基本肥力)为自变量因素，建立了小麦产量与土壤全氮、速效磷、有机质之间的数学模型，以便为指导鹤壁市旱地小麦大面积生产提供科学依据.

1 材料与方法

试验在鹤壁市郊区丘陵旱地进行.供试土壤为褐土类，中壤土.小麦品种为豫麦2号.根据小麦的种植情况和试验要求，在鹤壁市郊区三乡一镇丘陵旱地布置43个有代表性的取样点.取样点品种、气候、土壤类型、栽培管理措施基本一致.于小麦收获季节在大田生长均匀一致，代表性强的田块收获10 m2小麦植株，脱粒称重，折算亩产;同时在1 m2内用土钻多点取土壤样品，取土深度20 cm.

采用半微量凯式定氮法测定全氮，采用钼锑钪比色法测定速效磷，采用重铬酸钾容量法(外加热法)测定有机质含量.所获产量与化验分析测定结果一一对应，作为建模的样本原始数据.

采用三元三次曲线模型拟合产量与土壤养分之间的关系［7］.数学模型为:

Y=b0+b11N+b12N2+b13N3+b21P+b22P2+b31M+b32M2+b11×21NP+b11×31NM+b21×31PM

式中:Y表示产量，b表示回归系数，N表示土壤全氮含量，P表示土壤速效磷含量，M表示有机质含量.

2 结果与分析

2.1 土壤养分与小麦产量关系分析

将43个样点原始数据进行整理，剔除异常数据之后，剩余35个样点，结果如表1所示.

最高产量出现在第12个样点，666.7 m2产量达376.5 kg，最低产量出现在第 30 个样点，666.7 m2产量为230.0 kg，较最高产量低 146.5 kg.35 个样点平均666.7 m2产量为 288.84 kg.有18个样点的产量低于平均产量，占总样点的51.4%，说明鹤壁市旱地小麦增产的潜力还很大.

表1 土壤养分及小麦产量测定结果Table 1 Measured results of wheat yield and soil nutrients

续表Continuing table

2.2 土壤养分的空间变异

土壤养分的空间变异以速效磷为最大，变异系数为72.77%，属强变异，说明不同农户在磷肥的施用上存在较大差异;其次为全氮和有机质，变异系数分别为 24.59%和 24.79%，为中等变异(表2).

表2 土壤养分的空间变异Table 2 Spatial variations of soil nutrients

2.3 土壤养分(基本肥力)与产量之间的数学模型

采用三次曲线模型拟合土壤养分与产量之间的关系，得到数学模型为:

对模型进行方差分析(表3)，可知该模型达到极显著水平(F=3.78)，相关系数 R=0.78，决定系数R2=0.608 4，说明产量的总变异中有60.84%可以由土壤养分的协变关系来解释.表明模型与实际情况拟和较好，可用此模型对小麦产量进行初步分析和预测.

表3 土壤养分与产量数学模型的方差分析Table 3 Analysis of variance of mathematical model among soil nutrients and yield

考虑到鹤壁市小麦旱地土壤有机质含量中等(均值 为14.6)，且短期内年际间差异不大，空间变幅也较小(变异系数为24.79%)，故为简便起见，在模型分析中将其看作固定因素.于是，模型简化为二元三次曲线模型:

2.4 土壤全氮含量与产量之间的关系

图2表明，在土壤速效磷含量保持样点平均水平(15.31 mg·kg-1)不变时，土壤全氮含量与旱地小麦产量之间的关系比较复杂.土壤全氮含量在0.75 ～1.2 g·kg-1时，随着全氮含量的增加，产量有明显递增趋势;土壤全氮含量为1.2 g·kg-1时，产量达到最高;但当土壤全氮含量为1.21～1.9 g·kg-1时，随着土壤全氮含量的增加，产量呈明显递减趋势，其后，则又呈递增趋势.这就说明，在土壤速效磷含量维持在样点平均水平状态时，土壤全氮含量与小麦产量之间的关系并不完全具有正相关关系，而是具有明显的阶段性.

图2 土壤全氮含量与产量之间的关系Fig.2 Relationship between the soil total nitrogen content and the wheat yield

2.5 土壤速效磷含量与产量之间的关系

由图3看出，在土壤全氮含量保持样点平均水平(1.25 g·kg-1)不变时，土壤速效磷含量与旱地小麦产量之间的关系呈现2个阶段的变化:第1个阶段，在土壤速效磷含量为5～32 mg·kg-1时，小麦产量随着土壤速效磷含量的增加而提高，当土壤速效磷含量达到32 mg·kg-1时，小麦产量达到最高;第2个阶段，当土壤速效磷含量大于32 mg·kg-1时，小麦产量则呈现逐步下降的趋势.

图3 土壤速效磷含量与产量之间的关系Fig.3 Relationship between the soil available phosphorus content and the wheat yield

2.6 土壤全氮含量、土壤速效磷含量与产量的效应曲面图

据模型(2)，依其理论估算值(略)可绘制出土壤养分效应曲面图(图4).

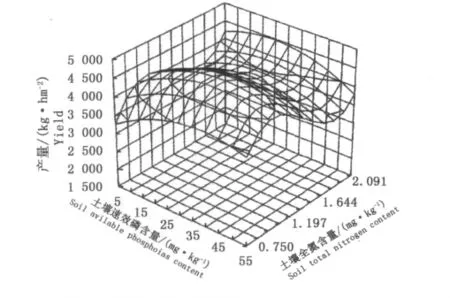
图4 土壤全氮、速效磷含量与产量的效应曲面图Fig.4 A response surface figure among soil total nitrogen content，available phosphorus content and yield

由图4可以看出，当分别固定不同土壤全氮含量不变时，随着土壤速效磷含量的增加，小麦产量呈现类似图2的“低—高—低—高”的阶段性变化趋势;当固定不同土壤速效磷含量不变时，随着土壤全氮含量的增加，小麦产量则呈现类似图3的“低—高—低”的阶段性变化趋势.所不同的是图2、图3反映了将土壤全氮含量、土壤速效磷含量分别固定在样点平均值时的产量变化趋势，而图4则更全面地反映了不同土壤全氮含量或不同土壤速效磷含量分别固定在不同水平时的产量变化趋势.从该效应曲面图中，我们可以直观地看出不同产量水平范围内适宜的土壤养分含量区域，对于合理施肥具有一定指导意义.

2.7 最高产量与最佳经济土壤养分含量

2.7.1 最高产量土壤养分含量 根据模型(2)，分别对土壤全氮(N)、速效磷(P)求偏导，得到最高产量偏微分联立方程组:

求方程组的解，得到2组解:N=1.87 g·kg-1，P=27.88 g·kg-1和 N=1.22 g·kg-1，P=34.33 g·kg-1.代入模型(2)，比较产量结果预测值，可知与最高产量(4 743.36 kg·hm-2)相适应的土壤全氮含量为1.22 g·kg-1，土壤速效磷含量为34.33 mg·kg-1，即为土壤养分效应曲面中的最高点所对应的土壤全氮含量与土壤速效磷含量(图4).

由此可见，在土壤有机质稳定在14.6 g·kg-1的前提下，鹤壁市旱地小麦要获得高产，土壤中全氮含量(1.25 g·kg-1)完全可以满足小麦生长需要，而土壤速效磷含量(15.31 mg·kg-1)却需要通过施肥补充35.06-15.31=19.75 mg·kg-1，按每公顷土壤耕层土2.25×106kg计算，每公顷施入15 kg P2O5可提高土壤速效磷含量6.67 mg·kg-1，则需要向土壤中补充速效磷19.75×15/6.67=44.42 kg·hm-2，考虑到土壤对磷的固定作用和肥料利用率，即需施入优质过磷酸钙(有效磷含量18%)44.42/(0.2 ×0.18)=1 233.89 kg·hm-2.2.7.2 最佳经济土壤养分含量 按照目前市场价格，小麦2.06 元·kg-1，纯氮 7.56 元·kg-1，纯磷7.573元·kg-1，则据模型(2)，分别对土壤全氮(N)、速效磷(P)求偏导，得到最佳经济土壤养分偏微分联立方程组:

解此方程组，可得到2组解:N=1.2 g·kg-1，P=31.86 mg·kg-1和 N=1.87 g·kg-1，P=25.32 mg·kg-1.代入模型(2)，比较产量预测值，可知第1组解产量最高(4 750.69 kg·hm-2).即在土壤有机质保持样点平均值14.6 g·kg-1不变时，最佳经济土壤全氮含量为1.2 g·kg-1，土壤速效磷含量为31.86 mg·kg-1为宜.换言之，鹤壁市旱地小麦土壤全氮含量为1.2 mg·kg-1和土壤速效磷含量为31.86 mg·kg-1时可以满足经济最佳产量4 750.69 kg·hm-2的需求.

2.7.3 土壤养分与产量数学模型在生产实践中的应用 建构与解析土壤养分与产量数学模型的目的在于建立施肥决策系统，指导农户合理施肥，提高小麦产量.如前所述，土壤有机质含量年际间变异较小，所以为简便起见，在指导农民合理施肥时，将土壤有机质含量测定值直接代入模型(1)进行运算即可.以样点1(农户1)土壤养分测定值为例说明指导农民合理施肥的具体过程.

由表1知，样点1(农户1)土壤有机质含量为10.6 g·kg-1，全氮含量为 1.9 g·kg-1，速效磷含量为11.6 mg·kg-1，小麦实测产量为 4 200 kg·hm-2.将土壤有机质含量代入模型(1)并分别求导，得到偏微分联立方程组.解此方程组，可得到2组解:N=1.12 g·kg-1，P=36 g·kg-1和 N=1.01 g·kg-1，P=28.5 g·kg-1.

经代入模型比较产量结果预测值发现，第1组解的产量最大(5 244 kg·hm-2).因此，认为样点1(农户1)要获得最高产量，土壤全氮含量和速效磷含量以 N=1.12 g·kg-1，P=36.2 mg·kg-1为宜.而该农户土壤全氮实际含量测定值为1.90 g·kg-1＞1.12 g·kg-1，因此能够满足小麦生长需要;速效磷含量实际测定值为11.6 mg·kg-1，极度缺磷，故需要补充 36.2-11.6=24.6 mg·kg-1.即需要向土壤中补充24.6 ×15/6.67=55.32 kg·hm-2，也就是说，应当施入优质过磷酸钙肥料(有效磷含量18%)55.32/(0.2 ×0.18)=1 536.67 kg·hm-2.

3 结论与讨论

土壤养分是小麦产量形成的重要物质基础之一.因此，研究土壤养分与小麦产量之间的关系至关重要.然而，迄今为止，大多研究都是从施肥的角度出发，来探讨施肥量与小麦产量之间的关系并建立数学模型，而土壤养分与产量之间关系的研究虽然也有少量报道［8～11］，但很少涉及数学模型的构建.本研究以土壤养分为自变量因素，建立了小麦产量与土壤全氮、速效磷、有机质之间的数学模型，弥补了上述研究的不足，从而为测土施肥提供了一条新的思路和途径.

建立土壤养分与产量数学模型的优点在于指导农民施肥具有明显的针对性，即可以根据各农户土壤养分测定数据，“对症下药”，做到“一个地块，一个施肥指导方案”.而通常建立的施肥模型则针对性不强，只能给出某土壤类型或某生态类型区一定产量水平下的施肥方案，不能具体到某农户或某地块.事实上，小麦产量的形成是土壤养分与施肥养分共同作用的结果.因此，无论施肥量与产量模型，还是土壤养分与产量模型都带有一定程度的局限性.

［1］ 陈新平，张福锁.通过“3414”试验建立测土配方施肥技术指标体系［J］.中国农技推广，2006(4):36-39.

［2］ 高祥照，马常宝，杜 森.测土配方施肥技术［M］.北京:中国农业出版社，2005.

［3］ 王圣瑞，陈新平，高祥照，等.“3414”肥料试验模型拟合的探讨［J］.植物营养与肥料学报，2002，8(4):409-413.

［4］ 王兴仁，张福锁.现代肥料试验设计［M］.北京:中国农业出版杜，1996.

［5］ 时 燕.崇明岛轻质土壤小麦配方施肥研究［J］.上海农业学报，2010，26(3):134-137.

［6］ 李若楠，张彦才，王丽英，等.晚播小麦优质高产施肥数学模型研究［J］.河北农业大学学报，2007，30(4):1-4.

［7］ 陈伦寿，李仁岗.农田施肥原理与实践［M］.北京:农业出版社，1984.

［8］ 薛正平，杨星卫，段项锁，等.土壤养分与春小麦产量关系及最佳施肥量研究［J］.中国生态农业学报，2004，12(4):110-112.

［9］ 姜 勇，张玉革，梁文举，等.沈阳市苏家屯区耕层土壤养分空间变异性研究［J］.应用生态学报，2003，14(10):1673-1676.

［10］ 张建杰，李富忠，胡克林，等.太原市农业土壤全氮和有机质的空间分布特征及其影响因素［J］.生态学报，2009，29(6):3163-3172.

［11］ 赵克静，刘厚军，李德明.土壤有机质含量对春小麦产量贡献率的研究［J］.现代化农业，2001(5):23-24.