基于多连杆的机器人步行机构运动特性分析*
2012-04-12李鹏辉
李鹏辉
(湖北科技职业学院 武汉 430074)
随着机器人应用领域不断扩大,人类对机器人的研究也更加深入.一种新型的移动机构成为了研究移动机器人[1]的热点——轮腿式移动机构[2].这种移动机构使移动机器人具有速度快、稳定性好以及对地面的适应能力强的特点.在研究设计机器人步行系统过程中,通过比较若干机构的优缺点后,最终选择了步行式六足机构[3-4]的方案.步行式结构的优点是每个支腿仅需要一个电机驱动,但是要保证机构运动的整体平稳性,就必须对落足点的运动轨迹提出较高要求,即一个周期的运动轨迹要较好地满足:前半个周期实现迈步动作,落足点尽可能的高于地面,并有一定的水平位移;后半个周期使落足点回到初始位置,并保证其轨迹尽可能的与地面平行.步行机构设计为多连杆机构,单个四连杆机构的运动分析已有文献[5-8]论述,本文从理论上分析所设计步行机构运动的可行性,并予以仿真验证.
1 步行机构的简化
步行机构为多连杆机构,共6组,每组结构相同,前后各3个轮腿,见图1.该机构采用1台电机,通过机构传动,来实现落足点周期性的运动,从而实现机器人的前进、后退以及一定范围内的越障.机构简图见图2.
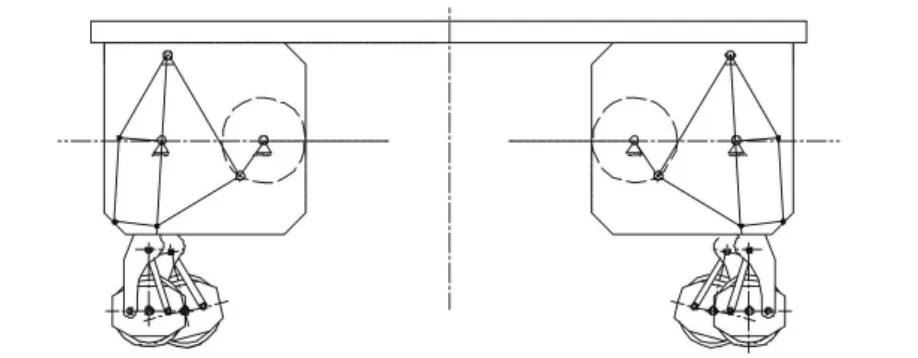
图1 步行机构示意图
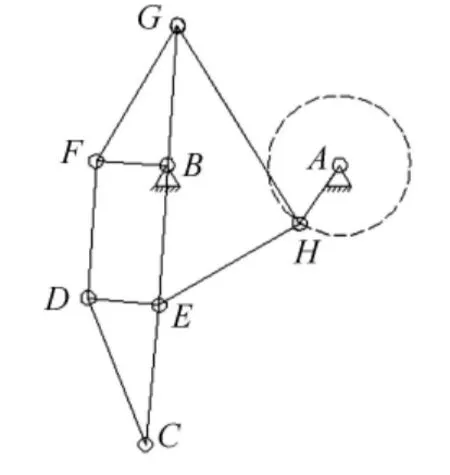
图2 轮腿机构简图
由图2可看出,整个轮腿机构可以分为相互协调的3个四连杆机构和2个三角架,四连杆机构和三脚架之间以及四连杆机构之间都通过共用连杆来传递运动.为实现整个机构协调运动,所有连杆均为铰接连接.
2 步行机构的运动学分析
由图2可看出,杆AH,GH,BG,车架构成一个四连杆机构,杆AH,BE,EH,车架构成一个四连杆机构,杆DE,DF,BE,BF构成一个四连杆机构.而杆CD,CE,DE和杆BF,FG,BG分别构成2个三脚架.A,B两点均固定在车架上,C点为落足点(机器人车轮中心).曲柄AH同时充当其中2个四连杆机构的曲轴,作圆周运动.这样,在曲轴的圆周运动过程中,落足点C也将随连杆机构做周期性的运动,从而实现一个周期的行走运动.
2.1 上四连杆机构的运动学分析
机构实际工作时,摆杆始终位于固定点B的上方,称为上四连杆机构,见图3.点O为坐标系的中心.
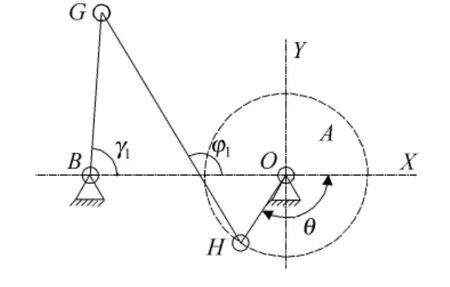
图3 上四连杆机构
设曲柄AH长度为l1,且与水平轴X的夹角为θ,连杆GH长度为l2与X轴的夹角为φl,摆杆BG长度为l3与X轴为γl.固定点A,B间的距离为l.曲柄AH绕固定点A作圆周运动,摆杆BG绕固定点B从动.可得如下平衡方程组:
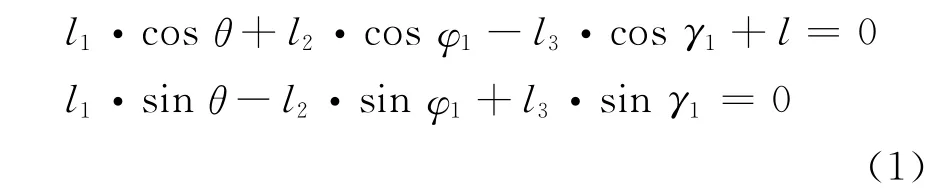
由式(1)可解得在任意时刻摆杆BG、连杆GH与X轴的夹角γ1和φ1.
2.2 下四连杆机构的运动学分析
机构实际工作时,摆杆始终位于固定点B的下方,称为下四连杆机构,见图4.点O为坐标系的中心.
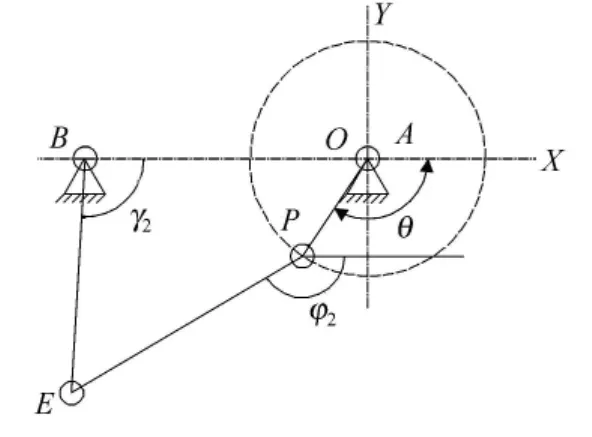
图4 下四连杆机构
设曲柄AH长度为l1,且与水平轴X的夹角为θ,连杆EH 长度为l4与X轴的夹角为φ2,摆杆BE长度为l5与X轴为γ2.固定点A、B间的距离为l.曲柄AH绕固定点A作圆周运动,摆杆BE绕固定点B从动.可得如下平衡方程组:
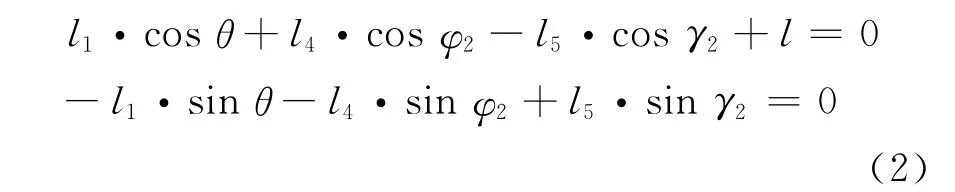
由式(2)可解得在任意时刻摆杆BE、连杆EH与X轴的夹角γ2和φ2.
2.3 落足点C的运动学分析
图2中,连杆DE,DF,BE,BF构成一个平行四边形机构,连杆DE和BF 始终平行,连杆DE,BF长度相同,连杆CE,BE,BG,DF长度相同.在以图3、图4所示O点为中心的坐标系中可得出落足点C的坐标为
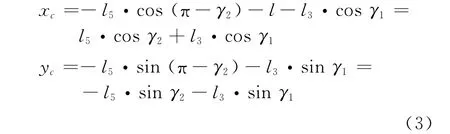
由式(1)~(3)可以看出,在任意时刻,曲柄AH的运动状态决定落足点C的位置.
3 仿真结果及分析
连杆机构各杆件所设计的长度分别取l=240mm,l1=100mm,l2=l4=330mm,l3=l5=200mm.假设曲柄AH 以某一转速绕A点作匀速转动,利用MATLAB软件对落足点C进行一个周期的仿真,可得到轨迹曲线见图5.
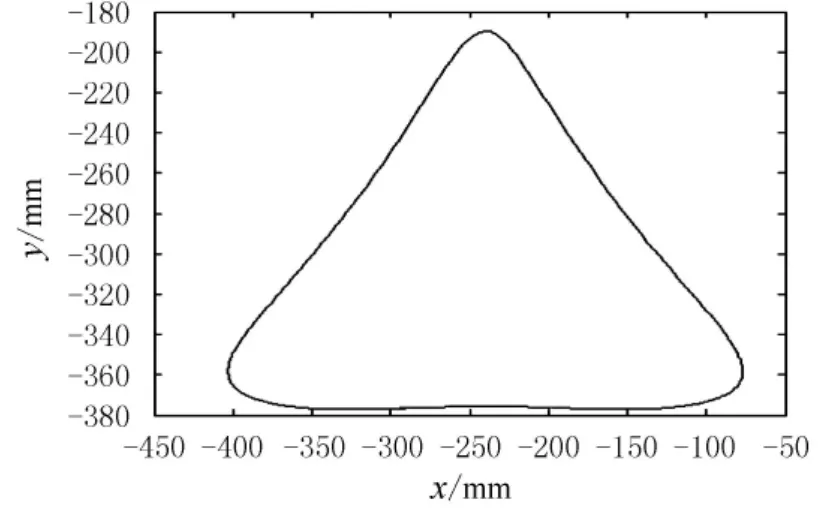
图5 落足点C的运动轨迹曲线
由图5可看出,整个运动轨迹呈三角形,水平位移的最大值位于半个周期的时间上,即迈步周期的末端和平移周期的始端,垂直位移的最大值出现在3/4周期,即迈步周期的中点.该运动轨迹函数在平移周期基本保持与水平轴的平行,在迈步周期前1/2周期呈单调递增,后1/2周期呈单调递减.
通过对步行机构落足点C的运动仿真结果可以看出,落足点C在迈步周期的最大垂直抬升高度为187mm,最大水平位移为326mm.从水平位移和垂直位移上来讲,迈步周期C点的运动轨迹都能很好地达到机器人行走所需要的位移量,而且在平移周期,曲线较平坦,其平坦部分最大垂直偏移量仅相差1.3mm,基本保证了整个机构与水平地面等距离平行移动.
为了研究各杆件长度对步行机构运动特性的影响,对所设计的l,l1,l2(l4),l3(l5)4组参数,分别保持其中3组参数不变,调整另一组参数,对步行机构落足点C进行运动仿真.仿真得到的运动轨迹图形状相似,但落足点C的最大垂直抬升高度及最大水平位移均发生变化,见表1~表4.

表1 不同l下的变化 mm
由表1可见,l增大,C点最大抬升高度减小,最大水平位移减小.反之,则最大抬升高度增大,最大水平位移增大.

表2 不同l1下的变化 mm
由表2可见,l1增大,C点最大抬升高度增大,最大水平位移增大.反之,则最大抬升高度减小,最大水平位移减小.

表3 不同l2,l4下的变化 mm
由表3可见,l2,l4增大,C点最大抬升高度增大,最大水平位移减小.反之,则最大抬升高度减小,最大水平位移增大.

表4 不同l3,l5下的变化 mm
由表4可见,l3,l5增大,C点最大抬升高度减小,最大水平位移增大.反之,则最大抬升高度增大,最大水平位移减小.
4 结 论
通过运动分析和仿真,所设计机器人步行机构运动轨迹满足步行机构的一般要求,并且该机构驱动形式简单,对控制系统要求不高.针对该行走机构的特点,在保证满足曲柄摇杆机构条件的基础上,还可以对各个杆件的长度作进一步的调整、优化及组合,以得到更为理想的运动轨迹曲线或达到克服一定障碍的目的.
[1]徐国华,谭 民.移动机器人的发展现状及其趋势[J].机器人技术与应用,2001(3):7-14.
[2]王劲松,樊鑫国,王 洋,等.基于曲柄摇杆机构的新型六足爬行机器人的设计[J].中国工程机械学报,2008,6(4):448-453.
[3]OENNAU A,KERSCHER T,DILLMANN R.Design and kinematics of a biologically-inspired leg for a six-legged walking machine[C]//Biomedical Robotics and Biomechatronics(BioRob),2010 3rd IEEE RAS and EMBS International Conference on 26-29Sept.,2010:626-631.
[4]STOICA A,CARBONE G,CECCARELLI M,et al.Cassino hexapod:experiences and new leg design[C]//Automation Quality and Testing Robotics(AQTR),2010IEEE International Conference on 28-30May 2010:338-343.
[5]雷 培,刘云霞.基于 MATLAB的四连杆机构运动分析[J].机械工程与自动化,2009,153(2):74-78.
[6]毛 新,罗庆生,韩宝玲.仿生六足爬行机器人运动控制技术研究[J].计算机测量与控制,2006(3):55-58.
[7]张之璐,彭光正,朱智乾.气动人工肌肉驱动器驱动六足爬行机器人的步态选择和结构设计[J].液压与气动,2004(4):42-46.
[8]韩建海,赵书尚,李济顺.六足机器人行走步态的协调控制[J].机电工程,2004(4):70-73.
