基于粗糙集-神经网络的飞机寿命消耗量预测模型研究

安 航，王 瑛，冯博宇

AN Hang,WANG Ying,FENG Bo-yu

（空军工程大学 工程学院，西安 710038）

0 引言

随着现代科学技术的快速发展，以及军事斗争准备工作的不断深入，飞机的使用强度越来越大。我国规定同型飞机的平均剩余寿命百分比不能低于一定的比例，为航空工程保障计划的顺利实施，需经常安排好飞机的使用和保持最大数量的飞机处于良好状态，这就对飞机的使用寿命提出了更高的要求。飞机寿命资源的消耗量直接影响到寿命资源的存储量（即可用飞行小时），飞机寿命资源存储量是开展各种飞行活动和任务的根本基础。因此，构建模型实现对飞机寿命资源消耗量的准确预测，可以进一步完善飞机寿命管理方法，使得飞机做到物尽其用[1]。

目前针对飞机寿命的研究较多，文献[2]研究了飞行强度对使用寿命的影响；文献[3]研究分析了腐蚀环境对飞机结构和使用寿命的影响；何宇廷提出了飞机结构寿命包线的建立方法[4]。然而文献中分析并预测在使用过程中飞机寿命资源消耗的论述较少，基于此，笔者融合粗糙集方法和人工神经网络技术各自的优势，在不改变样本分类质量的条件下，运用粗糙集理论约简样本指标，确定网络输入层变量和神经元个数[5]，建立基于粗糙集-神经网络的飞机寿命资源消耗量预测模型，并应用这一非线性模型对飞机寿命资源消耗量进行了预测。

1 基于RS-BP神经网络的飞机寿命消耗量预测模型的建立

结合粗糙集属性约简的特点和神经网络对复杂函数全局逼近的优势[6]，本文采用基于RS-BP神经网络的智能建模方法对飞机寿命资源消耗量进行预测。因为航空装备的使用以及管理一般是成建制进行的，所以，在研究飞机寿命消耗量时，以机群为研究对象更有意义。首先全面考察影响飞机寿命资源消耗量的因素，然后使用粗糙集理论针对决策属性来约简条件属性，从条件属性中去掉对于决策属性而言冗余的（或相对不重要的）属性，随后我们将这些约简后的条件属性（影响因素）和决策属性（消耗量）作为神经网络的输入和输出数据进行训练，最终得到影响因素和飞机寿命消耗量之间的映射关系。构建基于RS-BP神经网络模型的步骤如图1所示。

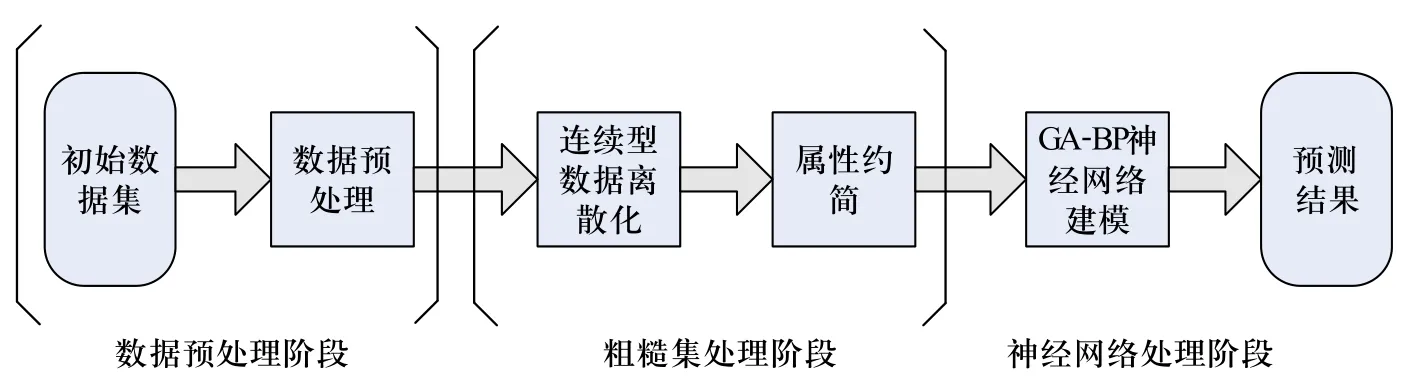
图1 基于RS-BP神经网络建模流程

1.1 原始数据预处理

由于现实中所采集数据的度量单位不同，各维数据值相差也较大，如果不对这些数据进行处理或选择，而直接用粗糙集算法进行属性约简，势必会造成效率较低，所以在使用约简算法前，应先将原始数据进行规范化处理。

最小-最大规范化方法：

假定min和max分别为变量的最小值和最大值，通过

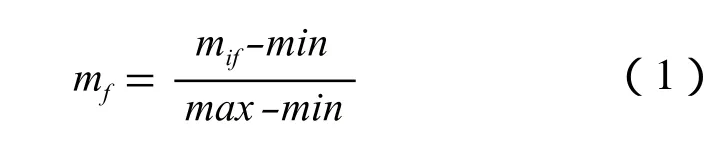
可将的区间映射到[0,1]区间。这里的x1f,x2f,…,x1f是的f几个度量值。

1.2 连续属性离散化

由于粗糙集理论无法直接使用连续型数据，所以在使用粗糙集理论进行属性约简前需先对具有连续值特征的属性进行离散化。经过离散化之后，原来的决策系统被一个新的决策系统所代替，且不同的断点集会将决策系统转换成不同的决策系统。由于最终的决策属性值均为一维的，故对决策列采用较为简单且成熟的K-means值聚类法进行离散化[7]。

粗糙集理论中对连续属性离散化的方法很多，在这里采用苗夺谦[8]提出的基于动态层次聚类的连续属性离散化算法。其的指导思想是在保证离散后的决策表应当同离散化前一样保持其相容性的前提下，寻找使得约简效率最高的聚类划分。该算法无需事先指定聚类的数目，而是根据聚类后的决策表相容度的限制条件、聚类的距离阀值实现自动聚类。

1.3 对离散化后的样本数据属性约简

通过属性约简可以去除冗余的或对寿命消耗量预测结果影响不大的属性，以减少属性数目，提高分析效率。文献[9]提出的基于系统正域的属性主要性的数据约简方法，尽管不能保证一定能够找到系统信息的最优解，但笔者认为依据单个属性重要的约简算法依然具有合理性。其算法得到的约简即使不是最优约简，健壮性和稳定性也是较好的。因此本文采用基于属性重要性的约简方法作为粗糙集的数据约简算法。具体步骤如下：

1）REDU=核；

2）候选属性集AR=C－REDU；

3）找出AR中具有最大属性重要性SGF (a,R,D)的属性a；

4）如果有多个属性ai(i=1,,m)具有相同的最大重要性，则选取与REDU具有最小属性取值组合的属性ai；

5）REDU=REDU ☒ {aj}；AR=AR － {aj}；

6）如果K(REDU,D)=1，则算法中止，否则转回3)。

1.4 利用属性约简结果建立基于遗传算法优化的BP神经网络模型

应用遗传算法优化BP神经网络[10]的详细步骤如图2所示。

图2 GA-BP算法详细步骤

由上一节属性约简所确定的属性数量作为网络输入向量，接下来则要考虑网络的结构设计，由于影响网络泛化能力的因素与研究问题的复杂程度、网络结构的选择等诸多因素有关，因此BP网络结构的确定要根据实际问题来决定。

1.4.1 网络结构的确定

一个S型隐含层加上一个线性输出层的BP网络，能够逼近任何在闭区间内的一个连续有理函数[11]，因而一个三层的神经网络就具有模拟任意复杂的非线性映射的能力，并且可以通过增加隐含层神经元的个数来提高网络的精度。

隐含层神经元个数的确定目前还没有统一的方法，本文采用试算法来确定隐含层的神经元个数：开始根据经验公式使用很少的隐含层神经元数对网络进行训练和测试，然后不断增加隐含层神经元数，比较不同训练和测试的结果，最终选取合适的隐含层神经元个数。

1.4.2 采用GA算法优化权值和阀值

BP神经网络采取的权值更新方法为最速梯度下降法，其缺陷是容易陷入局部极小、收敛速度慢[12]。本文采用遗传算法来优化初始权值、阀值，主要步骤如下：

1）种群初始化，包括交叉概率Pc、交叉规模、突变概率Pm以及初始化w1ij、w1jk、q1j和q1k进行；采用实数编码，初始种群取50各个体均是由w1ij、w1jk、q1j和q1k四部分组成的实数串；

2）各个体评价函数计算，进行各个体排序。按照下式概率值进行网络个体的选择。

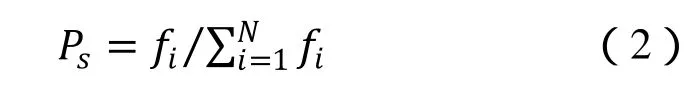
其中为个体的适配值，可用误差平方和E来衡量，即：

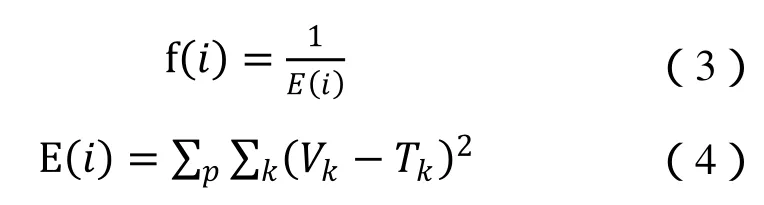
其中，i=1,2,…,N为染色体数；k=1,…,4为输出层节点数，本文中k取1；p=1,…,10为训练样本数；Tk为预期输出值。

3）按照概率Pc对个体Gi和Gi+1交叉操作，从而产生新个体和，未进行交叉操作的个体，则直接进行复制。

4）运用概率Pm突变，从而产生Gj的新个体；

5）将新个体插到种群P中，并且计算其评价函数；

6）计算误差平方和，如果达到预定值εGA，那么转(7)。反之，则转入(3)，继续执行遗传操作；

7）将GA输出的优化初值作为阈值和初始权值。再用BP算法训练网络，直到达到指定精度εBP(εBP<εGA)。

1.4.3 预测结果评价参数

选择平均相对误差MAPE、相关系数R、输出数据可行度Z三个参数来评价神经网络预测结果的预测精度。因为它们既不受样本规模的影响，又不受样本单位的制约，便于将预测结果与前面的线性预测方法进行对比，其公式表示为：

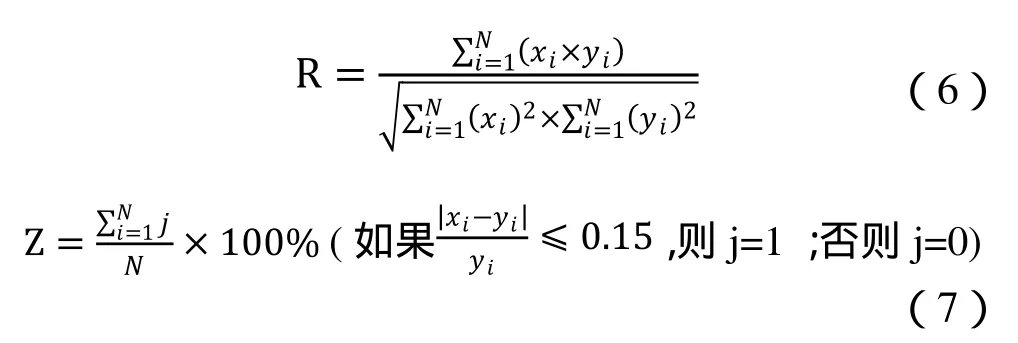
其中xi代表模型模拟输出值，yi表示实测值。平均相对误差MAPE反映了预测值的总体质量，相关系数R反映了观测值的变化对预测值的影响，输出数据可信度Z反映了预测值在给定的可信度内的分类精度。

2 飞机寿命消耗量预测实例

运用具体数据和已建立的模型，预测飞机寿命资源的消耗量。选取某单位2007-2009每月飞行数据，对原始数据进行变换处理后如表1所示。

结合实地调研结论，将影响飞机寿命资源消耗量的因素归纳为以下5种，即：当月飞行训练消耗量M、恶劣天气占当月的比例U、调出飞机消耗量N、事故P、机务素质差的机务人员所占的比例Q。

2.1 连续属性离散化

将表1中原始数据预处理后，使用K-means法和文献[8]中的算法对决策属性和条件属性进行离散化。将决策属性（飞机寿命资源消耗量）和条件属性（当月飞行训练消耗量、恶劣天气占当月的比例、调出飞机消耗量、事故、机务素质差的机务人员所占的比例）进行分类从而将连续属性离散化，离散结果如下：

每月飞机寿命总消耗量：{1：[0，0.059]；2：[0.078，0.139]；3：[0.167，0.227]；4：[0.307，0.394]；5：[1，1]}。

当月飞行训练消耗量：{1：[0，0.195]；2：[0.3，0.356]；3：[0.388，0.455]；4：[0.598，0.758]；5：[0.825，1]}。

恶劣天气占当月的比例：{1：[0，0.221]；2：[0.279，0.485]；3：[0.618，0.765]；4：[0.824，1]}。

调出飞机的寿命消耗量：{1：[0，0]；2：[0.531，0.766]；3：[0.813，1]}。

机务素质差的机务人员所占的比例：{1：[0，0.077]；2：[0.154，0.269]；3：[0.462，0.731]；4：[0.769，1]}。

对于飞行事故，可将其属性值量化为1、2。其中1表示没有发生飞行事故，2表示发生飞行事故。

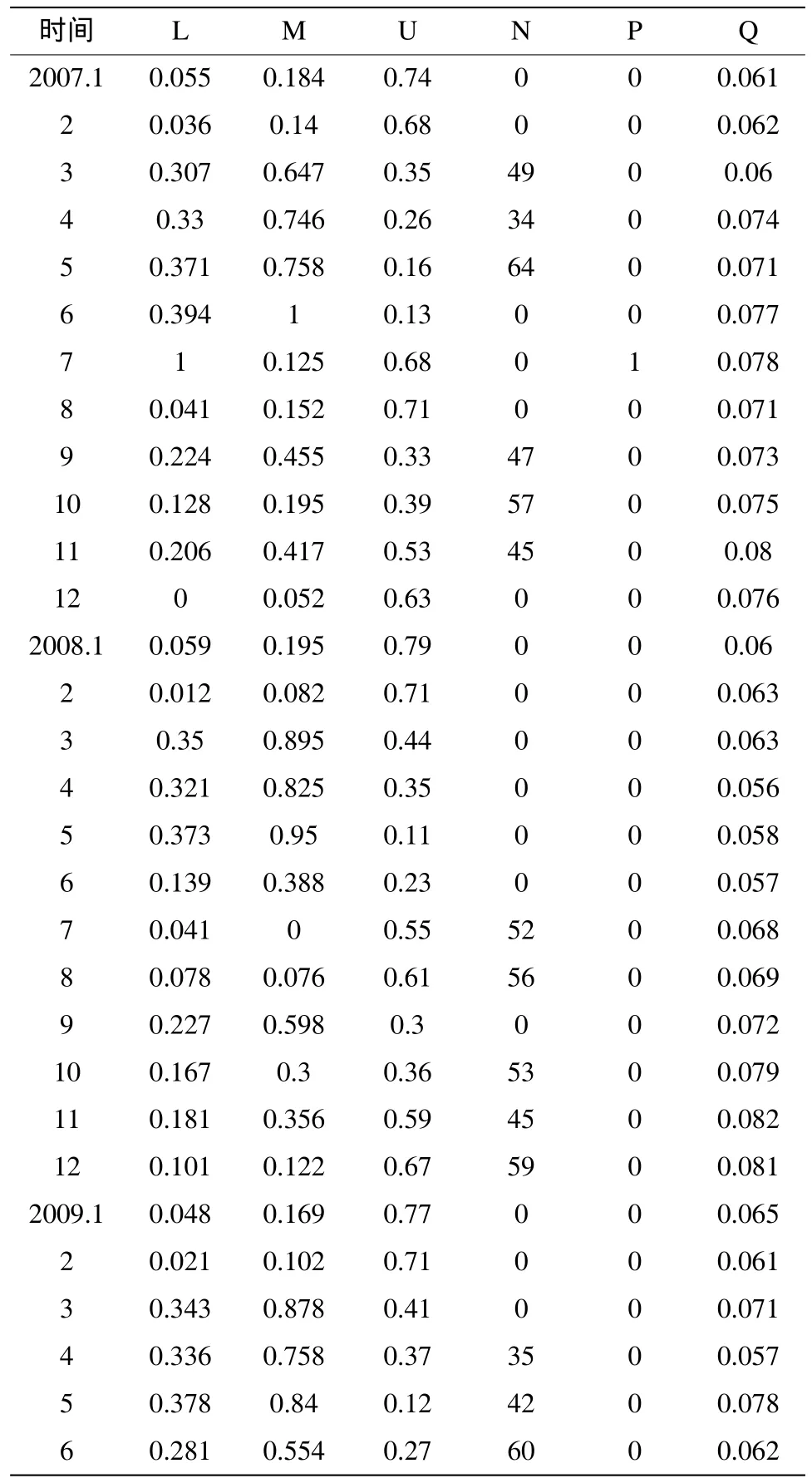
表1 某单位飞机寿命消耗统计数据

2.2 属性约简

属性约简的步骤为，首先求出属性规约集的核心，然后运用约简算法计算归约集，并根据某种评判标准确定最佳归约集。

令D=决策属性集={D}={L}，C=条件属性全集={C}={M，U，N，P，Q}

首先计算得到Card(POSC(D))=24，计算系统的核为：{当月飞行训练消耗量，恶劣天气占当月的比例}，由REDU={当月飞行训练消耗量，恶劣天气占当月的比例}，Card(POSCred(D))=14，而后计算其余属性的重要性为：

SGF(N,REDU,D)=12/24，SGF(P,REDU,D)=3/24，SGF(POSCred(D))=3/24

属性N的重要性最大，因此将该属性加入到中，由于此时,因此算法中止。最终得到的属性约简结果为：{当月飞行训练消耗量，恶劣天气占当月的比例，调出飞机消耗量}。

2.3 仿真验证与分析

由上节粗糙集属性约简结果分析可知，网络的输入层节点数为3，输出层节点数为1，下面需要确定隐层节点的个数。本文采用试凑法，先通过经验公式给出隐层节点数，而后逐渐增加或减少隐层单元数，最后依据网络均方误差最小的原则（或较快的收敛速度）确定网络的隐层节点数。经过验证，当隐含层单元数为8时，训练误差和学习步数都比较理想，因此网络结构为3-8-1，3个输入层节点分别对应当月飞行训练消耗量、恶劣天气占当月的比例、调出飞机消耗量，8个隐层神经元，1个输出层节点对应飞机寿命资源消耗量。

采用Matlab神经网络工具箱，取表1中前24组为训练样本，后6组为检验样本。在样本训练过程中，种群规模50，遗传代数110，交叉概率为0.7，变异率为0.01训练步数为1000，误差为1.00E-13，当训练步数为144时，期望输出值与实际输出值的训练误差达到设定要求，BP-GA网络训练误差变化如图3所示。

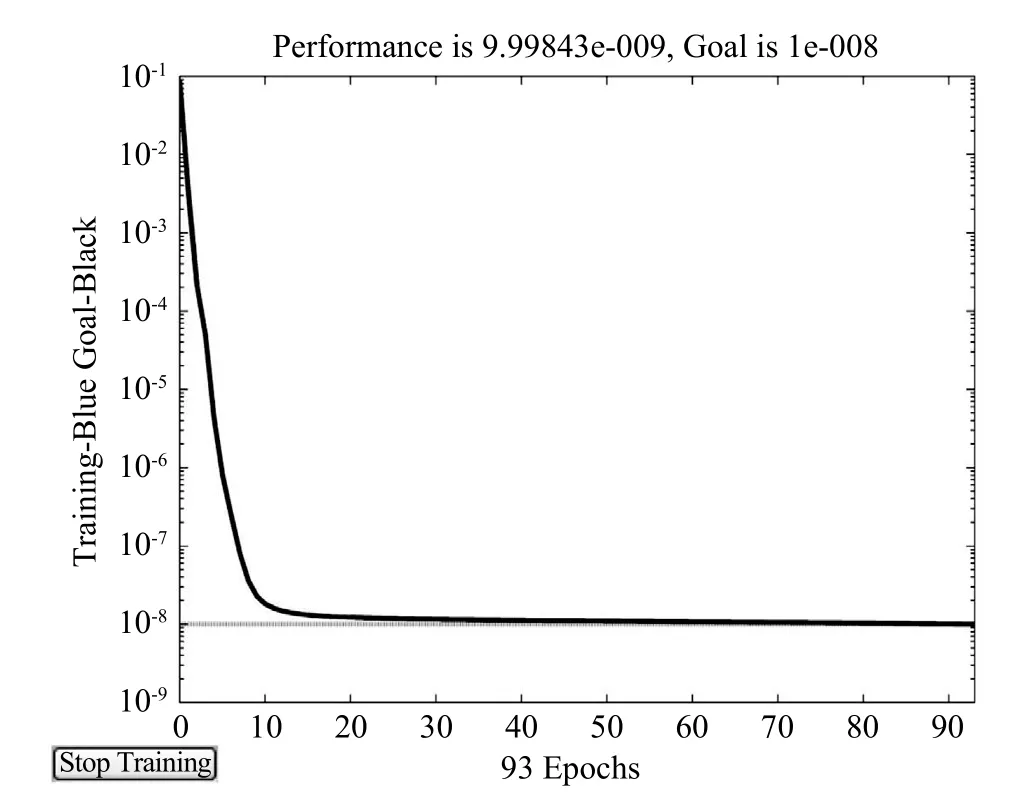
图3 训练误差变化

为了检验网络的泛化能力，取2009年1-6月的寿命消耗量数据对网络进行检验。将数据归一化处理后，用训练好的网络进行预测，预测结果如表2所示。除6月份的预测结果外，其余相对误差均在较低的水平。

为了验证经过粗糙集属性约简后的影响因素具有较高的可信度，取未经过粗糙集约简的全指标体系（当月飞行训练消耗量、恶劣天气占当月的比例、调出飞机消耗量、事故、机务素质差的机务人员所占的比例）作为输入元素，输出为飞机寿命资源消耗量，其他条件不变，网络训练误差变化如图4，预测结果如表3所示。

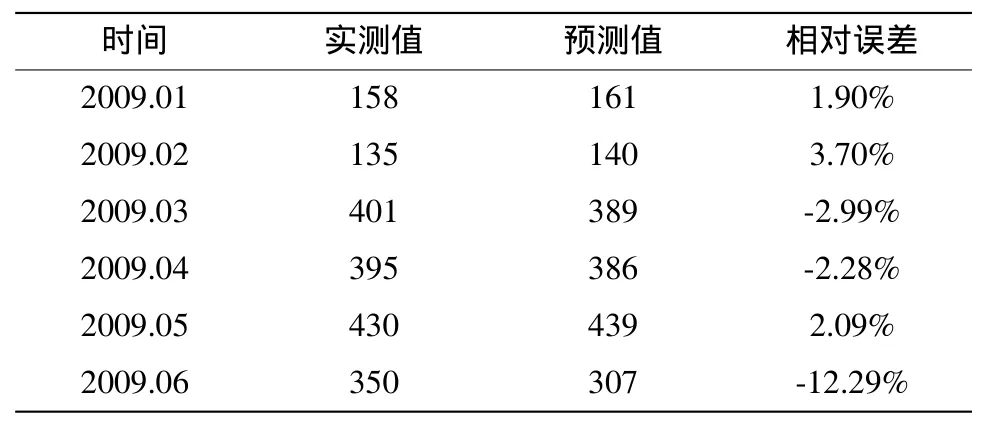
表2 神经网络预测结果

图4 训练误差变化

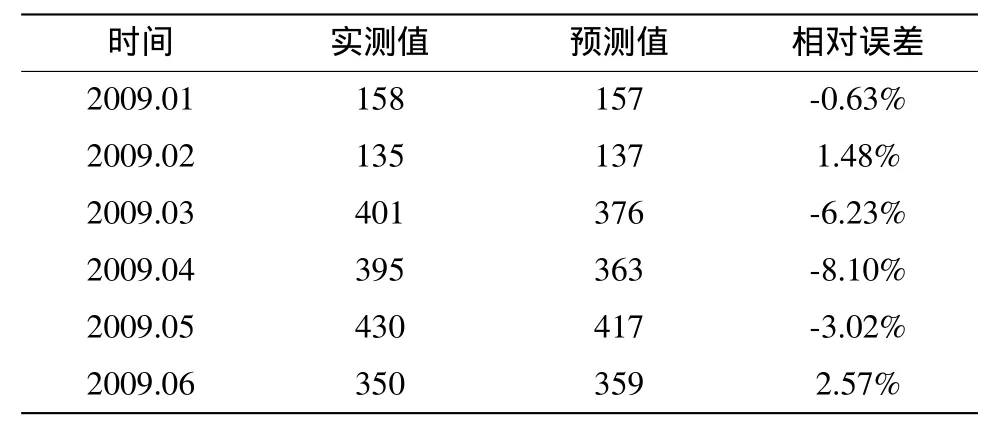
表3 神经网络预测结果

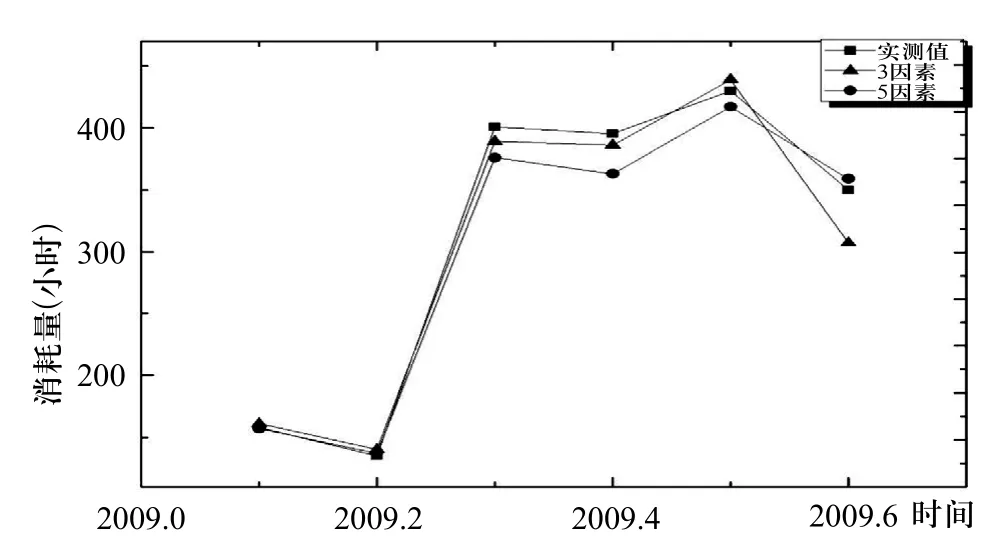
图5 神经网络预测结果与实际结果对比

由图5可以看出，两种预测模型的预测结果与实测值的拟合度高，无论对于平稳数列还是在有数据波动的情况下，都表现出良好的预测能力。

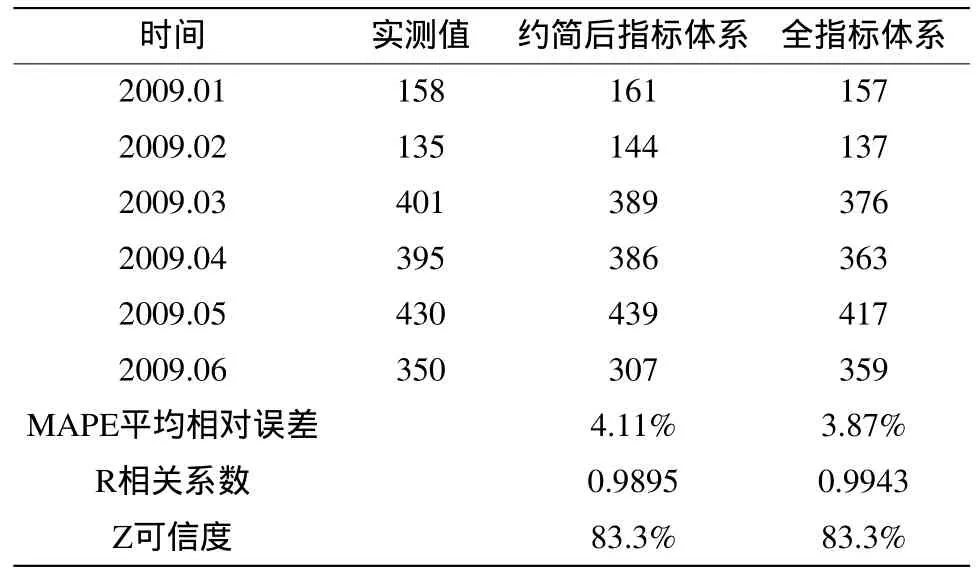
表4 预测结果比较

表4给出了经过粗糙集属性约简的BP神经网络寿命消耗量预测模型，与没有进行属性约简的BP神经网络预测模型的预测结果比较。两种预测方法的可信度都为83.3%，经过属性约简的神经网络模型的MAPE仅为4.11%，虽比未进行属性约简的BP预测模型的MAPE略高，但两个模型的平均相对误差均处于较低的水平，保证了模型预测的准确性。

3 结论

1）利用粗糙集理论来化简样本及条件属性，通过属性约简求核，筛选分析出了对飞机寿命资源消耗量影响较大的因素，从而简化了网络输入变量的个数，减少了网络的训练时间，改善了学习的效率。

2）应用实测数据进行仿真，结果表明，属性约简后的指标体系与原有全指标体系对于寿命消耗量的预测有同样的效果，与实际值拟合度高，平均相对误差小，通过粗糙集属性约简去除了对飞机寿命消耗影响不大的、冗余的因素，证明了粗糙集是神经网络样本分析及处理的有效方法。

3）将粗糙集理论与GA-BP神经网络算法结合，应用于飞机寿命消耗量预测的方法使得预测结果准确、可靠，具有较高的实用价值。此研究结果为下一步建立飞机寿命资源存储量、消耗量、补给量之间的制约关系模型打下了基础。

[1] 戚燕杰,吕志刚,刘马宝. 寿命无极限：飞机寿命管理的技术革命[J]. 中国民航大学学报,2011,29(1)： 29-34.

[2] 杨茂胜,陈跃良,郁大照. 考虑飞行强度影响的飞机使用寿命综合评定方法[J]. 海军航空工程学学报,2007,22(2)： 257-260.

[3] 殷建新,宋智桃. 飞机结构腐蚀与使用寿命研究[J]. 海军航空工程学院学报,2005,20(6)： 623-626.

[4] 何宇廷. 飞机结构寿命包线的确定方法[J]. 空军工程大学学报(自然科学版),2006,7(6)： 1-3.

[5] Leung Y,Wu W Z,Zhang W X. Knowledge Acquisition in Incomplete Information Systems： A rough set approach [J].European Journal of Operational Research,2006,168(1)：164-180.

[6] 陈小玉,张静. 基于粗糙集-神经网络的变压器故障诊断方法[J]. 制造业自动化,2011,33(9)： 52-54.

[7] 王全,杨国梁. 一种改进的K平均聚类算法[J]. 国外电子元器件,2008,9： 73-74.

[8] 苗夺谦. Rough Set理论中连续属性的离散化方法[J]. 自动化学报,2001. 5： 296-302.

[9] Thangavel K,PethalakshmiA.Dimensionality reduction based on rough set theory： a review[H]. Applied Soft Computing,2009,9： 1-12.

[10] 吴德胜,梁墚. 遗传算法优化神经网络及信用评价研究[J]. 中国管理科学,2004,12(1)： 68-74.

[11] 焦李成. 神经网络系统理论[M]. 西安： 西安电子科技大学出版社,1992.

[12] Tushman M,L. Hybrid Neural-Network Genetic-Algorithm Technique for Aircraft Engine Performance Diagnostics[J]. 2005,21(4)： 42-45.