一种基于BUBBLE小波的焊缝检测技术
2012-04-10刘重阳徐毅华
刘重阳,徐毅华,张 磊
LIU Chong-yang1,XU Yi-hua1,ZHANG Lai2
(1. 兰州石化职业技术学院 电子电气工程系,兰州 730060;2. 兰州理工大学 电气工程与信息工程学院,兰州 730050)
0 引言
随着焊接技术的快速发展,它在生产建设中日趋广泛的应用,到目前已经成为一种重要的加工手段。焊缝自动跟踪是现代焊接技术的一个重要方面。尽管近年来焊缝跟踪技术得到了很大的发展,但由于焊接是一个非常复杂的过程,焊接过程中的工件的加工误差、电磁干扰、热变形等各种干扰因素的影响,是焊缝跟踪技术的研究成果的实用化进程非常缓慢,到目前为止,现场焊接生产中焊缝自动跟踪问题尚未得到满意的解决。精确的焊缝跟踪是保证焊接质量的首要条件,而准确地获取焊缝信息是精确的焊缝跟踪的前提。
目前提取焊缝信息的常用传感器有电弧式、机械式、温度式和光电式等传感器[1],其中由于视觉传感器可以远离强光和强热区,采集的信息量大,受到人们的青睐。但由于焊接过程中弧光、飞溅和烟尘等因素,使视觉传感器CCD摄像机采集到的焊缝图像信息有噪声干扰,如何去消除这些噪声干扰从而得到有用清晰的焊缝信息是保证精确的焊缝跟踪的关键。随着机器视觉、图像处理技术的发展,以及小波分析技术的出现和完善,为我们解决此类问题提出了一种新的方法。本文采用具有对孤立噪声有很强抑制的BUBBLE小波[2]对采集的原始焊缝信息进行边沿检测分析,并把二维的焊缝信息转换为一维的焊缝信号,以求得到更好的处理结果。
1 小波边缘检测技术
小波变换是时间(空间)频率的局部分析,它通过伸缩平移运算对信号(函数)逐步进行多尺度细化,最终达到高频处时间细分,低频处频率细分,能够自动适应时频信号分析的要求,从而可聚集到信号的任意细节。
1.1 小波边沿检测原理
设 Ψ ☒ L1☒ L2且 (0)= 0,则按下式生成的函数族 {Ψa,b}:

叫分析小波,Ψ叫基本小波。Ψ ☒ L1☒ L2且满足:
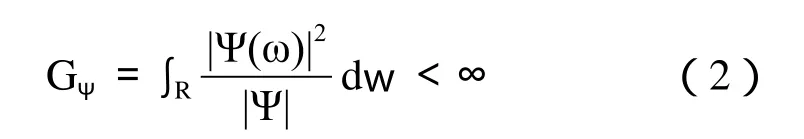
则Ψ叫做允许小波,式(2)称为允许条件。
式中:Ψ (ω)为Ψ (x)的傅立叶变换,x可以是时间也可以使空间变量。
在一般情况下,常选择具有紧子集或近似紧子集的并且具有正则性的函数作为小波母函数。紧子集意味着时域的局部性,而正则性意味着频域的局部性。
由可容性条件可知,Ψ (0)=0,所以小波母函数的直流分量为零,它呈现为正负交替的形状。尺度a的小波函数为。根据马莱塔的定义,任意f (x) ☒ L2(R),以Ψa(x)作为小波时的小波为f(x)和Ψa(x)的卷积。
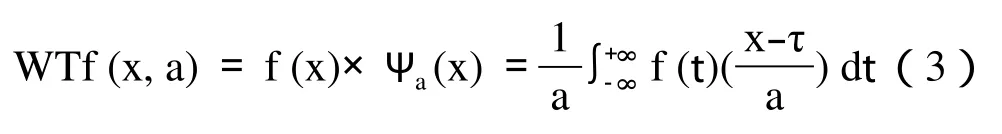
卷积在物理上的表现为滤波器对信号f (x)的滤波,滤波器的脉冲响应为Ψa(x)。
设θ (x)为一具有低通平滑作用的滤波函数:
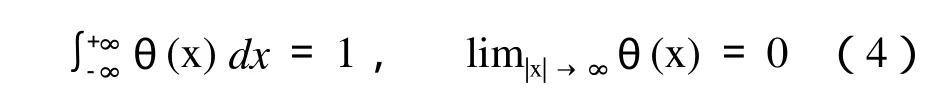
假设θ (x)具有一阶,可用ξ (x)表示,则:
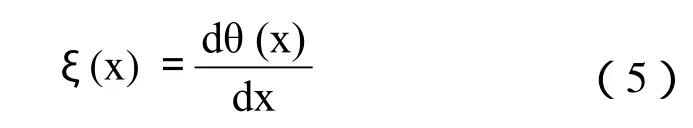
容易推知,ξ (x)满足可容性条件,所以ξ (x)可作为小波母函数。用ξa(x)和对f (x)坐小波变换,则有:
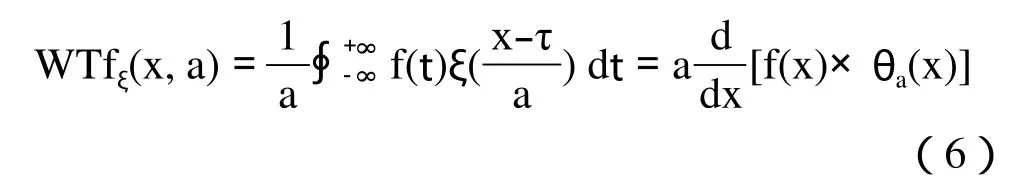
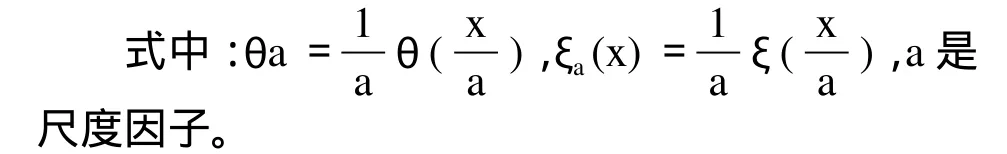
由式(6)可知,WTfξ(x,a)是 f(x)与θa(x)的卷积,也就是f(x)通过θa(x)滤波,再求其微分。由于θa(x)是一个平滑滤波函数,所以f (x)经过θa(x)滤波后,f (x)的噪声得到了抑制;而微分运算,反映了f (x)的变化率很大,当f (x)中存在边沿时,即突变点,它的变化率就很大,达到模极大值,所以WTfξ(x,a)取极值点的地方就是f (x) 的边沿位置,这就是基于小波变换模极大值进行边沿检测的基本原理[3]。
1.2 BUBBLE小波函数
一维BUBBLE小波函数为:
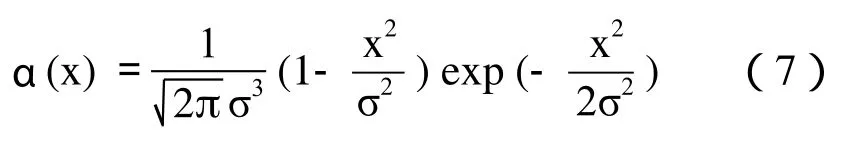
其傅立叶变换为:

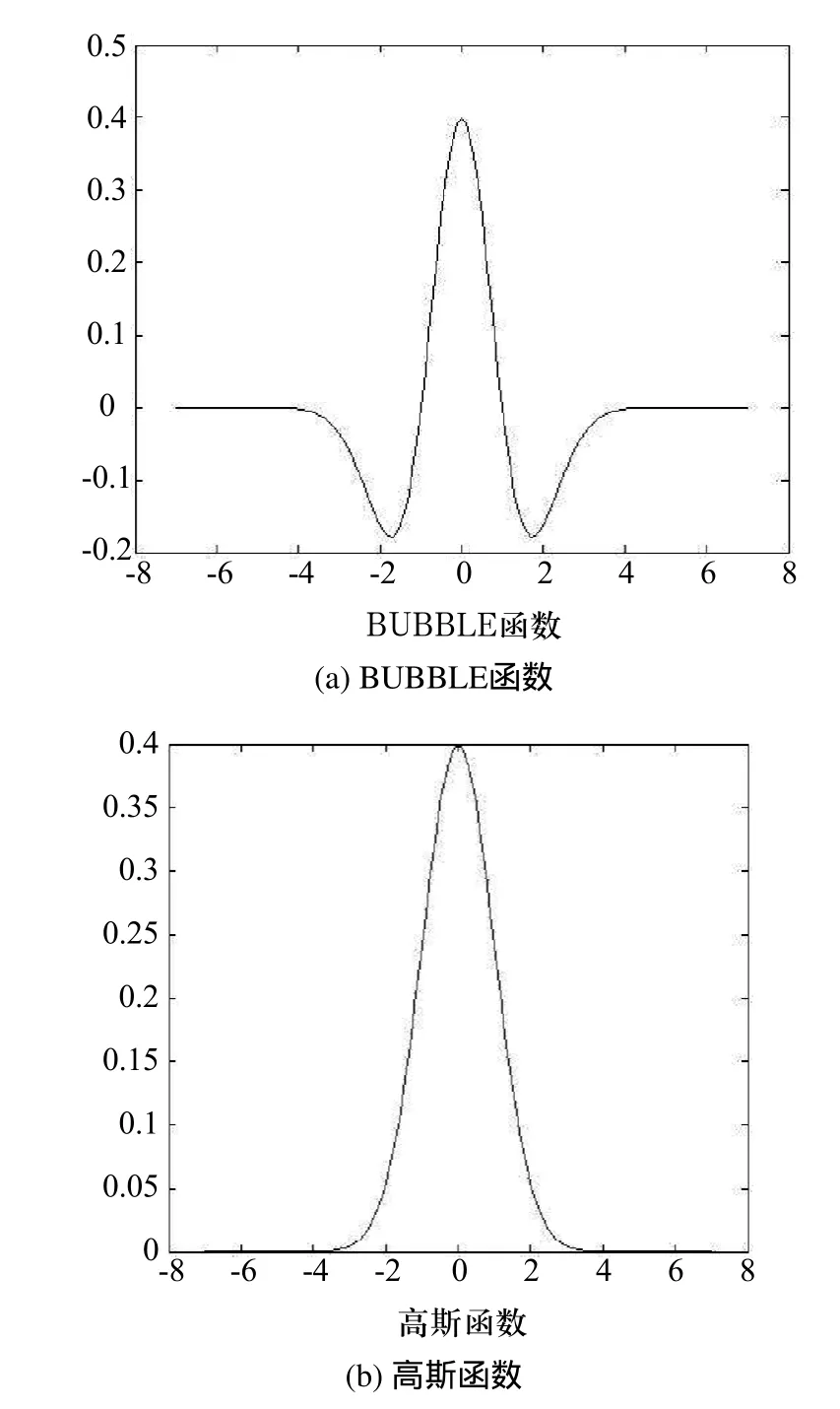
图1 BUBBLE小波函数和高斯函数
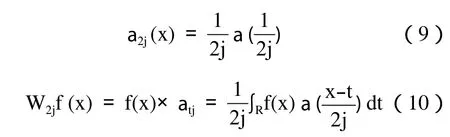
由于高斯函数是构成R空间V的基,为了应用马莱特快速算法,我们引进高斯函数(图1 (b))作平滑函数:

平滑函数的傅利叶变换为:

对于高斯函数有二进二次度方程:
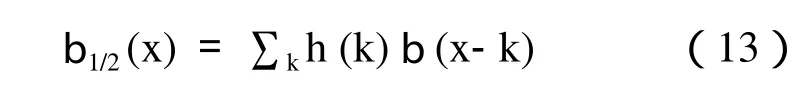
对上式两边作傅利叶变换:
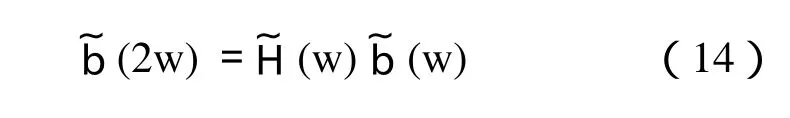
由于高斯函数是基,对于BUBBLE函数也有:
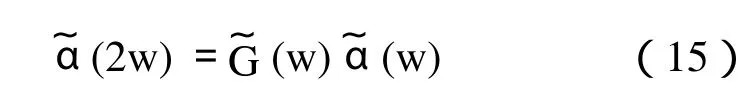
由式(8)、(14)和(15)可得:

则H(w)和G(w)的傅利叶反变化为:
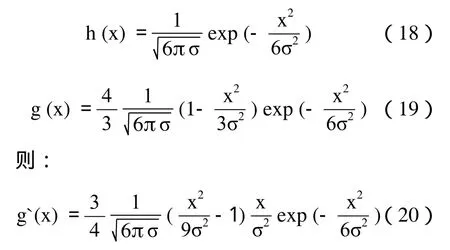
gσ(x)和 g`σ(x)的形状如图 2 所示。
一维BUBBLE小波函数可以用来检测一维信号突变点,BUBBLE小波的尺度参数取不同值,可以构照具有不同侧仰制性能的小波基。作者取σ=0.5,1,1.5,则通过式(19)、(20)可以分别得到3组一维离散滤波器系数,见表1。

表1 BUBBLE小波的一维离散滤波系数
2 焊缝信号的检测方法与仿真结果
2.1 检测方法
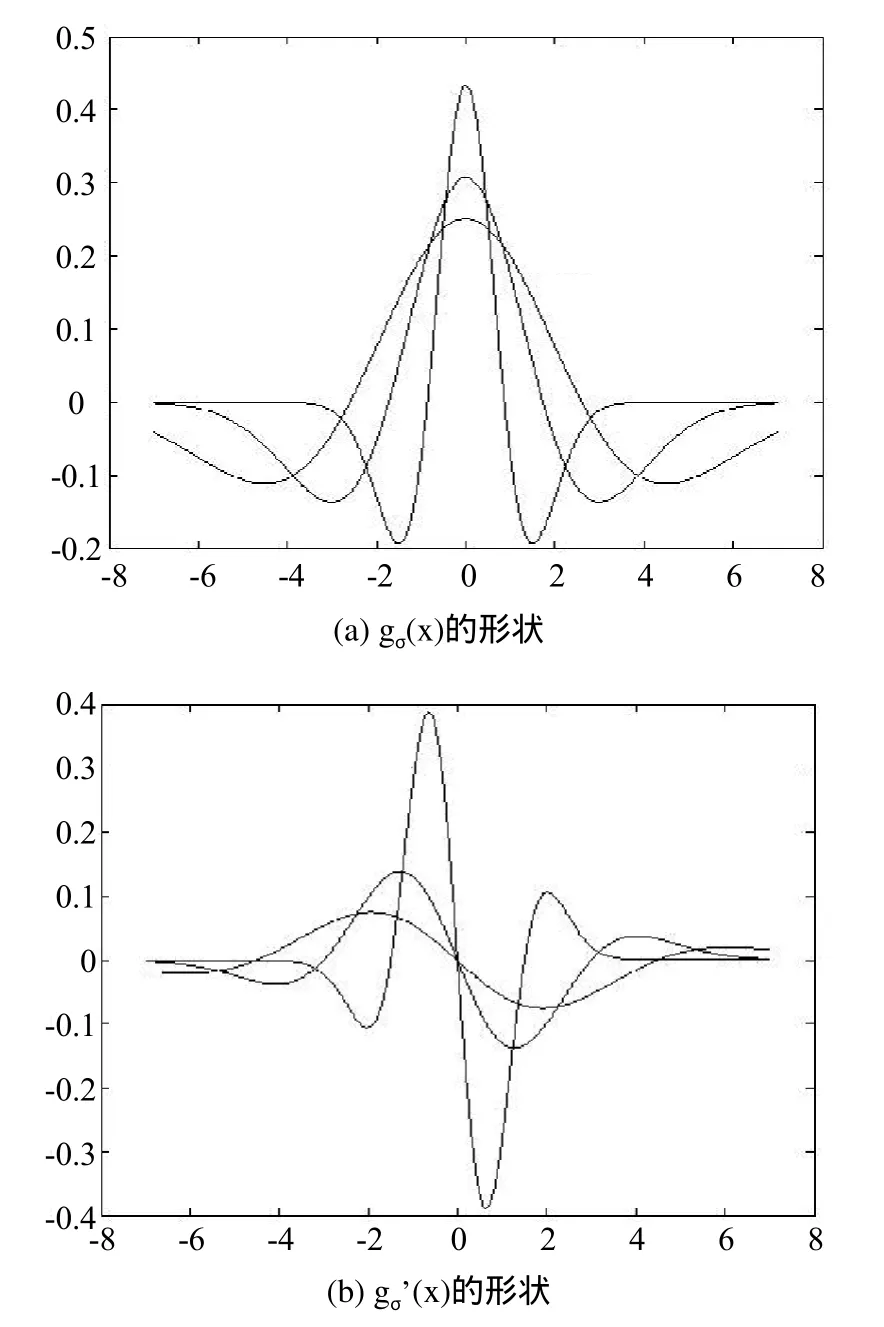
图2 BUBBLE小波的gσ(x)和gσ’(x)的
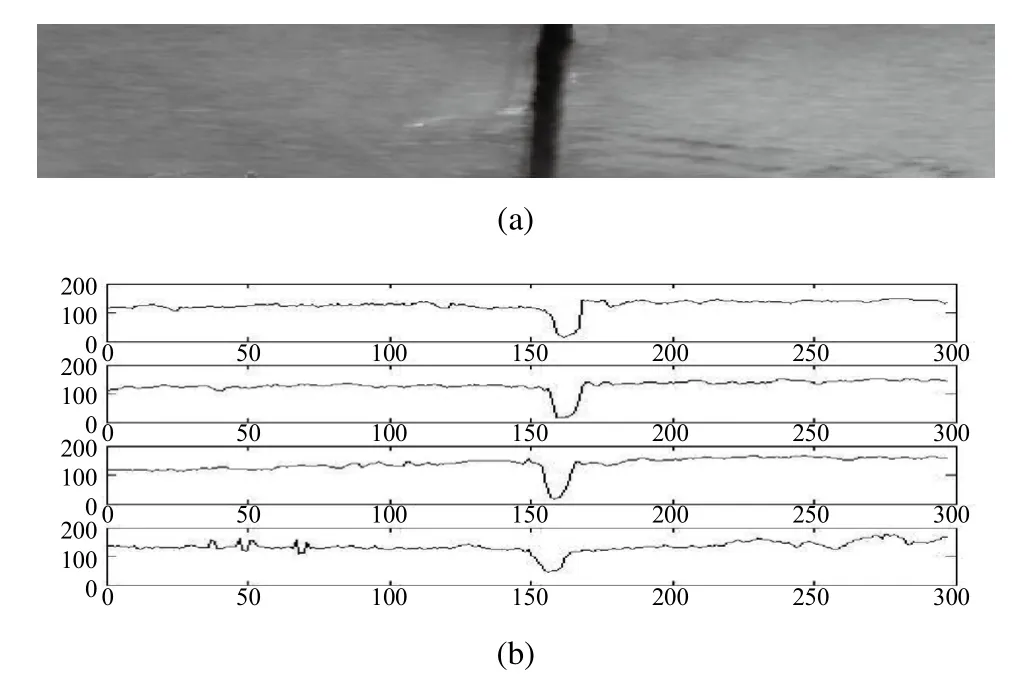
图3 某一帧内焊缝的图像
CCD摄像机采集的图像信号会因为现场的弧光的干扰、受焊的铁块生锈、烟尘等的影响,有叠加的强的不规则噪声。图3(a)是我们抓拍到的某一帧255灰度级的焊缝图像,图3(b)为不同位置点横截面上的灰度随机曲线。
由于在具体的焊接过程中,焊炬伴随着焊接机器人的焊接速度每走一步可近似为直线。所以图3中所给出的CCD采集到某一帧的焊缝图像,我们可以根据焊接速度以及矫正间隔时间,可以等分为若干段小间隔图象信号。从图3(b)中我们可以看到,焊缝信号是一个随机过程,这些曲线可看成为随机时间的多次取样或者实现。在此随机事件中的参变量为位置变量。对应每一个位置点,它的灰度值是一个随机变量,其取值空间为[0,255],概率分布服从正态分布,因而可以用样本的均值估计该随机变量的均值,即:

其中:f(a,b)为(a,b)位置的图像灰度值;a为垂直于焊缝方向的坐标;b为平行于焊缝方向的坐标;n为一帧内平行于焊缝方向的像素点数;x(a)为响应的一维信号。这样我们根据上述分析把图3(a)所显示的焊接中某一帧焊缝的原始图像分为近似的四段,把一幅二维的图象转为四个一维信号,通过转换为对一维信号的分析进行焊缝的边缘检测。如图4 所示为四个一维的焊缝信号形状。
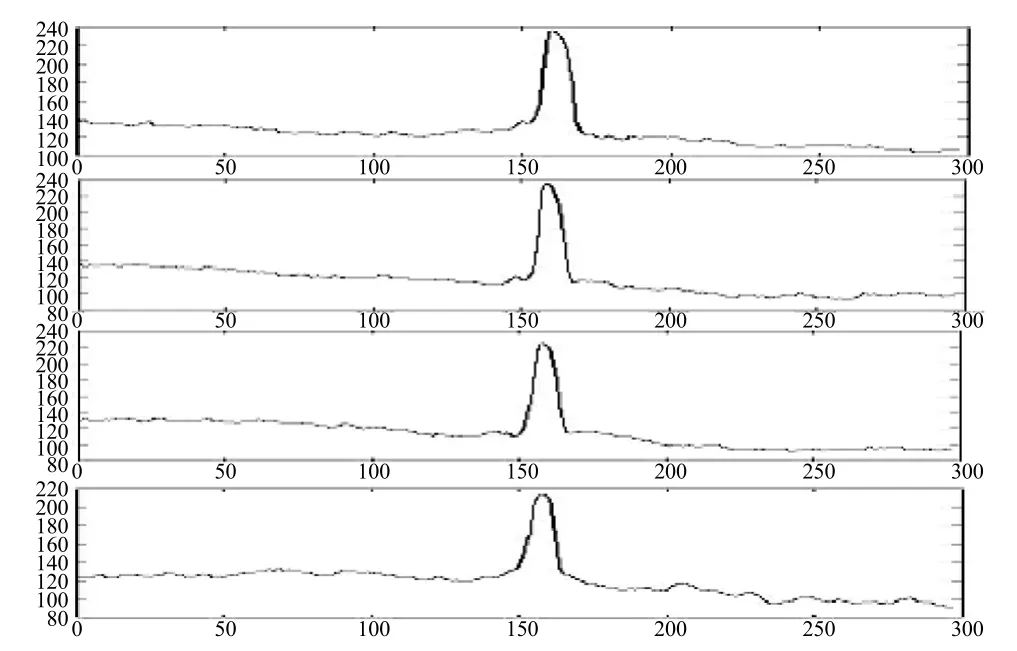
图4 一维焊缝信号
2.2 仿真结果
图4 显示焊缝经一维转换处理后表现为”屋脊”形,表现为由一个上升沿和另一个下降沿构成[4]。上升沿经过小波变换后,表现为极大值;下降沿经过小波变换后,表现为极小值;则焊缝位置就是取极大值与极小值之间。由式(7),对一维焊缝信号x(n)的小波变换,可以用离散的α(n)与x(n)进行数字卷积来代替。但是为了避免信号卷积运算带来的信号边界的延拓问题,有必要对原始信号数据进行延拓。延拓部分数据长度直接与滤波器长度有关如滤波器长度为N,则需要延拓(N/2)点数据。
具体的需延拓长度表达式为:
如N为偶数,则延拓长度d=N/2;
如N为奇数,则延托长度为d=(N-1)/2。
本文采取线形延拓[5],因其方法产生的误差较小。信号延拓部分的数据通过对信号延拓端数据线形拟合得到。原始信号x(m)经过延拓后成为:

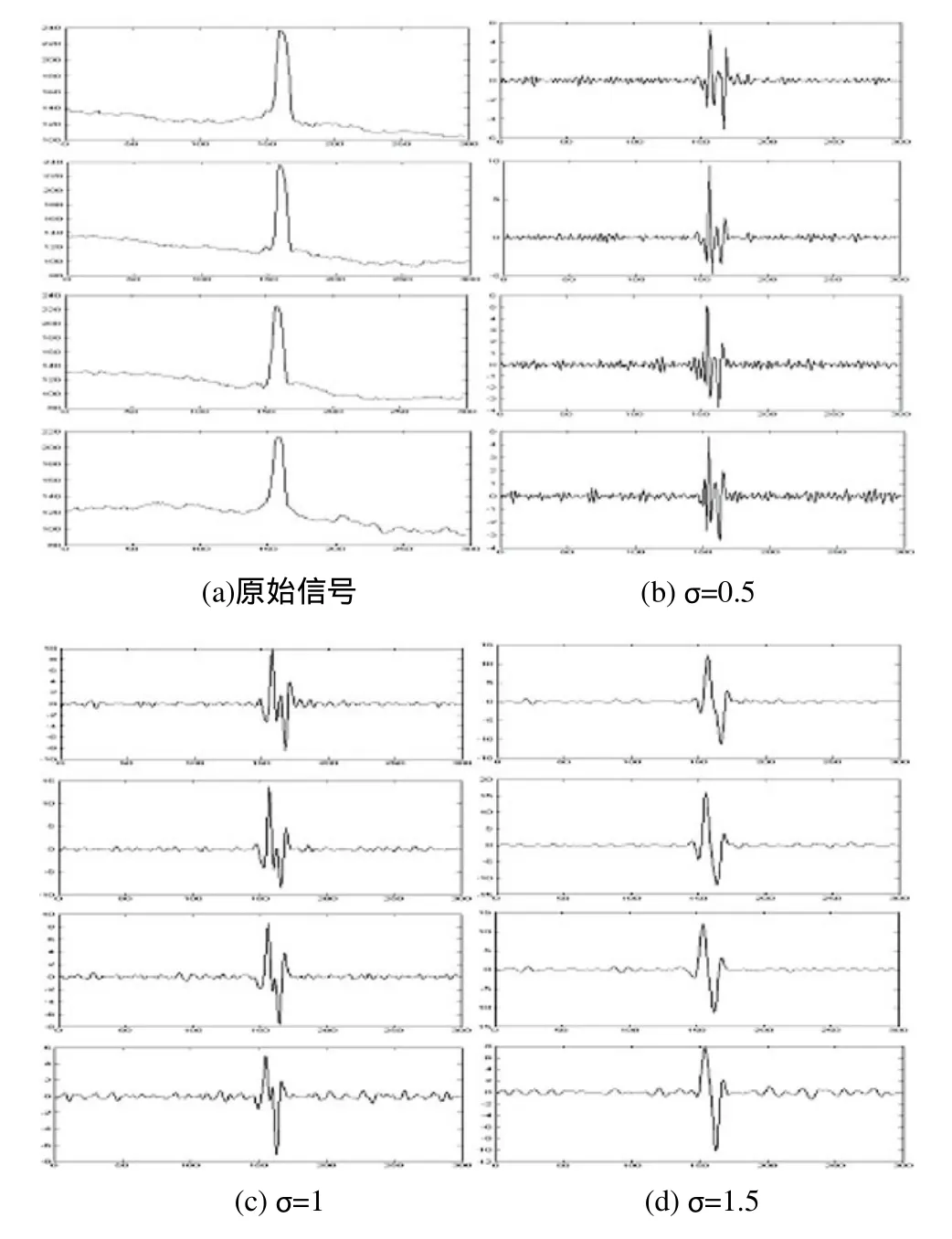
图5 原始信号与不同尺度σ下的仿真结果
更一般得表达式,如果信号断点数据为x(a),x(a+1),对信号左端进行延拓,其值为:
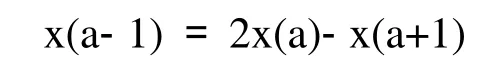
对信号右端进行延拓,其值为:

设x(m)为有限信号,长度为M,经线形原拓后为信号X(m)。X(m)经过长度为N的滤波器滤波后,输出:
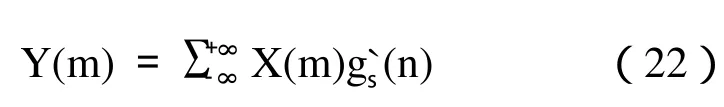
取 Y(m)信号的主值 y(m),m ☒ [0,M-1],作为x(m)滤波后的输出。
图5所示为连续几帧焊缝图像的仿真结果。图5.a为小波变换前的焊缝一位平均原始信号,从图中可以看到焊缝的“屋脊”特性比较明显,其它位置的噪声得到一定程度的抑制。事实上,对采样值求平均也是一种低通滤波算法。图5(b)、(c)、(d)为图5(a)信号在不同尺度σ下的小波变换结果。从图5中可以看出,在σ=1.5时,得到的小波变换效果最好;在σ=0.5时,噪声未有得到抑制却有点加强;σ=1时,虽然噪声得到抑制,滤波效果已经较好,但有时会出现大的起伏,对于真正的极值点的检测造成影响。表2分别给出了检测的结果,位置点是用像素数(pixel)表示,并且列出了与实际测量之间的误差大小。
3 结束语
采用基于BUBBLE小波变换检测技术能够有效地抑制噪声的影响,提高了检测的准确度。并且采用把二维的焊缝原始图像信号通过平均值的转化为一维的信号,即起到了很好的滤波的效果,也有降低了计算量以及程序的处理速度。同时通过对不同尺度σ的分析,从仿真的结果中得出在尺度σ=1.5是效果最好的;并且使用线性延托法有效地去除了卷积过程带来的信号伪边缘的影响。
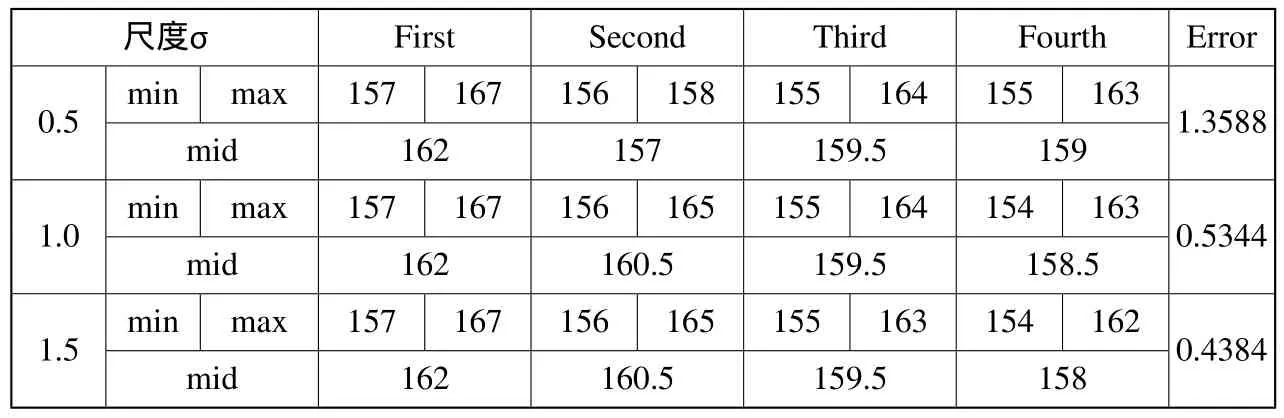
表2 不同尺度σ下检测点与误差
[1] 侯晓峰. 焊缝自动识别与跟踪. 哈尔滨工程大学硕士论文[D]. 2004.
[2] 朱宏擎,林良明,等. 基于BUBBLE小波的结肠镜图像暗区中心点估计的研究. 中国生物医学工程学报[J]. 2002,10(5): 437-442.
[3] 屈稳太,诸静. 基于Gauss小波的焊缝检测技术[J]. 焊接学报,2002,8(23): 64-68.
[4] 杨恒,杨方海,梁德群. 多尺度边缘检测中的有效尺度研究[J]. 电子与信息学报,2001,23(1): 1-8.
[5] 袁礼海,宋建社. 小波变换中德信号边界延拓方法研究[J]. 计算机应用研究,2006,23(3): 25-27.
