微地形对输电线路舞动的影响

景乾明，胡春梅，胡基才，张承学

(1.甘肃省电力公司，兰州市， 730050;2.天水超高压输变电公司，甘肃省天水市， 741000; 3.武汉大学，武汉市， 430072)

0 引言

覆冰输电导线在一定冰风条件下所诱发的舞动是一种低频、大振幅的自激振动［1］。导线舞动容易导致系统短路和连续跳闸、导线烧伤、断股和断线、各种线路金具以及杆塔的损坏［2］。随着我国电网覆盖面的不断扩展以及电压等级的不断提高，穿越复杂地形及恶劣气候条件的送电线路日益增多［3］。由于山区尤其是高海拔山区的局部特殊地形地貌不同，使得其局部气象具有明显的立体特征，即使在一个小范围内，不同地形的局部气象指标也存在极大的差异［4］。这些差异将直接导致多变的局部气流条件和不同的导线覆冰［5］，使得按一般条件所设计的输电线路在这些地区会经常产生严重舞动，造成巨大的工程事故隐患。由于导线舞动的复杂性和特殊性，使用计算机仿真技术研究不同地形地貌条件下的导线舞动具有特殊优势。目前国内外对导线舞动的仿真研究还处于起步阶段，而运用计算机仿真技术对微地形条件下的导线舞动研究较少［6］，因此采用仿真技术研究微地形条件下的输电线路舞动具有重要意义。

1 微地形及其对空间流场的影响

微地形对输电线路舞动的影响主要体现在2个方面:影响局部空气流场和导线覆冰。

1.1 微地形对空间流场的影响

甘肃电网某330 kV线路的66～67档位于一个峡谷山坡的顶部附近，2杆塔导线悬挂点的高差约为40 m。特殊的地形地貌将直接改变导线周围的空间流场，包括风速、风向和气流性质等。利用计算流体力学软件可以建立相应的流场模型。图1为由计算机仿真计算所求得的该微地形条件下的空间流场分布。

计算结果表明，当风速为15 m/s的水平层流风经过该微地形时，风场产生了严重的紊流现象。在导线截面所在的不同空间位置，各点的风速和风向均与入口处不同。覆冰导线中点处的实际风速约为21 m/s，而风向与水平面的夹角约为15°。

图1 微地形附近流场截面Fig.1Cross section of flow field near the micro-terrain

1.2 微地形对导线覆冰的影响

微地形导致导线周围风速、风向等发生改变，从而影响到导线的覆冰。一般导线的覆冰与导线接触过冷却水滴的有效面积相关，导线迎风面冻结相对较大，而背风面则相对较小;同时冰结厚度与风向和导线之间夹角的正弦成正比，即当风向垂直于导线轴线时冻结厚度增长最快［7］。此外，导线的覆冰还与导线结构、温度、海拔、大气湿度、气压等因素有关［8］。

根据图1所示的流场计算结果以及对该档线路的实际观测，该档线路的实际覆冰形状为雾凇性质的D型覆冰。

2 导线舞动的仿真模型

2.1 导线动力学模型

考虑竖直位移、水平位移和扭转位移3个自由度，建立覆冰导线三自由度集中参数动力学模型［9］，如图2所示。

图2 三自由度集中参数系统模型Fig.23-D lumped-parameter system model

对图2所示模型建立其垂直(y向)、水平(z向)及扭转振动的综合动力学运动方程［10］为

式中:U为风速;D为导线迎风尺寸;ρ为空气密度; α为攻角;为扭转振动的角速度和角加速度;y和z为竖直和水平自由度;为竖直、水平方向的速度及加速度;CL、CD、CM为升力、阻力、扭矩系数;Cy为Y向空气动力系数;ξy、ξz、ξt为模型在3个方向上的结构阻尼率;ωy、ωz、ωt为模型在3个方向上得振动固有频率;ky、kz、kt为模型在3个方向上的刚度;mi为单位长度导线上的覆冰质量;β0为初始凝冰角;r为导线半径;R为特性半径，本文可取为半径r。

2.2 导线构型

导线的构型方程［11］为

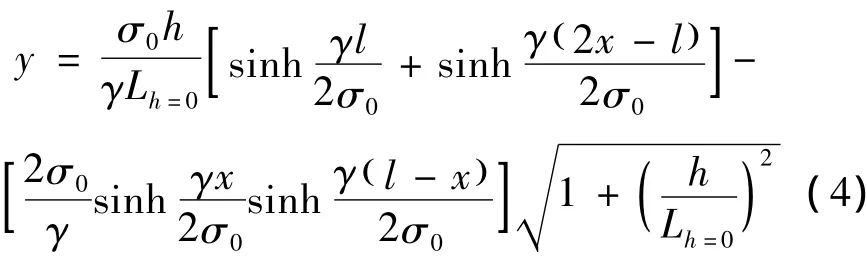
式中:x为导线上某点与左悬挂点的水平距离;y为导线上某点与左悬挂点的垂直距离;l为档距;γ为单位长度与截面积上承受的载荷;σ0为导线水平应力;h为悬挂点高度差;Lh=0为两侧悬挂点等高时档内悬链线的总线长，Lh=0=(2σ0/γ)sinh(rl/2σ0)。

3 微地形下的导线舞动及仿真分析

二分裂330 kV线路66～67档的结构参数如下:档距为203 m;两杆塔绝缘子海拔差为39 m;导线型号为LGJ300/ 40;平均运行张力为10.096 kN。

对该线档进行模态分析［12］，求得该系统前4阶固有频率结果如表1所示。

表1 前4阶固有频率Tab.1Natural frequency of fourth-order

在2011年2月的实际观察中，发现该档导线发生舞动，舞动振型为二阶振型，舞动振幅的最大峰峰值约为3 m。现场观测该档导线为D型覆冰，覆冰厚度为10 mm，现场平均风速约为15 m/s。

3.1 考虑微地形影响的仿真计算

根据该档线路实际微地形条件，建立导线系统的有限元模型，并利用所开发的“输电导线舞动仿真计算平台系统”进行动力学仿真计算，计算结果如图3所示。

图3 考虑微地形的仿真计算振型Fig.3Vibration mode of the simulation calculation with micro-terrain

图4为距左塔50 m处的Y向振动时间历程仿真曲线及频谱图，导线在600和1 200 s时的截面舞动轨迹如图5所示。

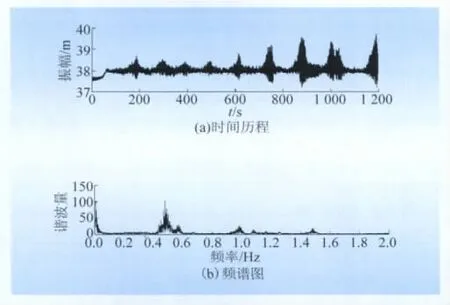
图4 Y向振动时间历程及频谱图Fig.4Time history and spectrogram of the vibration in Y direction

从图3、4的仿真结果可以看出，该档导线舞动过程中Y向的最大振幅约为2.7 m，发生在距左塔50 m处，与图4的实际观测结果相近。该档导线的Y向振动是主频约为0.45 Hz的二阶振动，这与表1的理论分析十分接近，也和所观测到的二阶舞动现象一致。

从图5的仿真结果可以看出，导线在舞动过程中的截面轨迹大体上为一斜椭圆状，与导线舞动的理论分析结论相一致［1］。

图5 导线舞动的轨迹曲线Fig.5Locus curve of the conductor galloping

上述分析表明，该仿真结果在舞动模态、舞动振幅以及舞动轨迹方面均与理论分析和实际观测基本相符，这表明该计算机仿真平台系统所得的仿真结果可信度较高。

3.2 忽略微地形影响的仿真计算

如果忽略该处的微地形结构，即认为该档导线只是位于海拔不同的2个山坡上，在相同的水平风速、相同的覆冰厚度、相同的线路结构的前提下，运用同样的方法对该档导线系统进行动力学仿真计算，结果如图6所示。

图6 忽略微地形的导线舞动振型Fig.6Vibration mode without micro-terrain

从图6可以看出，不考虑微地形条件下导线的舞动振型为一阶振型，舞动振幅最大处位于档距中点附近位置，最大振幅约为5 m。此时档距中点处的Y向振动时间历程和频谱图如图7所示，导线中点在600和1 200 s时的截面舞动轨迹如图8所示。

图6、7的仿真结果表明，此时该档导线舞动过程中Y向的最大振幅约为5 m，发生在档距中点处。此时该档导线的Y向振动主频约为0.22和0.45 Hz，这与表1中导线的一阶固有频率0.21 Hz和二阶固有频率0.42 Hz接近。表明导线同时存在一阶和二阶振动成分，同时由于一阶舞动的振幅大于二阶舞动的振幅，所以导线的振型包络线主要呈现为一阶的形状。

图8的仿真结果表明，此时导线在舞动过程中的截面轨迹更接近理论上的椭圆状，这是由于忽略了微地形后，系统所在的流场和流场作用在导线上的外载荷都更加均匀所致。

图3～8之间的对比表明，微地形的考虑与否对导线舞动的模态、振幅以及截面轨迹等有着显著的影响，因而将对线路系统的结构设计、防舞设计、强度计算以及疲劳寿命评估等带来显著影响。

4 结论

(1)在理论分析的基础上，建立了覆冰导线的三自由度分析模型和有限元计算模型，并对某实际档距进行了实际仿真计算。仿真计算结果不仅与理论分析相符，而且与实际舞动观测结果相近，表明该分析模型和仿真计算可信。

(2)利用计算流体动力学仿真软件建立了某实际线路微地形结构的流场仿真计算模型，并进行了仿真计算。计算结果表明微地形对风速和风向都有不同程度的影响，而且依地形变化程度的不同相异较大，实际处理中应根据线路实际情况分析求解。

(3)影响输电导线覆冰的因素很多，应当综合考虑。微地形导致导线周围流场的变化对输电导线的覆冰形状、覆冰方向、覆冰厚度以及覆冰过程都有显著的影响，但在实际处理中要具体情况具体分析。

(4)实际线路的仿真计算表明，微地形不仅对导线的舞动振幅和截面运动轨迹有较大的影响，而且还可能影响到导线的舞动振型。

(5)微地形对导线舞动影响的结论为线路设计部门和线路运行管理单位在线路的设计和防舞设计时提供了有益的指导。结论表明针对不同的地形地貌和气候条件，在进行线路设计时应慎重选择线路的走向并分别采用不同的档距等结构参数;对运行中有舞动隐患的线路在进行防舞改造设计时，应针对性地采取不同的防舞方案设计和参数设计。

［1］郭应龙，李国兴，尤传永.输电导线舞动［M］.北京:中国电力出版社，2002.

［2］沈峦峰，巫世晶，王晓笋，等.基于扭振激发机理的输电导线新型防舞模型［J］.电力建设，2010，31(3):34-37.

［3］王守礼，张弦.微地形微气象对输电线路的影响及响应措施［J］.云南电业，2005(6):36-37.

［4］Zhou Q，Yang Z S，Chen W G． Design of conductor galloping multipoints monitoring system using ZigBee PRO wireless network technology［J］． High Voltage Engineering，2011，37( 8) : 1967-1974．

［5］蒋兴良，周仿荣，王少华，等.输电导线覆冰舞动机理及防治措施［J］.电力建设，2008，29(9):14-18.

［6］严波，胡景，周松，等.覆冰四分裂导线舞动数值模拟及参数分析［J］.振动工程学报，2010，23(3):310-315.

［7］魏其巍.电线覆冰机理分析及在工程设计中的应用［J］.电力建设，2007，28(3):26-28.

［8］金西平.微地形微气候对电力线路覆冰的影响［J］.供用电，2008，25(4):17-20.

［9］李欣业，张华彪，高仕赵，等.三自由度模型覆冰输电导线的数值仿真分析［J］.河北工业大学学报，2010，39(3):1-5.

［10］李黎，陈元坤，夏正春，等.覆冰导线舞动的非线性数值仿真研究［J］.振动与冲击，2011:30(8):107-111.

［11］石端伟.机械动力学［M］.北京:中国电力出版社，2007.

［12］Li L，Chen Y K，Xia Z C.Nonlinear numerical simulation study of iced conductor galloping［J］.Journal of Vibration and Shock，2011，30(8):107-111.

(编辑:张磊)