输电线路窄基铁塔基础抗倾覆公式

吴炯，汪梅，程东华

(1.银城地产集团，南京市，210000;2.南京长江都市建筑设计有限公司，南京市，210002; 3.佛山电力设计院有限公司，广东省佛山市，528200)

0 引言

在输电线路基础工程的设计中，窄基铁塔基础(简称窄塔基础)通常作为钢管杆或窄塔的基础型式，用以抵抗上部结构传递的较大水平力和倾覆力矩。由于该类基础的破坏机理复杂，加之关于此类基础的研究数据较少，导致对该类基础的设计过于保守。近年来，随着国家电网公司“两型三新”线路设计建设导则的进一步推广和实施，输电线路基础的设计理论越来越受到研究学者和工程师的重视。完善输电线路窄塔基础的设计理论，对于节约资源，减少基础占地面积，进一步优化输电线路基础设计有着重要的意义。

关于窄塔基础倾覆稳定计算的依据，一直以来都是沿用《架空送电线路基础设计技术规定》［1］(简称《规定》)中的相关计算公式，近年来，部分研究人员对此亦做了相关研究。文献［2］采用地基反力系数法，对刚性短桩基础沿地表面的变位进行了分析，文献［3］对窄基铁塔倾覆稳定的计算方法进行了探讨;国外的一些研究人员［4-5］对钢管杆或者窄塔基础进行了现场试验，结果表明，回填土的密实度和基础埋深是影响基础抗倾覆稳定的主要因素。

本文重新推导了窄塔基础的抗倾覆公式，将推导公式得到的结果与有限元模拟的结果进行了对比分析，较好地解决了原公式中存在的一些问题。

1 窄塔基础抗倾覆稳定的分析方法

因上部结构和荷载工况的特殊性，输电线路窄塔基础承受着较大的水平力和倾覆力矩，所以该类基础尺寸及埋深往往由倾覆力矩的大小和基础的容许变位控制。窄塔基础倾覆稳定的分析方法包括有限元分析法、极限平衡法、地基反力系数法等。其中，极限平衡法因受力图式简便、计算思路明确以及计算所用的土性参数较少等优势，被广泛应用于工程设计中。

用极限平衡法分析基础的倾覆稳定有2种思路: (1)通过条件假设和力学模型的简化，确定基础在极限倾覆状态下的土反力的分布和倾覆转动中心，然后以转动中心为矩心，通过静力平衡条件分别求出极限倾覆状态下的抗倾覆力矩和实际受力状态下倾覆力矩，通过定义安全系数来确保基础的安全;(2)根据假设的基础倾覆破坏模式，对造成基础倾覆的水平力引入水平力分项系数，然后在基础的极限倾覆状态下，求出抗倾覆力矩与倾覆力矩。为保证基础的安全，抗倾覆力矩必须大于等于倾覆力矩［6-11］。《规定》采用了第2种方法验算窄基铁塔的倾覆稳定。

2 输电线路窄塔基础抗倾覆公式

根据《规定》中的窄塔基础抗倾覆简化计算公式及其说明，可将公式的左项认为是外力实际作用下的倾覆力矩M外;公式的右项可视为基础在极限状态下的抗倾覆力矩Mu。当M外＜Mu时，基础处于安全稳定的状态。在实际输电线路工程的设计过程中，当基础在特定的某个埋深并处于某种受力工况条件下时，通过《规定》中的公式计算所得到的Mu有可能出现负值的情况，工程设计人员对于该种情况很难解释，继而也制约了基础抗倾覆公式的应用;基于以上问题，本文进行了如下探讨。

2.1 窄塔浅基础抗倾覆简化计算公式

图1为浅基础倾覆计算受力简图［3］。

图1 浅基础倾覆受力简图Fig.1 Overturning force of shallow foundation

当基础处于极限状态时，假定基础底板中心为倾覆转动点，基础的基底反力零点位于基底边缘处，基底反力分布呈三角形分布。基础周围土体的极限土压力仍然采用朗肯被动土压力公式进行计算。有台阶浅基础和无台阶浅基础的倾覆稳定计算简图分别如图1(a)和图1(b)所示。图1中，O点为基础的倾覆转动点。

2.1.1 有台阶浅基础令E=ma0ht2/2，θ=h1/ht，则主柱的土压力

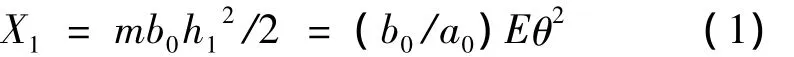
式中:m为土压力参数;a0为底板侧面计算宽度，m; ht为基础埋深，m;b0为主柱侧面计算宽度，m;h1为主柱埋深，m。

台阶处的土压力

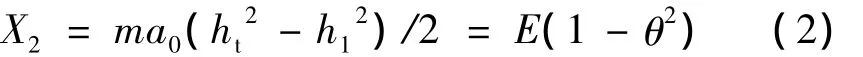
基础地基反力

式中:F为上部结构的竖直作用力，kN;G为基础自重，kN;γf为基础附加分项系数;S0为上部结构水平作用力，kN;fβ为地基与基础间的摩擦系数。

水平方向的力对O点的抗倾覆力矩

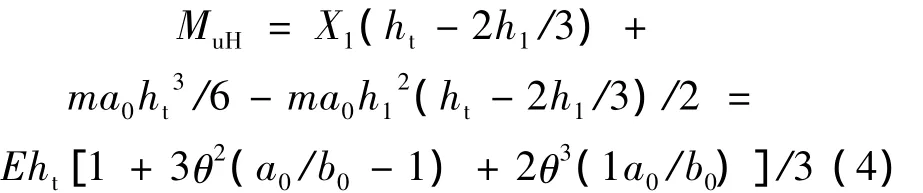
竖直方向的力对O点的抗倾覆力矩

式中:a1为底板正面计算宽度，m;b1为主柱正面计算宽度，m;e为基底反力的偏心距，m;y为基底向上的作用力，kN。

极限抗倾覆力矩

有台阶浅基础的倾覆稳定验算公式为

2.1.2 无台阶浅基础

无台阶浅基础型式的倾覆稳定验算公式为

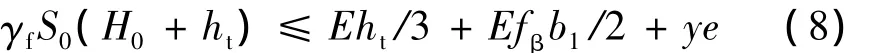
2.2 窄塔深基础抗倾覆简化计算公式

假设无台阶深基础型式的倾覆转动点为基础中心的某点处，而有台阶深基础型式的倾覆转动点位于基础台阶上表面的中心处。地基压力分布和基础周围土体的土压力计算均与2.1节相同。有台阶和无台阶深基础的倾覆稳定计算简图分别如图2(a)和图2(b)［3］所示。其中，O点为假定的基础倾覆转动点。

2.2.1 有台阶深基础

E和θ的取值与式(1)相同，X1、X2、y的计算公式分别同上述式(1)～(3)，则水平方向的力对O点的抗倾覆力矩

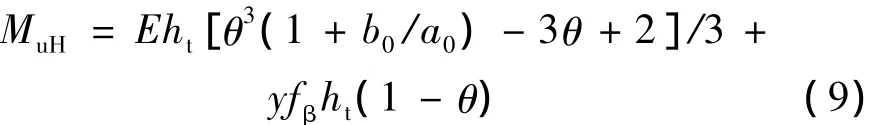
竖直方向的力对O点的抗倾覆力矩的计算公式同式(5)。

则有台阶深基础型式的倾覆稳定验算公式为

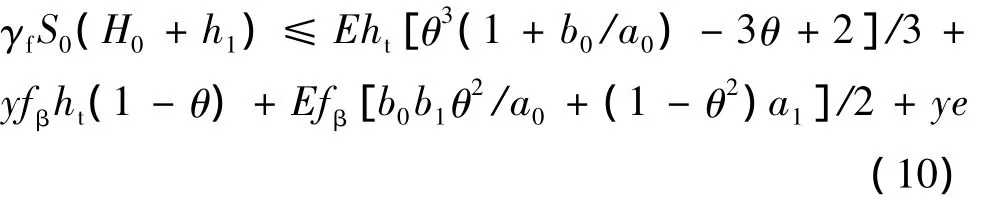
2.2.2 无台阶深基础

令E=mb0ht2/2，θ值与式(1)相同。

主柱的土压力

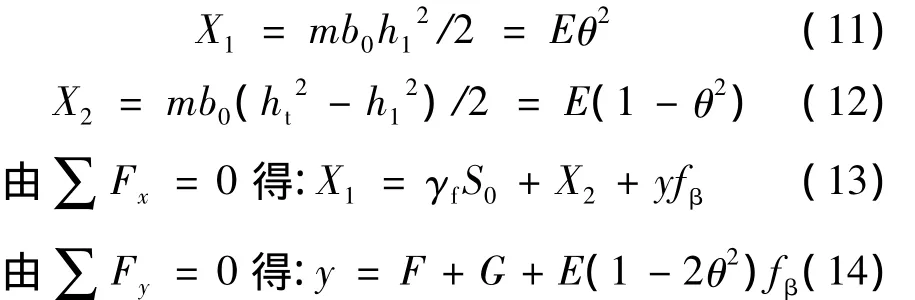
联立式(13)、(14)可得:

则无台阶深基础型式的倾覆稳定验算公式为

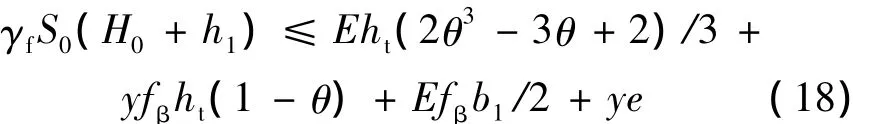
3 算例分析与有限元数值模拟

某高压输电线路工程窄塔基础的具体参数见表1，地基为均质土，无地下水，其中基础为方形基础。

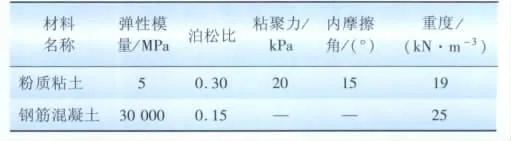
表1 有限元模型参数表Tab.1 Parameters of finite element model

设计初定基础尺寸为a=2 m，b=1 m，水平力S0=39 kN，竖直力F=100 kN，fak=200 kPa。

为了验证上述推导的抗倾覆公式的合理性，采用有限元分析软件对不同埋深下的无台阶基础和有台阶基础分别进行倾覆数值模拟分析，求出每种工况下的极限抗倾覆弯矩，并与本文推导的抗倾覆公式的计算结果进行了对比与分析。

在数值分析中，土体的本构采用Mohr-Coulomb弹塑性模型。基础与土体之间设置接触面，接触面满足库仑摩擦模型，钢筋混凝土假设为线弹性模型。

考虑有限元运行时间成本，同时为保证数值计算结果的合理性，本文在基础与周围土体的接触处布置了较密的网格，确保基础与土的相互作用;而远离基础的土体区域划分较为稀疏。有台阶基础模型及土体模型的网格划分如图3所示，其中图3(a)为基础及土体模型的网格划分示意图，图3(b)为基础与土体表面的网格划分示意图。

图3 三维有限元模型网格划分Fig.3 Mesh generation for 3D finite element model

通过有限元方法分析得到的基础抗倾覆弯矩与用本文推导的公式计算得到的结果对比如图4所示。

由图4可知:(1)随着埋深的增加，基础的抗倾覆弯矩呈非线性增加，并且通过公式计算不会出现负值的情况;(2)对本算例而言，埋深3 m处是划分浅基础和深基础的分界点，采用本文公式计算的抗倾覆弯矩在分界点处仅有较小的数值跳跃;(3)采用本文推导的公式计算得到的Mu-ht曲线变化趋势与用有限元法得到的基本一致，且Mu值留有一定的余度。推导公式计算的有台阶基础的抗倾覆弯矩偏小，这可能与忽略台阶上侧土体作用等因素有关。

图4 Mu－ht曲线图Fig.4 Mu－htCurve

4 结论

(1)随着埋深的增加，基础的抗倾覆弯矩呈非线性增长。

(2)当基础的埋深达到浅基础和深基础的分界点的深度时，本文推导的公式在分界点处计算的抗倾覆弯矩差值较小。

(3)基础的倾覆转动点位置以及浅基础和深基础分界点的划分都与土体的性质、土体和基础的相对刚度、基础的尺寸和荷载性质等因素有关，由于试验和理论研究资料的缺乏，这些问题还需要进一步深入研究。

［1］DL/T 5219—2005架空送电线路基础设计技术规定［S］.北京:中国电力出版社，2005.

［2］唐国安.对刚性短桩基础抗倾覆设计方法的探讨［J］.电力建设，1997(10):25-28.

［3］王开明，李喜来，尹鹏，等.窄基铁塔倾覆稳定计算方法的探讨［J］.电力建设，2010，31(4):9-12.

［4］Haldar A，Prasad Y V，Chari T R.Full-scale field tests on directly embedded steel pole foundations［J］.Can.Geotech，2000，37(2): 414-437.

［5］McNames C.Transmission pole foundations:alternate design methods for direct-embedded round，wood transmission poles［J］.Electrical Transmission and Substation Structures，2009(5):1-14.

［6］胡玉银.挡土墙抗倾覆稳定性分析［J］.同济大学学报:自然科学版，1995(3):321-325.

［7］余雄飞.地基软硬程度与挡土墙倾覆稳定性［J］.岩土工程学报，1998(3):94-96.

［8］王成华，郑虹.水泥搅拌桩挡土墙倾覆机理复杂性分析［J］.岩土工程界，2002(4):50-54.

［9］王刚，陈杨，张建民.大圆筒结构倾覆稳定分析的有限元法［J］.岩土力学，2006(2):238-241.

［10］吴鸿军，卢雯，马宏建，等.带立柱浅基础侧向极限承载力探讨［J］.铁道科学与工程学报，2008(3):73-77.

［11］曾革，周志刚.公路挡土墙抗倾覆稳定性设计方法［J］.中南大学学报:自然科学版，2009(4):1154-1158.