中小城市规划区高程异常模型建立

何德平，王艳茹

（重庆市勘测院，重庆400020）

中小城市规划区高程异常模型建立

何德平，王艳茹

（重庆市勘测院，重庆400020）

引言

“十一五”期间重庆市建成了覆盖全市域的重庆市连续运行卫星定位网络服务系统（简称CQCORS），该系统是集现代卫星定位、计算机网络、数字通讯等技术于一体的多方位服务和多领域应用的多功能系统；它由GPS参考站、数据处理与管理中心、数据通信网络和用户发布网络组成，它是“数字重庆”信息化建设的主要基础工程和重要的空间基础设施之一。

为了推动重庆市连续运行卫星定位网络服务系统在区县中小城市的应用，满足重庆区县城市规划建设需要，应解决WGS-84坐标系统向区县地方坐标系和高程系统转换的问题，需建立区县城市规划区高程异常模型，实时获取区县城市规划区地方坐标系统和高程系统成果。

1 某区城市规划区已有资料情况

在某区城市规划区已布设了1个A级GPS连续运行参考站，1个B级GPS点，5个C级GPS点，20个D级GPS点，100个一级导线点，均有精确的平面和高程成果。由于某区城市道路“白改黑”改造，以及大规模的城市建设，其规划区内等级控制点损毁严重，采用传统的测绘手段已不能满足城市规划建设的需要。

2 某区城市规划区坐标转换方法

通过CORS技术,我们能快速高效的获取待定点的厘米级精度WGS-84坐标和大地高，但是规划建设中常采用地方坐标系统和正常高，因此需要进行坐标转换和高程转换。某区采用重庆市独立坐标系统（东带）和1956年黄海高程系统。

Trimble Geomatics Office软件（TGO）提供了点校正及坐标系统转换工具，通过平面转换和高程转换，能将WGS-84坐标和大地高转换至地方坐标系统和高程系统。

（1）平面坐标系统转换模型采用四参数模型：

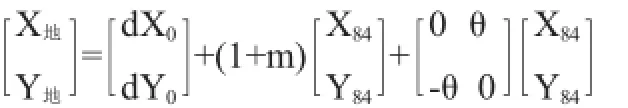
式中：dX0、dY0、m、θ分别为坐标平移量、缩放尺度和旋转参数。

平面转换模型原理简单，数值稳定可靠。但由于上式是一个线性变换公式，而Gauss投影变形是非线性的，因此平面转换模型只适合范围较小的工程使用。某区城市规划区面积约120km2，面积不大，可以采用平面转换模型进行坐标转换。

（2）GPS高程与正常高的转换

GPS接收机可以测定地面点的WGS-84中的大地高，也称为椭球高，一般用符号H表示。大地高是一个纯几何量，不具有物理意义。同一个点，在不同的基准下，具有不同的大地高。

而城市规划建设采用的是正常高，一般用符号Hγ表示。似大地水准面到椭球面的距离，称为高程异常，记为ζ。

即H=Hγ+ζ。

从前面的关系式可以看出，为了由GPS高程（大地高）确定出正常高，需要有高程异常数据，方可达到目的[1]。目前获取高程异常的方法有：a、等值线法,可以从全国高程异常图上通过内插法查求出点的ζ,但精度低，不能满足城市规划建设要求；b、地球模型法，本质上是一种数字化的等值线图，目前国际上较常采用的地球模型有OSU 91A、EGM 96等，不过这些模型均不适合于我国；c、高程拟合法，就是利用在范围不大的区域中，高程异常具有一定的相关性这一原理，采用数学方法求解高程异常。该方法简单易行，操作性强，在小范围内能够获取较高精度的高程异常；d、区域似大地水准面精化法，能够确定高精度、高分辨率似大地水准面，采用GPS技术结合区域内的地面重力资料、水准资料、高分辨率的地形数据以及最新的重力场模型，精确研究并确定区域似大地水准面，以求取高精度的高程异常，从根本上解决GPS技术无法直接提供正常高的问题。但是该方法技术难度大,需要的基础资料多,投资成本高，操作性不强。

高程拟合法可采用一次多项式模型和二次多项式模型。由于某区城市规划区面积小，本次研究拟采用一次多项式模型。

一次多项式模型为：

ζ=a0+a1dB+a2dL

或：ζ=a0+a1B+a2L

如果求出a0、a1、a2三个系数，就可以根据点的位置（B，L）求出点的高程异常，进而求出点的正常高。

3 某区城市规划区高程异常模型的建立

某区城市规划区高程异常模型计算拟采用Trimble Geomatics Office软件（TGO）提供了点校正及坐标系统转换工具。其计算结果形成*.dc文件形式[2]（如图1）。

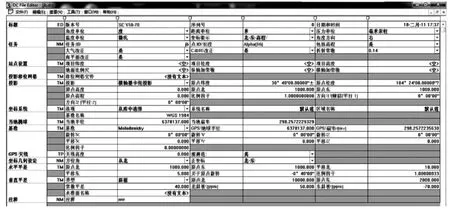
图1 ＊.dc文件形式

从图1中可以看出：Trimble Geomatics Office软件（TGO）采用四参数进行坐标转换，包括：平移北参数dxo、平移东参数dyo、关于原点旋转参数θ、比例因子参数m。采用一次多项式模型进行高程转换，包括：常数平差参数ao、北斜坡参数a1、东斜坡参数a2。

某区城市规划区面积约120km2，区域面积小，由于尤拉角很小(1"～2")，可以忽略尤拉角影响的差异，某区城市规划区高程异常模型建立采用四参数进行坐标转换，采用一次多项式模型进行高程转换。其规划区内有长江横穿东西，形成南北高、中部低的单面坡地势，由于采用一次多项式模型进行高程转换，因此根据地势条件，按照线性坡度方式将规划区分为A区域、B区域、C区域、D区域，分别建立高程异常模型。

各区域间相互重叠，重叠区域在不同区域高程异常模型中计算的高程值应满足一定的限差要求。分区范围见图2。

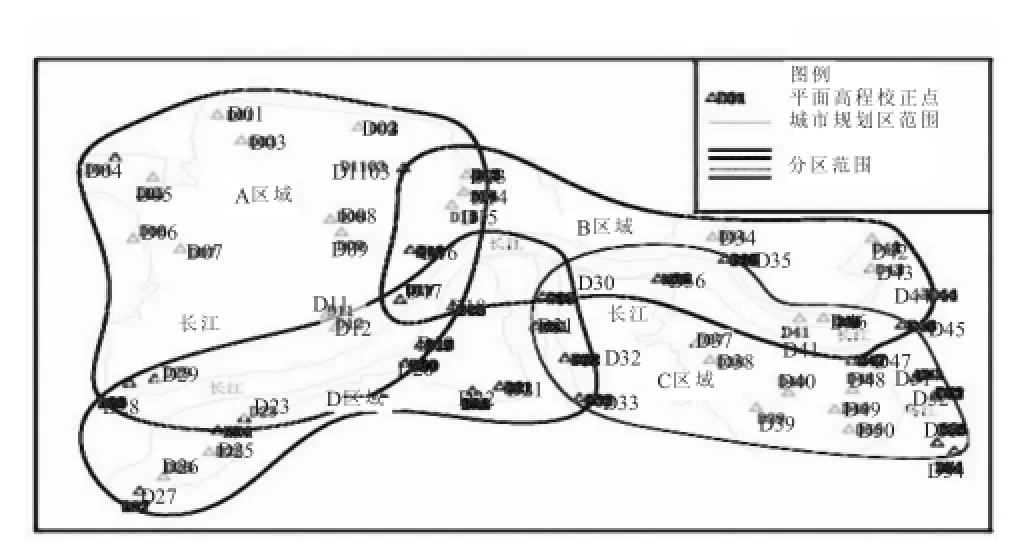
图2 某城市规划区高程异常模型建立分区示意图

采用Trimble Geomatics Office软件（TGO）提供了点校正及坐标系统转换工具，计算各分区的转换参数，各分区的转换精度见表1。

从表1可以看出：平面坐标转换的残差绝对值最大为19mm，根据《卫星定位城市测量技术规范》(CJJ/T73-2010)，平面坐标转换的残差绝对值不应超过20mm，满足规范要求；高程异常模型内符合中误差最大为29mm，按照CJJ/T73-2010规范图根等级的限差为30mm，也就是说某区城市规划区分区高程异常模型精度为图根精度。

为了检验分区模型精度的一致性，对重合区域校正点转换坐标进行比较，其较差比较表见表2。

表1 某区城市规划区分区坐标转换精度统计表

由误差传播定理知[3]，m重叠=则m重叠分量=m重叠/，取2倍中误差作为限差，由表1可计算重叠区域坐标分量及高程较差限差。由表2可知：各分区的坐标转换精度、高程异常模型精度是匹配的、可靠的。

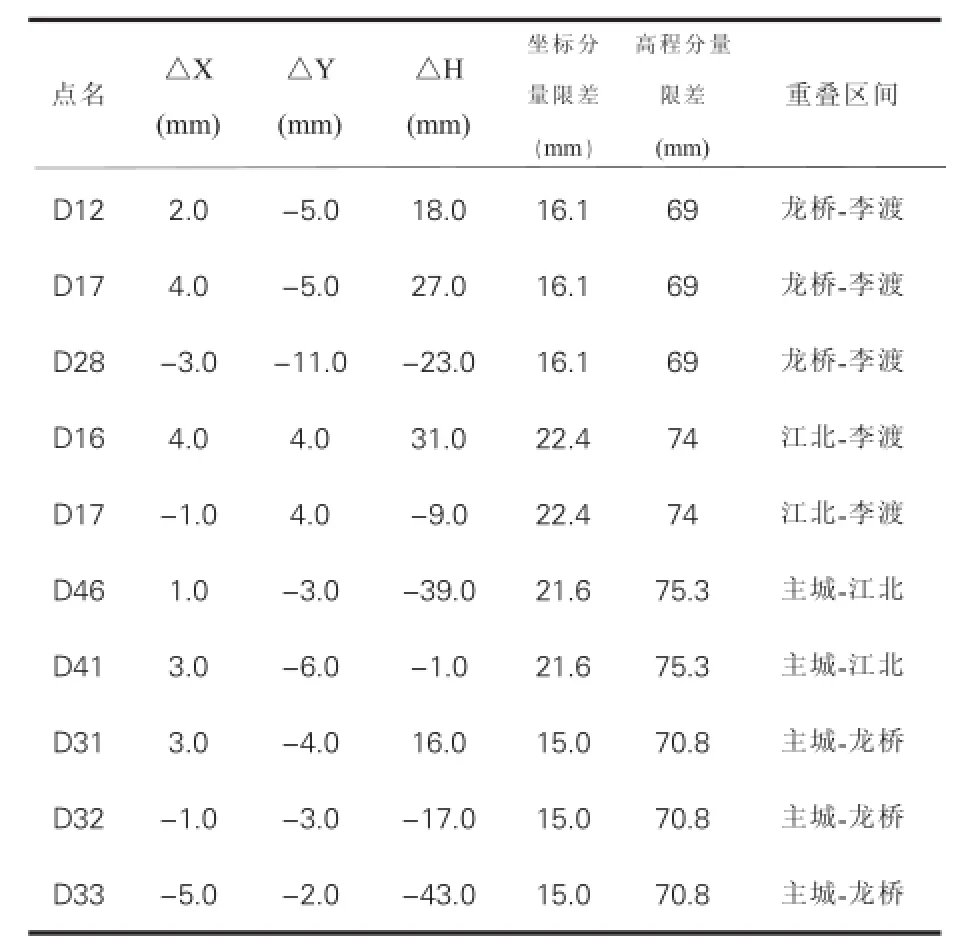
表2 重叠区域坐标比较表

上述分析仅检验了某区城市规划区平面坐标转换及高程异常模型内符合精度，下面通过外业测绘检校点来检验平面坐标转换及高程异常模型精度。检校点分布见图3。

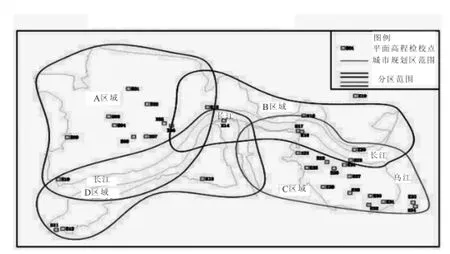
图3 某区城市规划区检校点分布示意图

通过网络RTK方法实测一级导线点的WGS-84坐标，采用Trimble Geomatics Office软件（TGO）提供了点校正及坐标系统转换工具，应用坐标转换参数和建立的高程异常模型，计算其重庆市独立坐标系统坐标及1956年黄海高程系统高程，并与其传统导线方法测绘的成果进行比较，精度统计表见表3。

从表3可以看出：某区城市规划区平面坐标转换及高程异常模型精度满足规范要求。

4 结论及建议

在中小城市规划区似大地水准面精化前，采用前述方法建立高程异常模型，应用网络RTK技术获取厘米高程成果是可行的。根据地形特征，分区域建立高程异常模型，能获得较高精度的平面高程转换精度，从而推动网络RTK技术的广泛应用，提高测绘在城市规划建设中的保障能力。

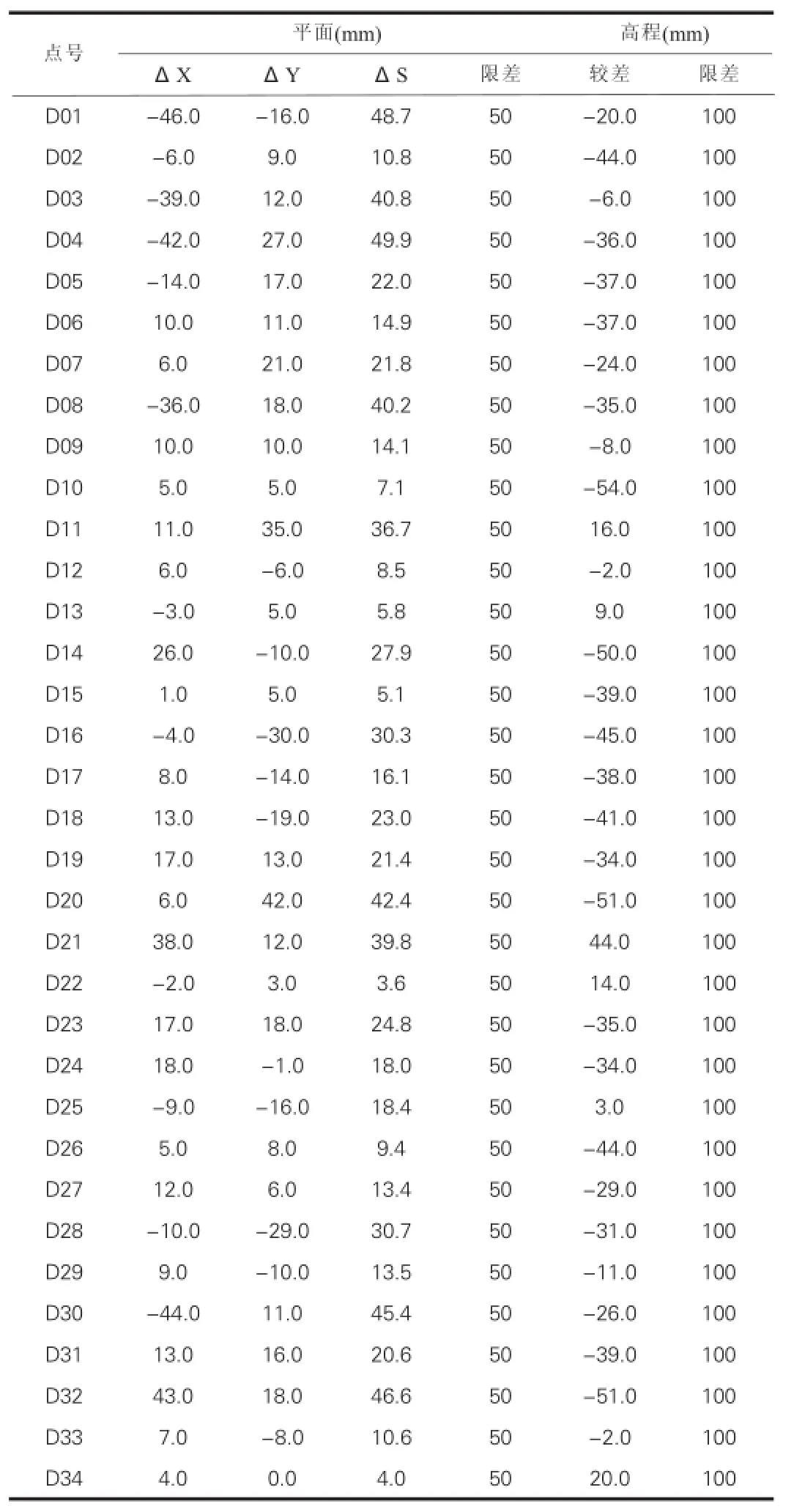
表3 某区城市规划区检校点精度统计表

[1]史经俭.GPS高程与正常高的转换[M].西安：西安电子科大出版社，2009.

[2]魏二虎，黄劲松.GPS测量操作与数据处理[M].武汉：武汉大学出版社，2004.

[3]於宗俦，鲁林成.测量平差基础.[M].武汉：武汉大学出版社，2003.

责任编辑：李红

Establishmentof Elevation Anomaly M odels in Smalland M edium-sized U rban Planning A reas

该文采用分区域按一次多项式方法建立城市规划区高程异常模型，解决中小城市WGS-84坐标至城市地方坐标高程系统的转换关系，推动了网络RTK技术的广泛应用，为城市规划建设提高了测绘保障能力。

CQCORS；坐标转换；高程异常模型

W ith the firstorder polynomialmethod,the authors establish elevation anomalymodels in differenturban planning areas by discretemethod, solving the transformation of the elevation system from WGS-84 coordinates to local coordinates in smallandmedium-sized cities,promoting thew ide application ofnetwork RTK technology and improving the surveying andmapping capacity for city planning and construction.

CQCORS;coordinate transformation;elevation anomalymodel

TU984.1

A

1671-9107（2012）06-0001-03

10.3969／j.issn.1671-9107.2012.06.001

2012-04-05

何德平（1972-），男，重庆人，本科，高级工程师，主要从事测绘工作与研究。