广义Γ－环上模的Morita结构及其应用

俞淑萍

（上海医疗器械高等专科学校基础部，上海 200093）

文献［1］引进广义Γ－环，本文研究这种环上模的Morita结构及其应用.该问题迄今尚未有人讨论过.本文中出现的广义Γ－环R均有α－单位元，∀α∈Γ.设M为R－右模，N为R－左模，Hom（M，N）表示M到N的模同态集，End（M）表示模M自同态集.本文中出现的不加定义的概念和符号见文献［1－2］.

1 广义Γ－环上模的Morita结构定义

根据结合环上模的Morita理论，可以定义广义Γ－环R上的模、α－自由投射模、投射生成模及α－张量积等概念.本文省略这些概念的定义过程，直接利用这些概念，并不加证明地给出广义Γ－环R上模的相应结果.

定理1 设P为R－模，则下列条件等价：

a.P为投射模；

b.任一短正合列0→M→N→P→0是点分裂的；

c.P为α－自由模的直和因子，即存在α－自由模F与R模P′使P⊕P′～F.

定理2 R－模P为投射模的充分必要条件是存在集

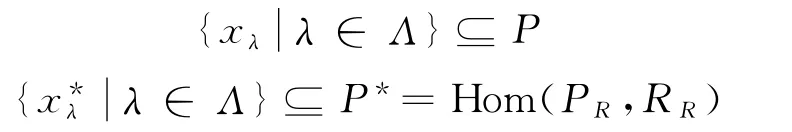
定理1和定理2可由广义Γ－环上模的运算特性，仿照文献［3－4］中结合环相应结果的证明即可证得.本文省略它们的证明.

定义1 设R′，R为广义Γ－环，M＝R′MR，M′＝RM′R′，若有R－R－同态τ和R′－R′－同态μ为

它们满足：任意x，y∈M，x′，y′∈M′，

即下面的两个同态映射图1（a）和图1（b）可交换，则称（R，R′，M，M′，τ，μ）为一个Morita结构.

图1 同态映射交换图Fig.1 Homomorphic figure

2 构造M

定理3 设M＝MR为广义Γ－环R上的（右）模，从M出发构造它的一个Morita结构，并称之为构造M.

证明 令M＊＝Hom（MR，RR），R′＝End（MR），分别规定以下情形：

情形1 ∀α∈Γ，1α∈C1（R），设r′1，r′2∈R′，β∈Γ，m∈M，规定

则对任意ν∈Γ，x∈R

显然r′1βr′2∈End（M），故r′1βr′2∈ End（MR）.易验证R′关于这个结构构成广义Γ－环.1′α为R′的α－的单位元，且1′α∈C（R′）.为区别于环End（MR），将这个广义 Γ－环 R′记为EndΓ（MR），即R′＝EndΓ（MR）.特别地，若仅对α－而言，即Γ＝｛α｝，就得到广义α－环

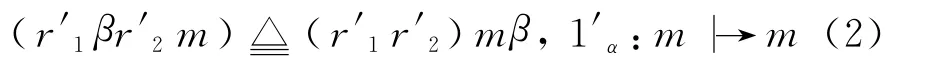
则R′也为广义Γ－环.

情形3 在情形1中，当r′∈R′，m∈M，β∈Γ时，规定

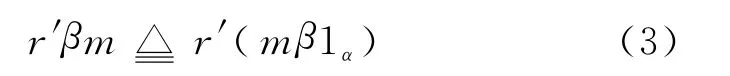
则MR为左R′－模，即M＝R′MR.

情形4 在情形2中，当r′∈R′，m∈M，β∈Γ时，规定

则MR为R′－模，即M＝R′MR.

情形5 在情形1中，当y＊∈M＊，r′∈R′，β∈Γ时，规定

则y＊βr′∈M＊且

情形6 在情形2中，当y＊∈M＊，r′∈R′，β∈Γ时，规定

对于情形1与情形2有下面的性质：

对于情形1，3，5，因1α∈C（R），1′α∈C（R′），故α－张量积就是张量积，令

其中，［m，y＊］：m1→mα（y＊，m1）＝mα（y＊m1），则τ为R－R－模同态，而μ为R′－R′－模同态.因

故［m，y＊］αm1＝mα（y＊m1）.同样，有x＊α［m，y］＝（x＊，m）αy＊.故由定义1可知，（R，R′，EndΓ（MR），M，M＊，τ，μ）为一个Morita结构.

对于情形2，4，6，可以取α－张量积作同态映射：

其中，［m，y＊］：m1→mα（y＊m1）.同样，（R，R′，M，M＊，τ，μ）为一个Morita结构.

综合上述情形，从M出发构造获得的Morita结构（R，R′，M，M＊，τ，μ），称为M的构造，仍记为M.

3 构造M的性质和应用

先证明构造M有以下性质.

定理4 在构造M中，若τ，μ是单射，则

a.MR，R′M，M′R，RM′均是投射模；

b.τ，μ是同构映射；

c.映射l：x′｜→l（x′），（l′（x′）：M→R；g｜→（x′，y））是RM′R′到RM′R′的双模同构映射；

d.C（R）与C（R′）同构.

证明 仿照文献［4］可证得结论a－d，本文省略证明.

现应用定理4，给出左、右Artin单广义Γ－环结构定理的另一个证明.

定理5 设R为广义Γ－环，则下列条件等价：

a.R为左、右Artin单的［1］；

b.R为单的且含极小右理想；

c.LαDnRα，其中，Lα为R的左α－算子环，Rα为R的右α－算子环，∀α∈Γ，Dn为除环D上的n阶方阵环.

证明 a⇒b.显然.

b⇒c.设R有极小右理想I，仿照文献［3］的引理1可得：存在e1∈R，ε∈Γ，使得f＝e1εR，e1ε1e1＝e1，且R有极小右理想的直和分解，R＝e1ε1R＋e2ε2R＋…＋enεnR.其中，eiεiei＝ei，eiεiR（i＝1，2，…，n）均为极小右理想.因此，作为右R－模，R为既约右R－模的直和，且I为R的直和因子，又显然I为有限生成的，而R为α－自由模，于是，由定理1可知，I为有限生成投射模，由定理5可知，τ（1）≠0，由τ为单的，可知τ（I）＝R，即I为投射生成模.按前文构造M，则有

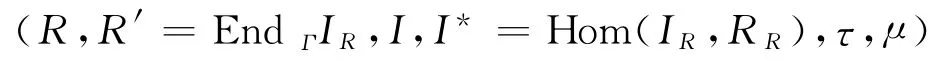
是一个Morita结构，现按情形1，3，5下的构造M与情形2，4，6下的构造M，分别证明定理5中的c成立.

若M是情形1，3，5下的构造，则由τ（I）＝R与τ，μ的定义可知，τ，μ均为满射，故定理1中各结论成立.因R有α－单位元1α，∀α∈Γ，由式（1），（3），（5）可知，R′α＝End IR′＝End IR′α，且R′α为除环.由定理4得I＊为有限生成右R′－模，且LαEnd，存在除环D与正数n.又显然有故有End

若M是情形2，4，6下的构造，则由式（2），（4），（6）可知，1αC（R）（∃α∈Γ），但由情形2，1′α∈C（R′），显然有意义，此时亦可证End＝End，从而式（5）成立.事实上，设显然，有；反之，设∈I＊，r′∈R′，φ（m＊αr′）＝（φm＊）αr′，对∀β∈φ，φ（m＊βr′）＝φ（m＊α1′αβr′）＝φ（m＊）α1′αβr′＝（φm＊）βr′，又显然所以于是，End

现给出一实例说明定理5的应用.

例1 取除环D上n阶方阵环R＝Dn，

μ如前文中定义，由定理3得（R，R′，M，M＊，τ，μ）为M的构造M，且满足定理5中的条件c.故由定理5可知，R＝Dn是一个左、右Artin单的广义Γ－环.

［1］ 高振林.广义Γ－环的交换条件［J］.曲阜师范大学学报，1987，13（3）：205－208.

［2］ Gao Z L.On Rees matrix representations of abundant semigroups untri adequate transuersals［J］.Commun Korean Math Soc，2009，24（4）：481－500.

［3］ Nobusawa.On a generalization of ring theory［J］.Osaka J Math，1964，23（1）：81－89.

［4］ Jacobson N.Basic AlgebraⅡ［M］.San Fancisco：W H Freeman and Company，1980.