利用延时预处理的DOA估计方法

司伟建，林晴晴

(哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001)

波达方向(direction of arrival，DOA)估计是阵列信号处理领域的一个重要研究方向，在雷达、声呐、通信及医学成像等领域有着广泛的应用前景.其中子空间类测向算法因其可同时对多个到达信号进行测向，测角精度也远高于的传统测角方法而成为研究热点.MUSIC算法［1］是其中一种经典的子空间类算法，该算法主要是利用噪声子空间与信号子空间的正交性进行DOA估计.由MUSIC算法的分辨力门限［2-3］可知，其分辨力与信噪比、快拍数等因素有关，而在实际测向系统中这些影响因素均受到条件限制［4］，因此也限制了MUSIC算法的分辨力.基于四阶累积量的波达方向估计方法［5-6］可以提高阵列的分辨力，但是四阶累积量协方差矩阵的构造以及新阵列流型的谱峰搜索过程非常复杂.文献［7］提出的算法提高了阵列的分辨力，但是需要先估计变换矩阵，计算变得复杂，且对变换矩阵的估计精度会影响DOA估计的精度.经典MUSIC算法利用零延迟相关函数计算接收数据协方差矩阵，隐藏在非零延迟相关函数中的信息没有得到充分利用.文献［8］利用高阶累积量算法将延迟相关函数应用于波达方向估计的预处理中，但基于高阶累积量测向算法的计算量却增大很多.刘剑等［9-10］利用延迟相关函数及其共轭信息提出了二阶预处理的SO-CAM算法，但是仅利用了部分相关信息.本文提出了一种利用延时预处理的DOA估计方法，引入变尺度混沌优化算法来简化空间谱函数的构造和谱峰搜索过程，在保证一定的测角精度的情况下减少算法的计算时间.

1 信号模型

假设有D个窄带不相关的信号从远场入射到空间M元阵列上，第i个信号的入射角度信息为(θi，φi)，噪声是均值为零、方差为σ2加性高斯白噪声.以原点为参考点，第m个(m=1，2，…，M)阵元的位置为(xm，ym)，其接收数据为

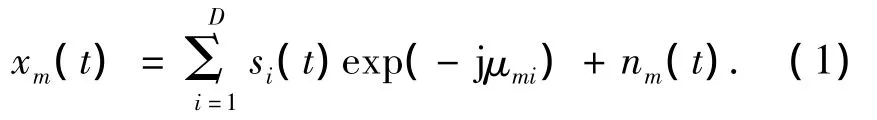
式(1)写成矩阵矢量形式:

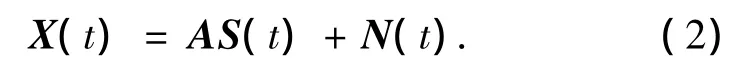
式中:X(t)为阵列的M×1维接收数据矢量，S(t)为空间信号的D×1维矢量，N(t)为阵列的M×1维噪声数据矢量，A=［a1a2…aD］为阵列的M×D维流型矩阵，且

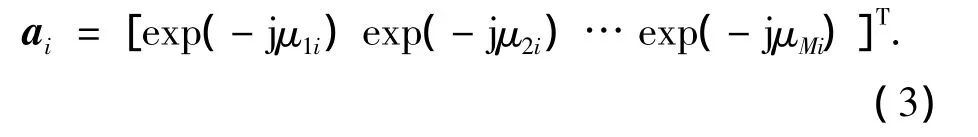
阵列输出的协方差矩阵为

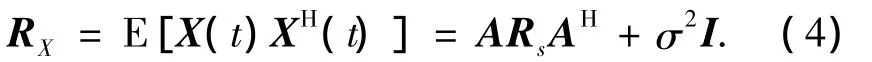
式中:Rs=E［S(t)SH(t)］为信号协方差矩阵，σ2I为噪声协方差矩阵.

对协方差矩阵进行特征分解有

式中:λi为特征值，对其进行由大到小排序:λ1≥…≥λD≥λD+1≥…≥λM;ΛS=diag(λ1，…，λD)是前D个大特征值构成的对角阵，US=［e1，…，eD］是由其对应的特征向量张成的信号子空间;ΛN= diag(λD+1，…，λM)是由后M－D个小特征值构成的对角阵，UN=［eD+1，…，eM］是由其对应的特征向量张成的噪声子空间.由

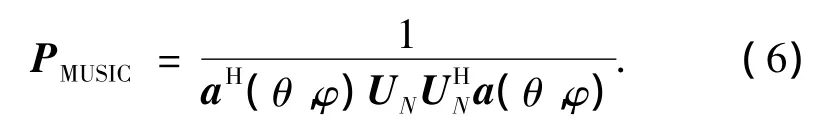
构造MUSIC算法的空间谱估计函数，通过搜索其极值点得到入射信号的波达方向.

2 利用延时预处理的DOA估计方法原理

MUSIC算法理论上有优良的分辨性能，但是在实际测向系统中，由于信噪比及快拍数都有限，限制了MUSIC算法的分辨率和测角精度.本文提出的基于阵元间接收数据的延时相关函数的DOA估计算法，充分利用了蕴含在接收数据的延时相关函数中的信号角度信息，可以有效提高阵列的分辨率和测角精度.

构造任意2个阵元(第m和第n个阵元，m，n= 1，2，…，M)接收数据的延时相关函数为

式中:Rsi(τ)=E［si(t)(t－τ)］为入射信号si(t)的自相关函数;Rnmnn(τ)=E［nm(t)(t－τ)］为噪声的互相关函数.

当存在一定的时延τ时，这里可以令时延τ远小于入射信号带宽的倒数，在时间τ内入射信号包络的变化可以忽略，而噪声不再具有相关性，此时信号和噪声存在一个可分离特性.在实际系统中，信号在时间上具有相关性，当接收机的带宽较宽时，噪声的功率谱近似为一条直线，在时间上可以认为噪声是不相关的，因此有

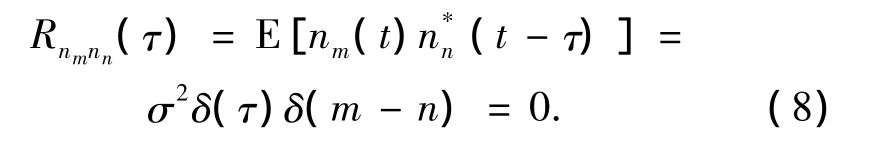
则式(7)可以写为

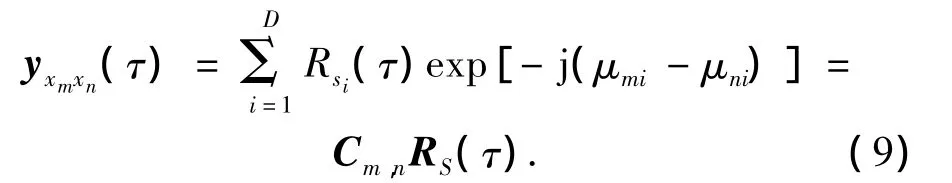
式中:RS(τ)=［Rs1(τ)Rs2(τ) … RsD(τ)］T，Cm，n=［exp{－j(μm1－μn1)} … exp{－j(μmD－μnD)}］.

可以将Cm，n写成2个矩阵相乘的形式，即

式中:Bn=diag(exp(jμn1)，exp(jμn2)，…，exp(jμnD))为对角阵，Am为阵列流型矩阵 A的第m行，且Am=［exp(－jum1)，exp(－jum2)，…，exp(－jumD)］.

由此可得阵元间的延时相关函数为

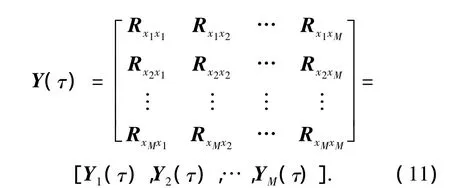
式中:Yk(τ)为Y(τ)的第k列(k=1，2，…，M)数据，结合式(10)可得

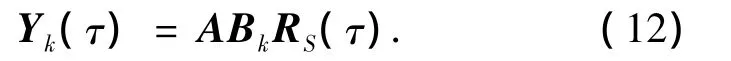
由延时相关函数构造新的协方差矩阵为

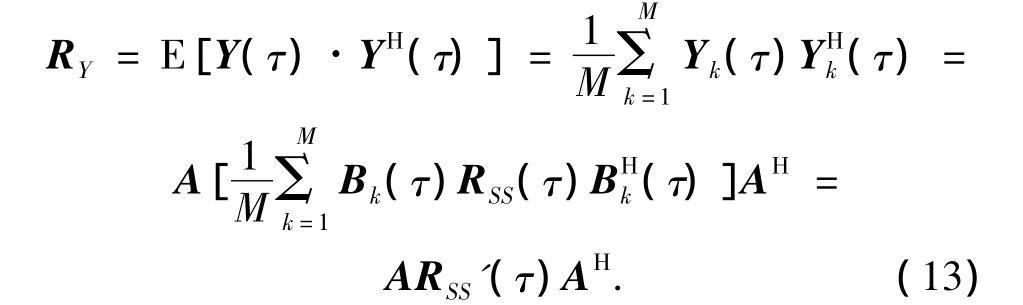
式中:RSS=E［RS(τ)R(τ)］为信号的协方差矩阵，为经过延时相关处理的信号的协方差矩阵.由上式看到新的协方差矩阵不受加性高斯白噪声的影响，即本算法可以有效地抑制噪声.

对比式(4)，经过延时相关处理得到的协方差矩阵保留了原协方差矩阵的流型矩阵，改变了信号的协方差矩阵，这对信号子空间与噪声子空间的构成没有影响，因此可以利用子空间类算法估计信号的到达角.

经过延时相关处理得到的协方差矩阵充分利用了所有阵元间的延时相关信息，增加了协方差矩阵的信息量，可以有效提高阵列的分辨率和测角精度.

实际接收数据是有限长的，因此得到的协方差矩阵为其估计值，即式(8)右侧不为零，但是其值为接近于零的一个很小的值，噪声项依然可以得到有效抑制.设一次估计所用的快拍数为N，则数据协方差矩阵的最大似然估计为

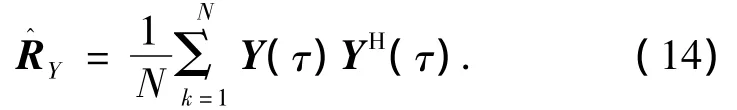
对式(14)进行特征分解，得到M个特征值并由大到小进行排序，取M－D个小特征值对应的特征向量构成噪声子空间U^N.

空间谱估计函数的构造和谱峰搜索过程是一个复杂且耗时的过程，影响着信号波达方向估计的测角精度和实时性.为了解决该问题，引入混沌优化的思想，用变尺度混沌优化算法［11-12］来简化空间谱函数的构造和谱峰搜索过程.具体过程如下:

采用Logistic映射产生混沌变量:

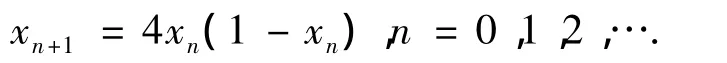
1)初始化.设置循环数L和N，以及搜索到较优值的次数K，令k=0.在［0，1］内随机选取i个(i= 1，2，…，D)微小差异的初始值xi，0，并令=xi，0，优化变量区间［ci，bi］，设置优化函数的初始值p*(x)为一个较小的数;

2)把xi，n分别映射到对应的定义域中:xi，n'= ci+xi，n(bi－ci)，将其代入到优化函数中并进行比较:若p(xi，n')＞p*(x)，则令p*(x)=p(xi，n')，;若k≥K，则转入步骤4)，否则进入步骤3).

这里的优化函数由式(6)来计算，即优化函数可以写为

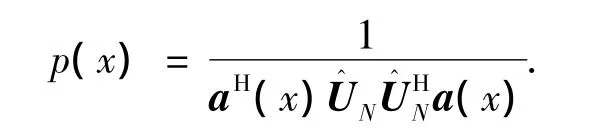
3)将xi，n代入Logistic式中得到:

5)令m=m+1.如果m＜L，则令ci=ci'，bi= bi'，并且返回步骤2)，否则进入步骤6);

6)满足搜索停止条件，从较小的p*(x)中得到最优参数值.

传统的谱峰搜索过程计算量很大，尤其对于二维DOA估计，需要在方位角和仰角范围内计算空间谱函数值，然后进行谱峰搜索，也就是将某一谱函数值与相邻的4个值不断的进行比较来找出谱峰值.并且需要设置合适的角度搜索步长，搜索步长的大小与计算时间成反比.步长设置较小可以保证高的测角精度和分辨率，但是计算时间会急剧增大;步长较大可以缩短计算时间，但是测向性能会下降.而本文方法是通过生成混沌变量，将混沌引入到谱估计函数中，生成一个混沌状态，最后利用变尺度混沌优化算法来进行谱估计函数的构造和谱峰搜索便可得到入射信号波达方向.

总结本文算法具体步骤如下:

1)由式(7)、(11)计算阵元接收数据之间的延时相关函数，得到新的阵列输出矩阵Y(τ).

4)用变尺度混沌优化算法进行谱峰搜索，得到入射信号的波达方向.

3 DOA估计算法性能仿真分析

通过仿真实验验证本文所提出算法的性能，并与MUSIC算法及SO-CAM算法进行比较，仿真过程中所采用的阵列形式为均匀分布在圆周上的5元阵，噪声为加性高斯白噪声.

3.1 分辨概率

对不同信噪比条件下的分辨概率进行仿真，快拍数取300，进行100次独立实验，统计仿真结果如图1;对不同快拍数条件下的分辨概率进行仿真，信噪比取13 dB，进行100次独立实验，统计仿真结果如图2.实验中分辨概率的定义为能够正确分辨出所有角度的次数与实验次数的比值.

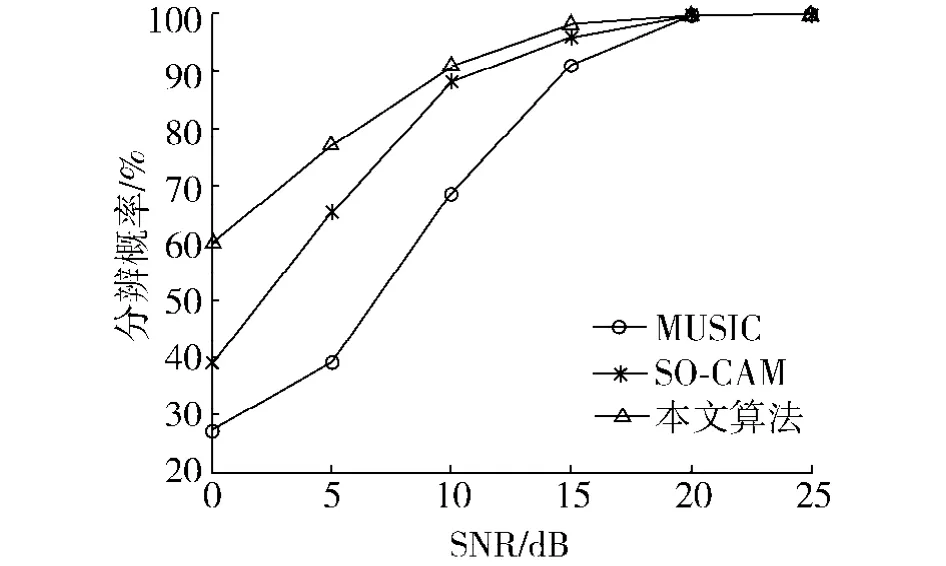
图1 分辨概率与信噪比的关系Fig.1 The relationship between resolution and SNR

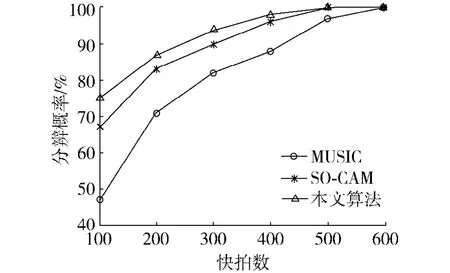
图2 分辨概率与快拍数的关系Fig.2 The relationship between resolution and snapshots

由图1、2可以看出，3种算法对2个信号的分辨概率均随着信噪比的增加而增大，随着快拍数的增多而增大，相同条件下本文提出算法的分辨概率相对SO-CAM算法和MUSIC算法均有一定的提高.本文算法充分利用了所有阵元接收数据的延时相关函数的信息，对信息的利用更加充分，因此提高了二维入射信号的分辨概率.

3.2 测角精度

对不同信噪比条件下的均方根误差进行统计，快拍数取300，进行100次Monte Carlo实验，统计仿真结果如图3;对不同快拍数条件下的均方根误差进行统计，信噪比取13dB，进行100次Monte Carlo实验，统计仿真结果如图4.第i(i=1，2，…，D)个入射角的均方误差定义为

由图3、4可以看到，3种算法估计结果的均方误差均随着信噪比的增加而减小，随着快拍数的增多而减小，同样的条件下本文算法的均方误差在3种算法中最小.本文算法相当于利用了所有阵元接收数据的延时相关函数的信息，对信息的利用更加充分，进而提高了测角精度.

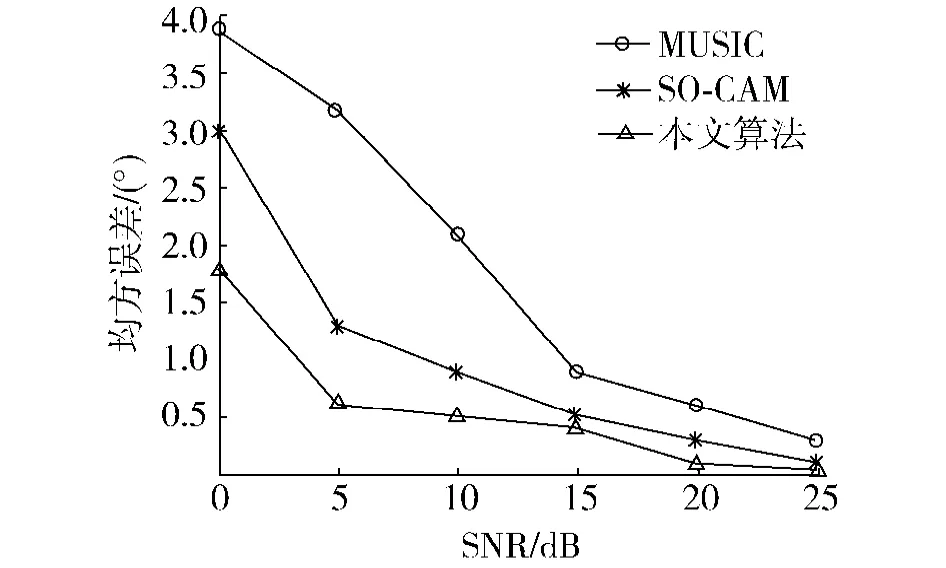
图3 均方误差与信噪比的关系Fig.3 The relationship between estimated variance and SNR

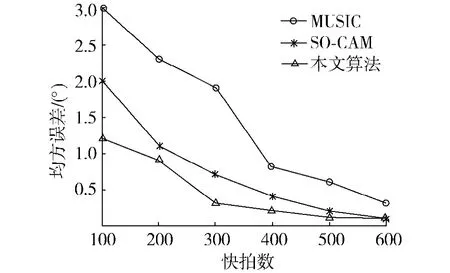
图4 均方误差与快拍数的关系Fig.4 The relationship between estimated variance and snapshots

3.3 计算时间

变尺度混沌优化算法进行谱峰搜索时共有3个常数:混沌搜索次数(内循环次数)、区间缩小次数(外循环次数)和混沌搜索找到较优值的次数.通过大量的仿真证明，三者的取值范围为100～1 000、 10～30、4～10时可以取得较好的效果.在仿真试验中，进行100次独立实验，对不同快拍数下的计算时间进行统计取平均，结果如表1.

表1 不同快拍数的计算时间Table 1 Computing time of different snapshots ms

引入变尺度混沌优化算法可以简化空间谱函数的构造和谱峰搜索过程，由实验结果可以看到，本文算法的计算时间明显减小.

4 结束语

本文提出了一种利用延时预处理的DOA估计方法，通过仿真实验表明:相比于传统MUSIC算法，本文算法具有较好的分辨率和较高的测角精度，这是因为本文算法利用了接收数据延时相关函数中蕴含的信号入射角度信息，对信息的利用更充分;在保证一定的测角精度的情况下，本文算法减小了计算时间，这是由于变尺度混沌优化算法简化了空间谱估计函数的构造和谱峰搜索过程，降低了运算复杂度.

［1］SCHMIDT R.Multiple emitter location and signal parameter estimation［J］.IEEE Transactions on Antennas and Propagation，1986，34(3):276-280.

［2］ZHOU C，HABER F，JAGGARD D L.A resolution measure for the MUSIC algorithm and its application to plane wave arrivals contaminated by coherent interference［J］.IEEE Transactions on Signal Processing，1991，39(2): 454-463.

［3］KAVEH M，BARABELL A.The statistical performance of the MUSIC and the minimum-norm algorithm in resolving plane waves in noise［J］.IEEE Transactions on Acoustics，Speech，and Signal Processing，1986，34(2):331-341.

［4］FERREOL A，LARZABAL P，VIBERG M.Statistical analysis of the MUSIC algorithm in the presence of modeling errors，taking into account the resolution probability［J］.IEEE Transactions on Signal Processing，2010，58(8): 4156-4166.

［5］刁鸣，陈超，杨丽丽.四阶累积量阵列扩展的传播算子测向方法［J］.哈尔滨工程大学学报，2010，31(5):652-656.

DIAO Ming，CHEN Chao，YANG Lili.Propagator method for direction of arrival estimation based on an array extension of the fourth-order cumulant［J］.Journal of Harbin Engineering University，2010，31(5):652-656.

［6］唐建红，司锡才，初萍.改进的基于四阶累积量的MUSIC算法［J］.系统工程与电子技术，2010，32(2):256-259.

TANG Jianhong，SI Xicai，CHU Ping.Improved MUSIC algorithm based on fourth-order cumulants［J］.Systems Engineering and Electronics，2010，32(2):256-259.

［7］KIM Y S，KIM Y S.Improved resolution capability via virtual expansion of array［J］.Electronics Letters，1999，35 (19):1596-1597.

［8］SHAN Z L，YUM T S P.A conjugate augmented approach to direction-of-arrival estimation［J］.IEEE Transactions on Signal Processing，2005，53(11):4104-4109.

［9］刘剑，于红旗，黄知涛，等.二阶共轭增强MUSIC算法［J］.信号处理，2008，24(3):411-413.

LIU Jian，YU Hongqi，HUANG Zhitao，et al.Second-order conjugate augmented MUSIC［J］.Signal Processing，2008，24(3):411-413.

［10］刘剑，于红旗，黄知涛，等.基于二阶预处理的共轭扩展MUSIC算法［J］.系统工程与电子技术，2008，30 (1):57-60.

LIU Jian，YU Hongqi，HUANG Zhitao，et al.Conjugate extended MUSIC algorithm based on second-order preprocessing［J］.Systems Engineering and Electronics，2008，30(1):57-60.

［11］邹恩，陈建国，李祥飞.一种改进的变尺度混沌优化算法及其仿真研究［J］.系统仿真学报，2006，18(9): 2426-2428.

ZOU En，CHEN Jianguo，LI Xiangfei.Improving mutative scale chaos optimization algorithm and simulation study［J］.Journal of System Simulation，2006，18(9):2426-2428.

［12］陈永倩，肖先赐.基于混沌寻优的DOA估计［J］.电子与信息学报，2005，27(3):388-391.

CHEN Yongqian，XIAO Xianci.Direction of arrival estimation based on chaotic optimization algorithm［J］.Journal of Electronics and Information Technology，2005，27 (3):388-391.