固支/对边固支对边自由矩形板模型

罗加智，刘土光，张涛

(华中科技大学船舶与海洋工程学院，湖北武汉430074)

复合材料优越的可设计性、高比强度、高比刚度，在工程结构中的应用日益广泛.由于同等刚度前提下，复合材料板一般比钢板厚度大得多，厚板结构在工程中更加常见，矩形板结构是主要的工程结构之一，有关矩形板的挠度问题是公认的难题.

文献［1］利用Galerk in方法分析了von-Karman型两邻边铰支两邻边夹紧正交各向异性矩形板;文献［2-3］分别基于Kirchhoff薄板理论，解决了三边固定一边自由矩形板和两对边固定两对边自由矩形板的弯曲;文献［4］用重三角级数分析对边简支对边自由的矩形薄板在均布荷载作用下的弯曲变形;文献［5］对矩形夹芯板振动作了几何非线性分析;文献［6］以3个位移分量及其一阶导数为状态变量，建立状态方程，考虑四边简支边界条件，得到了四边简支正交各向异性三维矩形板的精确解;文献［7-8］对各向同性轴对称复合圆板进行了三维线性分析.

经典薄板理论作了直法线假定，忽略了横向剪应力的影响.对于薄板小变形，它具有足够的精度，计算简便，但当厚度较厚或大变形时，横向剪切应力影响变得比较明显时，经典薄板理论不再适用.

一阶剪切理论由Mindlin［9］提出，假定板壳法线受力后仍为直线，但不再与中面垂直，引入了平均转角φx、φy，由此可得出横向剪切应力在厚度方向上均匀分布的结论，不能精确计算边界效应和层间应力.后来不少学者引入了剪切应力修正系数，改善一阶剪切理论的不足，但效果并不十分理想.

Reddy［10-11］在高阶剪切理论基础上，假定厚度方向不可压缩，得出了5参变量位移模型，在一定程度上减小了高阶剪切理论求解难度，相比一阶剪切理论，计算精度有了很大提高，但在计算横向剪切应力时误差比较大，不能满足工程设计需求.文献［12-13］均强调了横向剪切应力对厚板结构的影响，尤其对层合板结构的影响.

三维理论分析不做任何假定，可以精确反映面内和横向应力、应变，但很难得出精确的解析解.

本文提出了一种新的模型，该模型具有较少参变量，兼顾了应变在厚度方向的变化，保留了横向应力，并以均布横向载荷，四边固支及对边固支对边自由边界条件为例进行了探讨.

1 正交异性矩形板的边界条件

均布横向载荷下正交异性矩形板几何尺寸及坐标系见图1.

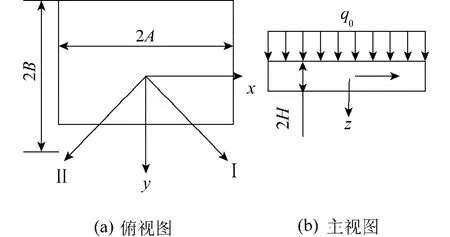
图1 矩形板坐标系统及形状Fig.1 Geometry of a rectangular plate

为简化及更具有一般性，设定短边为宽度2B，长边为长度2A，以半宽B为尺度，建立新的无量纲体系，即

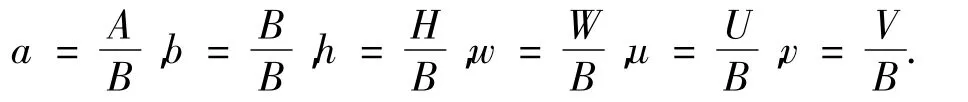
式中:W、U、V分别为z向挠度和x向、y向位移.

正交异性复合材料几何方程为

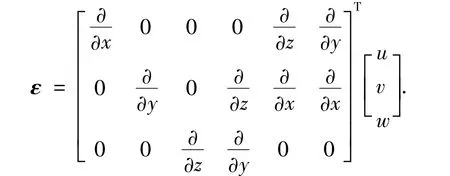
物理方程为

上、下自由表面有:z=±h，τyz=0，τxz=0.

边界条件如下:

1)四边固支边界CCCC:

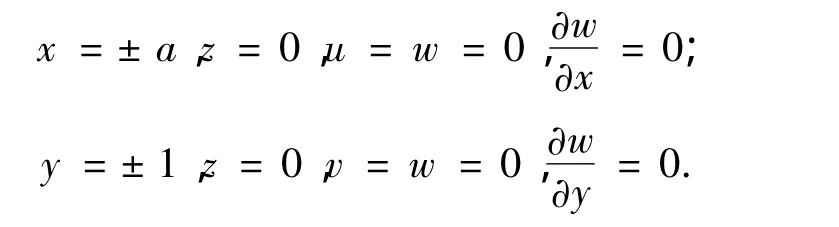
2)对边固支、对边自由边界CFCF:

本文假设x=±a边为固支，则边界条件为x= ±a，z=0时为自由边，位移在y向变化小，τyz为小量，忽略周边自由边界条件的影响，即:不考虑y=±1，z=0时，τyz=0.

2 位移数学模型

本文在分析时，假设:挠度与板厚相比为小量，挠曲面的斜率很小，忽略不计;弯曲后的中面保持无应变.设位移函数为

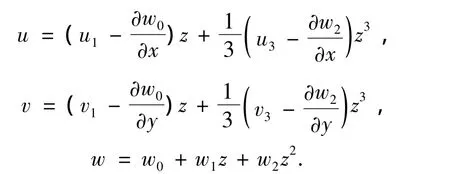
其中，ui、vi、wi为(x，y)的函数，则

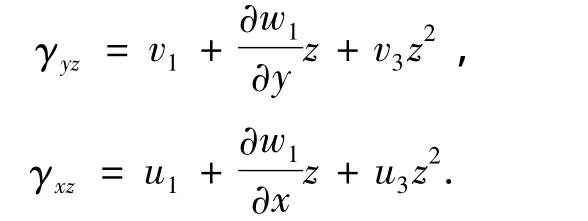
当z=±h时，γxz=γyz=0，可以得出:

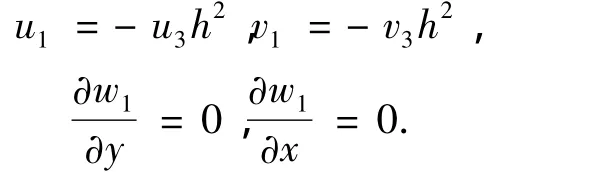
于是w1=c0，从而:

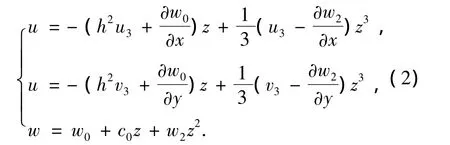
则横向剪应变为

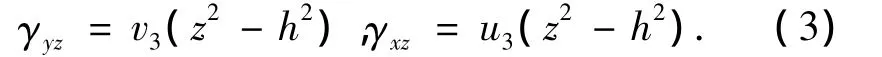
2.1 CCCC下的待定函数

具有四边固支边界的矩形板，在均布载荷下，当复合材料铺设角为零时，挠度具有双向对称性，面内位移具有垂向反对称性和切向对称性(垂向是指与位移垂直的方向，切向为与位移平行的方向，下文中如无特殊说明，定义相同)，同时，要满足挠度对面内坐标偏导在中面边界为零的条件，设定w0是 (a2－x2)2(1－y2)2的函数，w2是(1，x2，y2)的函数，令

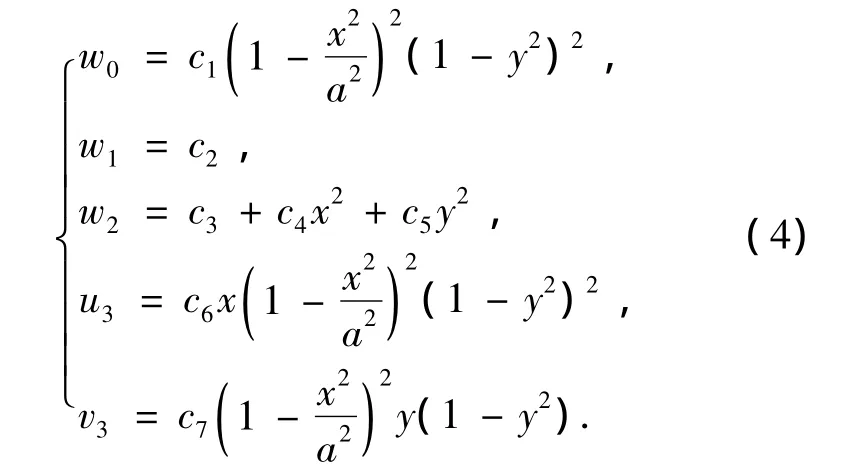
由式(4)可知，式(2)显然完全满足了四边固支边界条件，其中ci全部为待定系数.将式(4)代入式(3)，然后将结果代入式(1)，可求出横向剪应力，上下表面剪应力边界条件得到了满足，但周边剪力边界条件不满足.为满足剪力边界条件，可将式(4)中的u3、v3改为

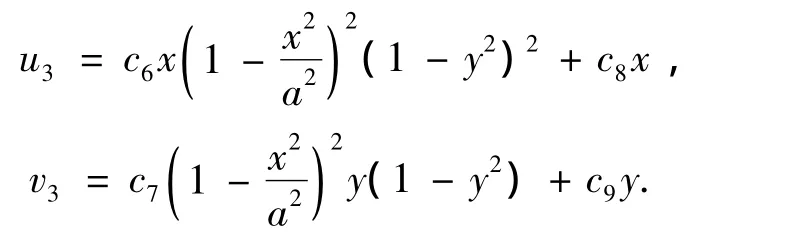
式中:c9=(3q/4h3－e55c8)/e44，其他ci为待定系数.

2.2 CFCF下的待定函数

具有对边固支、对边简支边界的矩形板，当固支边为x=±a，自由边为y=±1时，在均布载荷下，当复合材料铺设角为零时，挠度具有双向对称性，面内位移具有垂向反对称性和切向对称性，同时，要满足挠度在中面固支边为零，在自由边不为零，对面内坐标x的偏导在中面边界x=±a为零的条件，设定w0是((a2－x2)2，y2)的函数，w2是(1，x2，y2)的函数，令

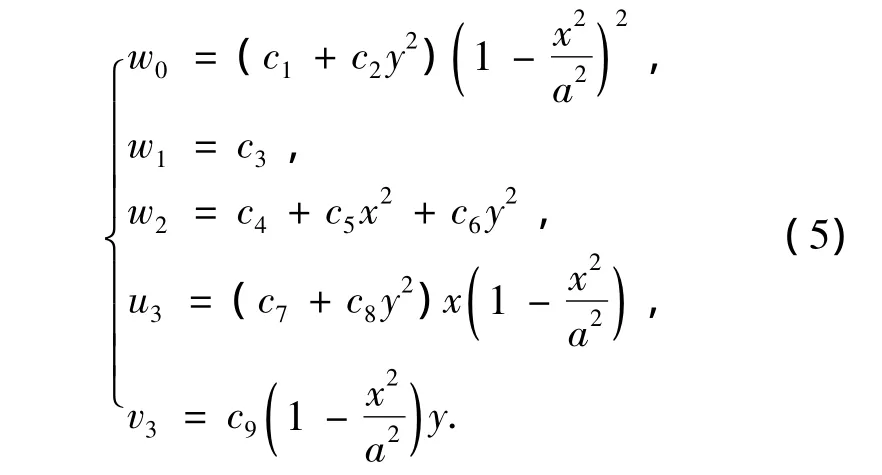
将式(5)代入式(2)，位移函数显然完全满足了固支边为x=±a，自由边为y=±1时的边界条件.当固支边为x=±1，自由边为y=±a时，只需要将x和y对调即可.将式(5)代入式(3)，然后将结果代入式(1)，可求出横向剪应力，但剪力边界条件不满足(ci全部为待定系数).为满足剪力边界条件，可将式(5)中的u3改为

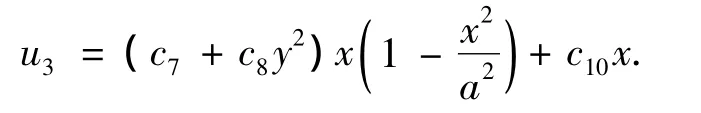
式中:c10=3q0/4h3e55，其他ci为待定系数.

3 计算示例

将本文提出的方法与有限元Ansys作了计算对比，各向同性材料与已有的经典理论公式［13］进行了对比.Ansys计算时选用了各向异性单元Solid64，单元尺寸0.04b，单元形状为六面体单元.由于材料性能、几何尺寸、载荷关于x，y轴对称，取1/4几何模型进行分析，在x=0面和y=0面施加对称约束.材料采用了文献［6］的正交异性材料和各向同性材料.正交异性材料(Ⅰ)材料常数为:E11=10E22= 10E33，G12=G13=0.6E33，G23=0.5E33，μ12=μ13= μ23=0.25;各向同性材料(Ⅱ)材料常数为:E= 100GPa，μ=0.3.

对于各向同性材料方板，文献［14］给出了四边固支边界条件下方板承受均布载荷时，发生在板中央的最大挠度计算式;文献［3］给出了对边固支、对边自由CFCF边界条件下方板承受均布载荷时，发生在板中央和自由边中心的最大挠度计算式.将上式无量纲化，并将抗弯刚度代入得:

1)四边固支边界条件CCCC:

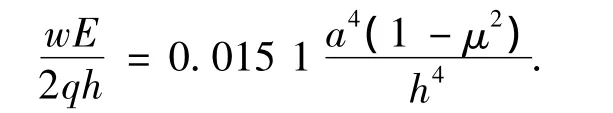
2)对边固支、对边自由CFCF:

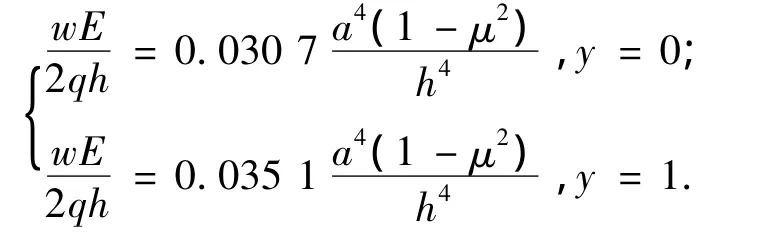
图2、3为采用正交异性材料Ⅰ，a=2，h=0.2，矩形板上表面挠度与Ansys的比较图.

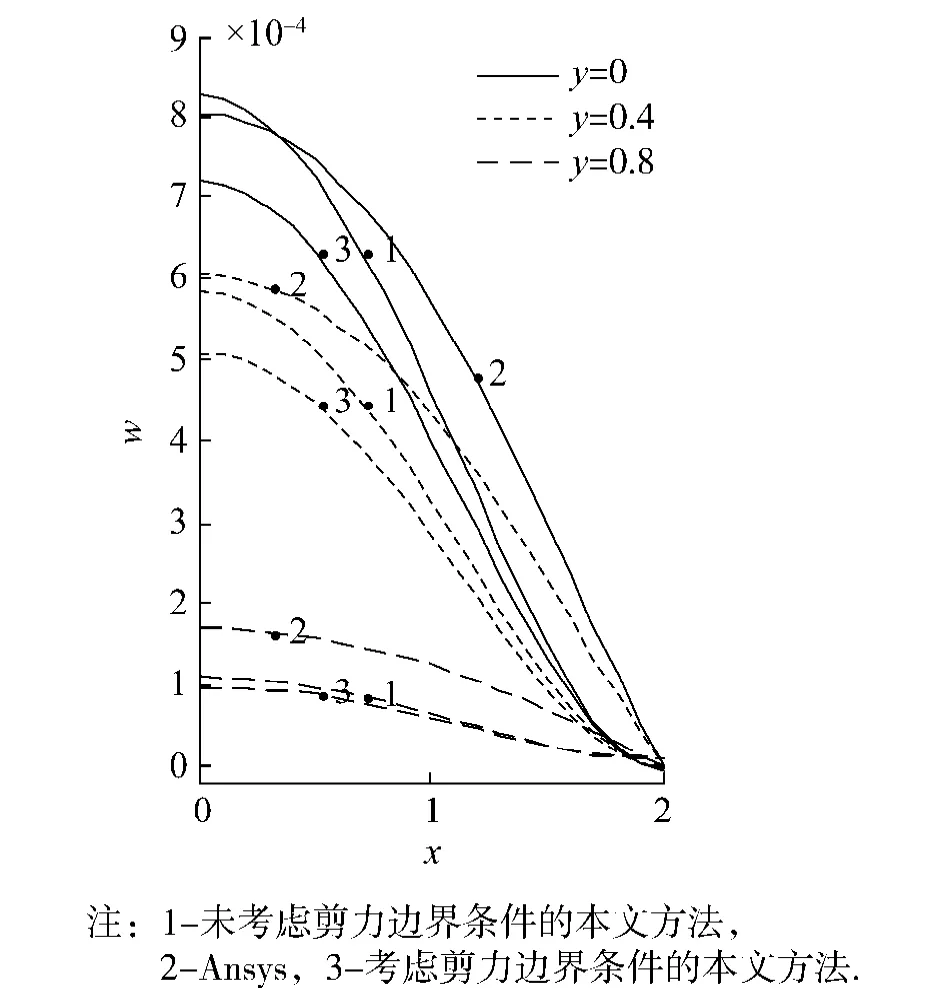
图2 CCCC条件下，矩形板上表面挠度分布Fig.2 Distribution of surface deflection of rectangular plate with CCCC

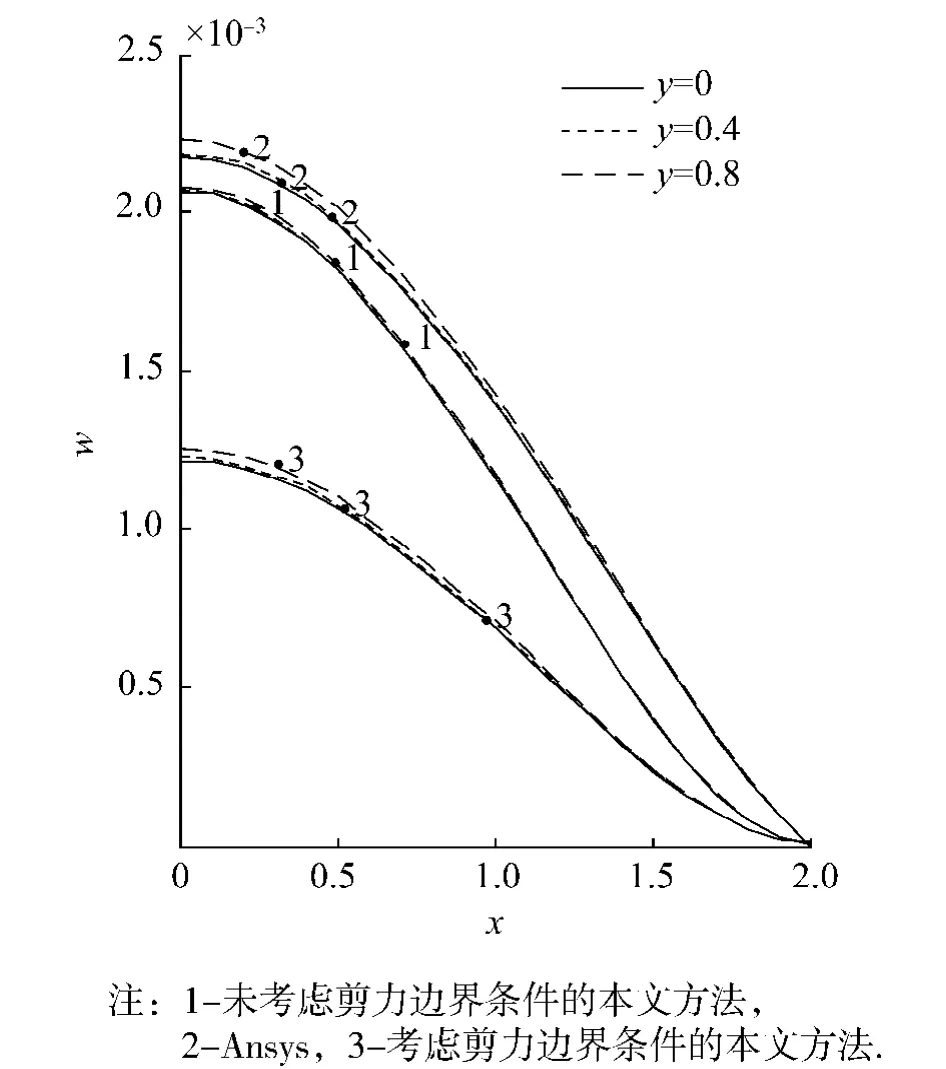
图3 CFCF条件下，矩形板上表面挠度纵向分布Fig.3 Distribution of surface deflection of rectangular plate with CFCF

图2、3表明以下规律:

1)没有考虑剪力边界条件时，与Ansys挠度计算值十分接近，二者计算出的上表面最大挠度的相对误差在四边固支边界条件下不超过3%;在对边固支、对边自由边界条件下相对误差不超过8%.

2)在固支边界上，所得曲线的斜率接近于零，而Ansys挠度曲线有较大的斜率.这一问题与有限元形函数设定有关，其影响有待于进一步研究.

3)考虑与不考虑剪力边界条件，在四边固支边界条件下及对边固支对边自由边界条件下结果明显不同.二者计算出的上表面最大挠度的相对误差在四边固支边界条件下，大于10%;在对边固支、对边自由边界条件下相对误差大于20%.

表1、2中的本文方法没有考虑剪力边界条件，对由正交异性材料构成的矩形板，采用不同的厚跨比、不同的长宽比，与Ansys进行了计算对比.

表1显示了在厚跨比变化时，方板具有的以下规律:1)在四边固支边界条件下，最大挠度计算值略大于Ansys计算值，相对误差不超过5%，且随厚跨比的增加，相对误差减小.2)在对边固支、对边自由的边界条件下，最大挠度计算值小于Ansys计算值，相差不超过8%，随厚跨比的增加，相对误差变化不大.

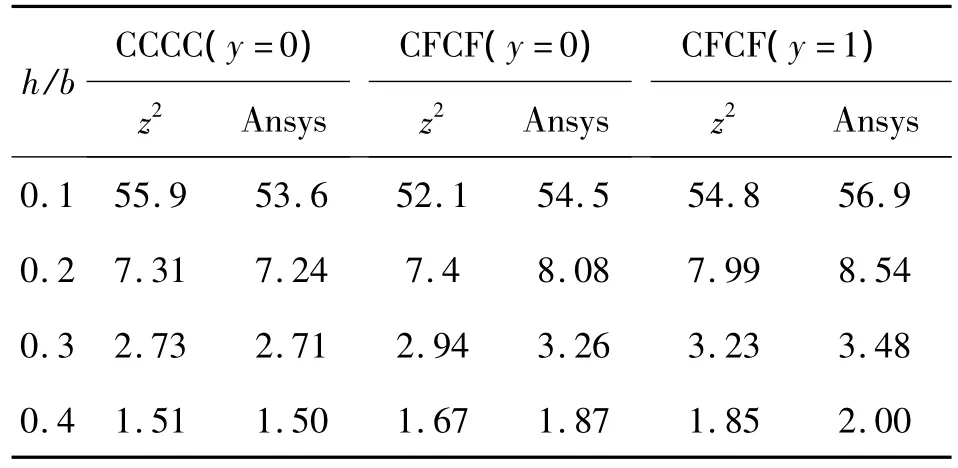
表1 材料Ⅰ在a=1，x=0，z=－h时的wE33/2qhTable 1 wE33/2qh of materialⅠwhile a=1，x=0，z=－h

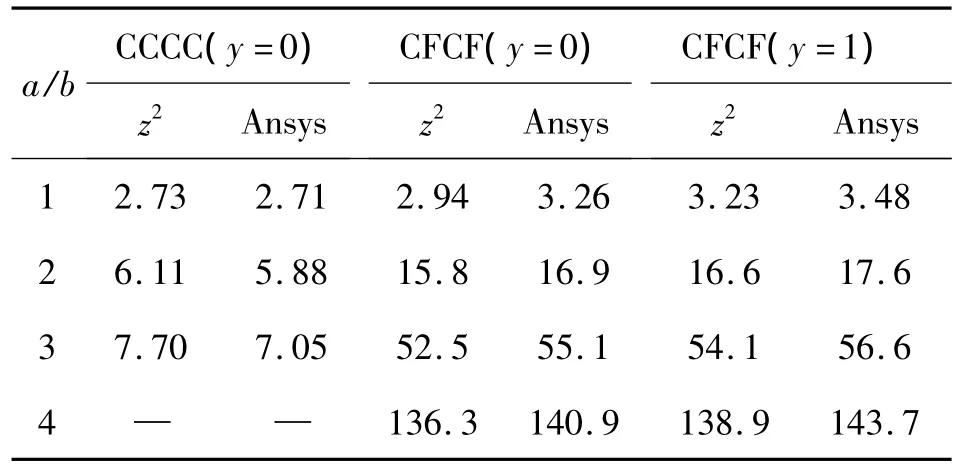
表2 材料Ⅰ在x=0，z=－h=－0.3时的wE33/2qhTable 2 wE33/2qh of materialⅠwhile z=－h=－0.3

表2显示矩形板在长宽比变化时，具有以下规律:1)在四边固支边界条件下，挠度最大值发生在中心，略大于Ansys计算值，当长宽比不大于2时，二者相对误差不超过5%，当长宽比不大于3时，二者相对误差不超过10%.2)在对边固支、对边自由的边界条件下，挠度最大值发生在自由边上，小于Ansys计算值，当长宽比大于2时，二者相对误差不超过5%，当长宽比小于2时，二者相对误差不超过8%.

表3、4中没有考虑剪力边界条件，对由各向同性材料构成的矩形板，在不同边界条件下，与Ansys及经典薄板理论进行了计算对比.计算采用了不同的厚跨比、不同的长宽比.表4中引用了文献［6］给出的对各向同性材料矩形板计算结果.

表3显示了方板，厚跨比变化时，具有的以下规律:1)在四边固支边界条件下，对于各向同性材料方板，不同的厚跨比，最大挠度略大于Ansys计算值，相对误差不超过5%，且随厚跨比的增加，相对误差减小;当跨厚比为0.05时，与经典理论值间的相对误差小于0.5%，Ansys与经典理论值间的相对误差为3.6%.2)在对边固支、对边自由的边界条件下对于各向同性材料方板，不同的厚跨比，最大挠度小于Ansys计算值，相对误差不超过6%，随厚跨比的增加，相对误差变化不大;当跨厚比为0.05时，与经典理论值间的租对误差小于0.5%，Ansys与经典理论值间的相对误差为1.6%;当跨厚比为0.1时，与经典理论值间的相对误差小于9.6%，Ansys与经典理论值间的误差为11.7%.3)当为薄板时，比Ansys更接近与经典理论值.

表4显示各向同性矩形板在长宽比变化时所具有的规律:1)在四边固支边界条件下，挠度最大值发生在中心，最大挠度略大于Ansys计算值，当长宽比不大于2时，二者相对误差不超过5%，当长宽比小于3时，二者相对误差不超过10%.2)在对边固支、对边自由的边界条件下，挠度最大值发生在自由边上，不同的长宽比，最大挠度略小于Ansys计算值，二者相对误差不超过5%.值得一提的是，当面内应力用本文方法求出后，横向应力可通过三维平衡方程精确求出，限于篇幅，本文未给出该示例.

表3 材料Ⅱ在a=1，x=0，z=－h时的wE33/2qhTable 3 wE33/2qh of materialⅡwhile a=1，x=0，z=－h

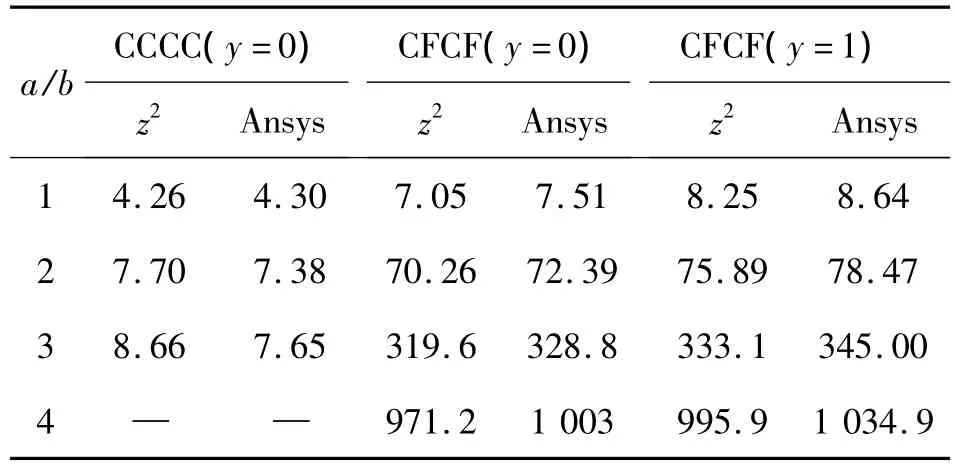
表4 材料Ⅱ在x=0，z=－h=－0.3时的wE33/2qhTable 4 wE33/2qh of materialⅡwhile x=0，z=－h=－0.3

4 结论

本文通过对一阶剪切理论、高阶剪切理论的分析，以均布横向载荷，各类边界条件为例，探讨了适用于各类板厚正交异性矩形板的新的数学模型，并通过计算示例得如下结论:

1)通过与Ansys和经典理论计算结果比较可知，不同边界条件下矩形板在均布横向载荷作用下，挠度变化规律与Ansys基本一致，表明提出的复合材料矩形厚板受均布荷重的位移函数是合理可行的.

2)当不计及剪力的边界条件时与Ansys计算结果接近，当计及剪力边界条件时，位移值略小于Ansys的位移值.

3)当面内应力用本文方法求出后，横向应力可通过三维平衡方程精确求出.

［1］杨加明，孙良新，吴丽娟.两邻边铰支两邻边夹紧正交各向异性矩形板的中等大挠度［J］.复合材料学报，2001，18(4):103-107.

YANG Jiaming，SUN Liangxin，WU Lijuan.Moderate large deflection of orthotropic rectangular plates with two adjcent edges simply supported and the other two adjcent edges clamped［J］.Acta Materiae Compositae Sinica，2001，18 (4):103-107.

［2］岳建勇，曲庆璋.三边固定一边自由矩形板的精确解［J］.青岛建筑工程学院学报，1999，20(1):16-21.

YUE Jianyong，QU Qingzhang.The precise solution of rectangular plate with three edges built in and the fourth edge free［J］.J of Qingdao Institute of Architecture and Engineering，1999，20(1):16-21.

［3］岳建勇，曲庆璋.两对边固定两对边自由矩形板的精确解［J］.青岛建筑工程学院学报，2000，21(2):12-31.

YUE Jianyong，QU Qingzhang.Exact solution of rectangular thin plates with two opposite edges clamped and the other two edges free［J］.J of Qingdao Institute of Architecture and Engineering，2000，21(2):12-31.

［4］王效民，刘新东，汤翔.重三角级数解一对边简支一对边自由的矩形板［J］.山西建筑，2007，33(29):12-13.

WANG Xiaomin，LIU Xindong，TANG Xiang.Rectangular board of heavy triangle grade solution with one side simple and another free［J］.Shanxi Architecture，2007，33(29): 12-13.

［5］LI Y Q，LI F，HE Y L.Geometrically nonlinear forced vibrations of the symmetric rectangular honeycomb sandwich panels with completed clamped supported boundaries［J］.Composite Structures，2011，93:360-368.

［6］杨正光，仲政，戴瑛，等.四边简支厚板的三维弹性分析［J］.同济大学学报，2003，31(12):1431-1433.

YANG Zhengguang，ZHONG Zheng，DAI Ying，et al. Three dimensional elasticity analysis of simple supported orthotropic rectangular thick plates［J］.J of Tongji University，2003，31(12):1431-1433.

［7］罗加智，刘土光，张涛，等.各向同性轴对称复合圆板的三维线性分析［J］.哈尔滨工程大学学报，2004，25 (3):274-279.

LUO Jiazhi，LIU Tuguang，ZHANG Tao，et al.Linear three-dimension analysis for sandwich axially symmetrical circular plates［J］.J of Harbin Engineering University，2004，25(3):274-279.

［8］LOU J Z，LIU T G，ZHANG T.Three-dimensional linear analysis for composite axially symmetrical circular plates［J］.Int J of Solids and Struct，2004，41(14):3689-3706.

［9］MINDLIN R D.Influence of rotatory inertia and shear on flexural motions of isotropic，elastic plates［J］.J Appl Mech ASME，1951，18:31-38.

［10］REDDY J N.A simple higher-order theory for laminated composite plates［J］.J Appl Mech ASME，1984，51: 745-752.

［11］REDDY J N.A refined nonlinear theory of plates with transverse shear deformation［J］.Int J Solids Struct，1987，20:881-896.

［12］ZHANG Y X，YANG C H.Recent developments in finite element analysis for laminated composite plates［J］.Composite Str，2009，88:147-157.

［13］FIEDLER L，LACARBONARA W，VESTRONI F.A generalized higher-order theory for buckling of thick multi-layered composite plates with normal and transverse shear strains［J］.Composite Str，2010，92:3011-3019.

［14］UGURAL A C.板壳应力［M］.范钦珊，译.北京:中国建筑工业出版社，1986:46-47.