变形晶体X射线分光性能的数值模拟
2012-03-22徐中民王纳秀
王 丽 徐中民 王纳秀
1 (中国科学院上海应用物理研究所 上海 201800)
2 (中国科学院研究生院 北京 100049)
上海同步辐射光源的辐射功率高,其高热负载会降低光束线分光元件性能,甚至失效。晶体单色器是同步辐射装置光束线关键器件,对X射线起单色化作用,其分光效果决定X射线的能量分辨率。X射线经双晶单色器第一块晶体后强度降低[1],对第二块晶体的热效应影响可忽略,因此,本文研究晶体单色器第一块晶体的Darwin宽度变化。
晶体单色器从连续的同步辐射光谱中分离出单一波长的 X射线,须满足晶体 Bragg衍射方程mλ=2dsinθB。由于晶体承受高热负载、冷却水压力和机械安装变形等因素影响,导致其晶格参数或晶面方向发生改变,造成晶体 Darwin宽度及 Bragg角θB选择的单色X射线能量带宽发生展宽,从而降低晶体的分光性能。将上式微分,得晶体 Bragg反射的本征能量分辨率为Δλ/λ=ΔE/E=ΔθBcotθB,式中的ΔθB是晶体Bragg反射角宽度(Darwin宽度)。本文通过有限元软件计算同步辐射晶体单色器晶体变形位移,确定晶体倒格矢的改变量,按变形晶体光学理论预测变形晶体的Darwin宽度,建立一套预测直接水冷却晶体单色器分光性能的方法,并应用于同步辐射光束线晶体单色器的设计和加工。通常采用面形误差法预测双晶单色器分光性能,即计算晶面斜率误差的RMS值。面形误差法较成熟,但其预测结果不能很好反映实际变形晶体的 Darwin宽度的展宽。文中采用倒格矢法和面形误差法数值模拟方法分别对简单机械压弯晶体、弧矢聚焦月牙槽直接水冷却晶体变形晶体分光性能进行表征,并结合试验结果比较了两种方法的优劣。
1 数值模拟方法
1.1 倒格矢法
采用文献[2]的ANSYS有限元软件计算变形晶体倒格矢的方法:

其中,I是单位矩阵, (hx', hy', hz')是变形后晶体倒格矢的三个分量,(hx, hy, hz)是晶体未变形时倒格矢的三个分量,U是位移量相对于位置的偏导数的矩阵。它是一个平均值,需求出节点在其被共有的每个单元中U值,再进行平均。而ANSYS软件中不能提供直接的计算,因此对于U值需进行下列计算。
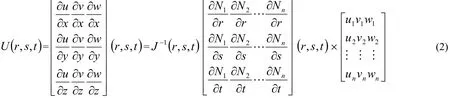
雅可比行列式
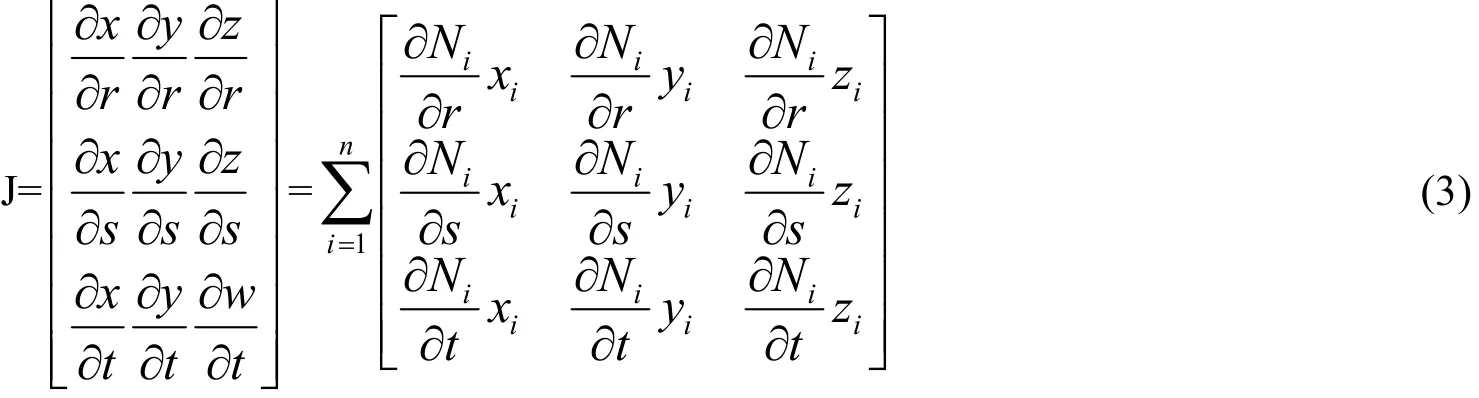
式中,(r, s, t)为单元坐标系中节点的位置坐标,(x, y, z)为全局坐标系中节点的位置坐标。Nn是单元的第n个节点的形函数,(u, v, w)是全局坐标系中节点的位移量。
U的计算分为两步:
(1) 计算每个单元积分点的位移量相对于位置的偏微分矩阵。ANSYS软件可给出每个单元的节点全局坐标下的位置和位移量。形函数 Nn可在ANSYS手册中查到,不同单元对应不同的形函数。将节点的位置坐标、位移量、形函数代入式(2)可计算全局坐标下每个积分点(rint, sint, tint)的位移量相对于位置的偏微分矩阵U(rint, sint, tint)。
(2) 计算每个节点的位移量相对于位置的偏微分矩阵U(ri, si, ti)。这里只用8个角积分点(rint, sint, tint)=(±A, ±A, ±A),不同类型单元的A值各不不同,对本文计算中采用的SOLID95单元,A=0.758686910639328[3]。每个节点的U(ri, si, ti)由式(4)给出:
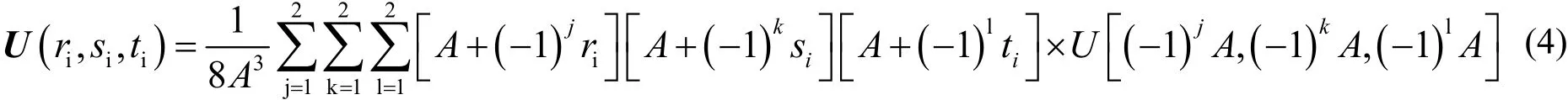
由于每个节点被几个单元共有,同一节点在不同单元中的U(ri, si, ti)通常不等,因此,计算每个节点的U(ri, si, ti)时需将其在每个单元的值进行平均(即Uavg),然后代入式(1),算出每个节点处的倒格矢。
本文用实际晶体在衍射光束时的Bragg角与理想Bragg角的差值表征晶体Darwin宽度展宽,即用Bragg角的变化表征变形后晶体子午方向的Darwin宽度展宽。变形后晶体子午方向的Darwin宽度展宽的计算方法如下:先由已知的计算,为在入射波矢与未变形的倒格矢所确定的面上的投影。晶体的Darwin宽度展宽Δω为:

式中,θ1为与的夹角,即晶体变形后的入射角补角,θ2为与的夹角,即完整晶体的入射角补角(图1)。本文计算兴趣区内每个节点的入射角即Bragg角的变量(ΔθB)。
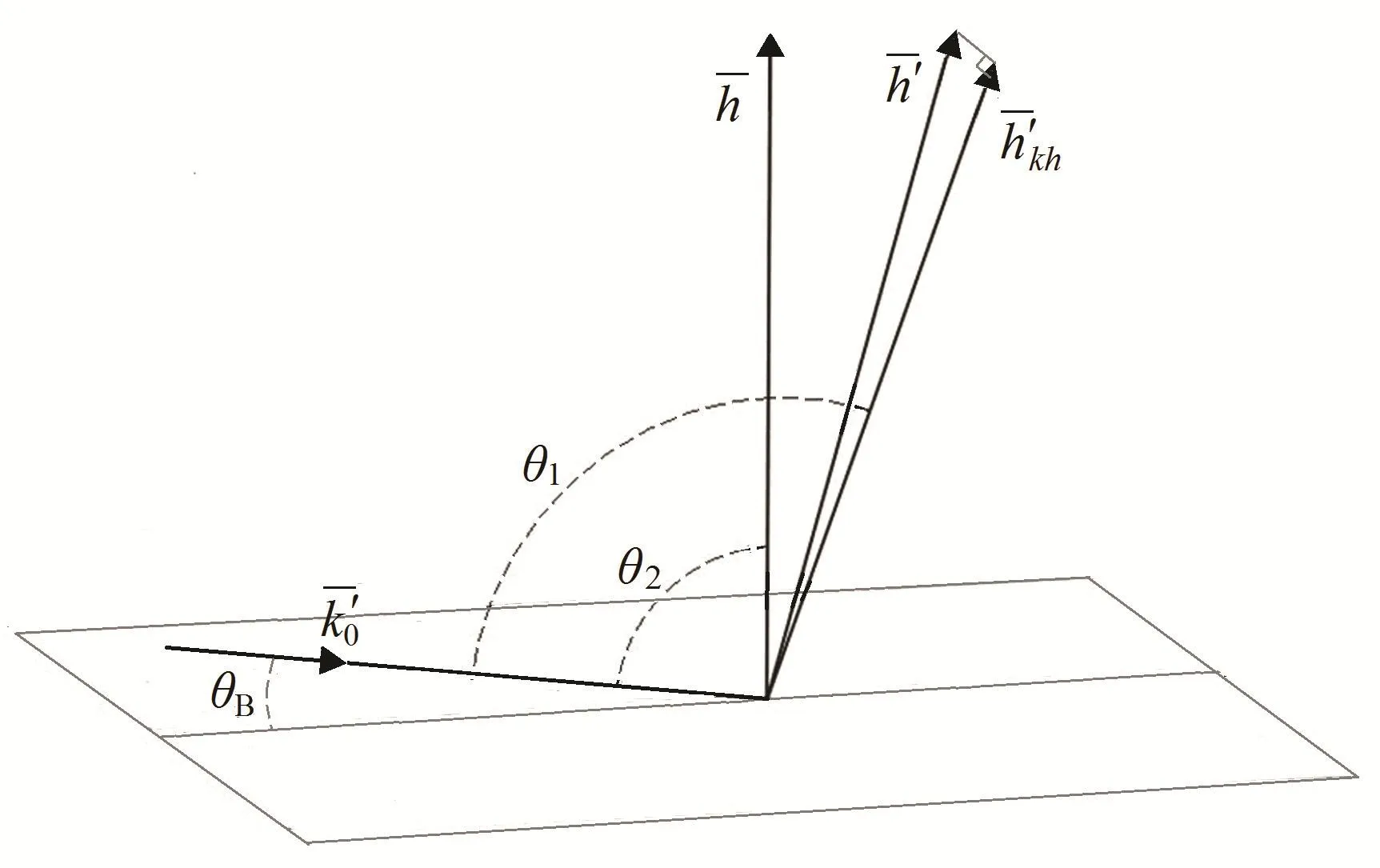
图1 θ1、θ2示意图Fig.1 Sketch map of θ1、θ2.
采用ANSYS[2]软件进行数值模拟,得出晶体在外加条件下的变形量,即每个单元里各节点的位移(UX,UY,UZ),即式(2)中的(u, v, w)。在ANSYS中读出各节点的位置坐标(x, y, z)和位移(u, v, w)后,用MATLAB软件对式(2)–(4)编程算得所选单元所需节点的U(rint, sint, tint),然后对所需节点在各单元不同U(rint, sint, tint)值进行平均得出Uavg,代入式(1)求出变形后的倒格矢,再对公式(5)编程计算,即得变形晶体的Δω。
1.2 面形误差法[4]
面形误差法是采用变形晶体受光表面光斑中心线上垂直表面位移沿子午方向的倾斜误差(slope error)表征变形晶体Darwin宽度展宽的方法,通常用曲线倾斜误差的RMS值表征。
SE为晶体的表面倾斜误差,UD为晶面上各点在垂直晶体受光表面方向上的位移,Y为晶面子午方向上各点的坐标位置。
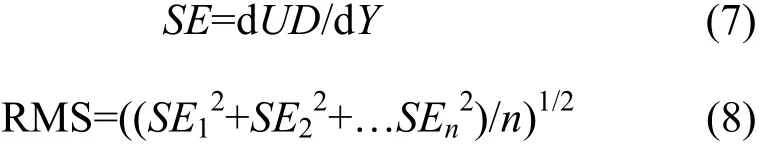
其中n为取点的个数。
2 数值模拟结果
2.1 完整晶体Darwin宽度的计算
根据晶体中X射线衍射原理[5]及文献[6]的理论计算,完整晶体Si(111)在波长1.54时的反射率曲线如图2,P=1(即π偏振),对称(b=1)Bragg本征反射,算得晶体本征Darwin宽度为36.67 μrad。
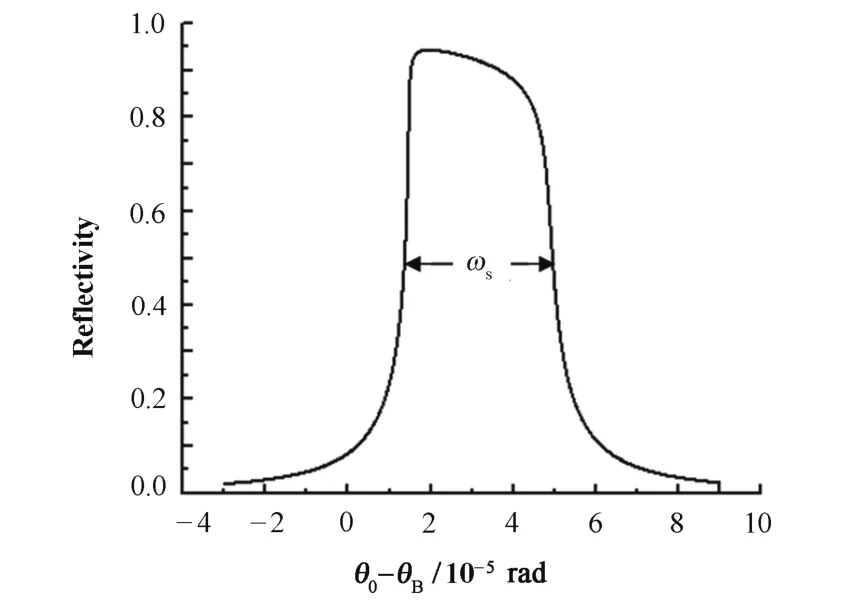
图2 完整晶体的反射曲线Fig.2 The reflectivity curve of undistorted crystal.
2.2 机械压弯变形晶体
图3为模拟的Si(111)晶体压弯结构示意图,晶体长140 mm,宽60 mm,高40 mm。运用ANSYS软件模拟计算,压弯半径R=610 m,1 mm网格,杨氏模量169 GPa,泊松比0.3。
用倒格矢法从ANSYS结果中读出各单元节点的位置(X, Y, Z)、位移(UX,UY,UZ)值,由 MATLAB程序计算可得压弯后晶体的Δω为11.06 μrad。
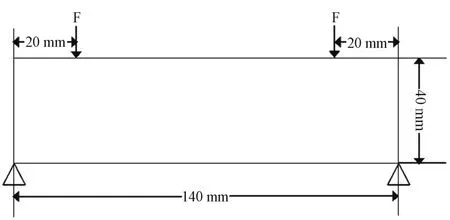
图3 晶体压弯结构示意图Fig.3 Figure of bend crystal.
图4是用面形误差法给出的模拟结果,光斑中心线上垂直方向的最大变形量为0.0128 mm,光斑中心线的倾斜误差为33.88 μrad,RMS=10.01 μrad。
2.3 弧矢聚焦晶体单色器直接水冷晶体
本文对上海光源BL16光束线弧矢聚焦晶体单色器直接水冷第一晶体进行数值模拟。Si(111)晶面承受储存环200 mA产生的热负载,晶体热导率148 w·m–1ºC,杨氏模量130 GPa,泊松比0.3,热膨胀系数2.2×10–6ºC–1。晶体中水槽内水压和Si-Cu接触面的压力均为0.2 MPa[7]。
采用ANSYS软件进行稳态热分析,再进行热-结构的顺序耦合计算,模拟直接水冷却晶体纯热负载引起的热变形。倒格矢法和 RMS值法模拟结果分别为4.12 μrad和3.89 μrad。
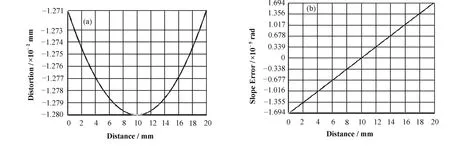
图4 ANSYS结果 (a) 光斑中心线的位移,(b) 光斑中心线的斜率误差Fig.4 Result from ANSYS.(a) Displacement of center line on the footprint, (b) Slope error of center line on the footprint
图5是200 mA热负载下的模拟结果,光斑中心线上垂直方向的最大变形量为 0.73 μm,光斑中心线的倾斜误差峰谷值为 12.05 μrad,RMS 3.89 μrad。
3 讨论
采用倒格矢法对晶体 Si(111)(简单压弯变形晶体和弧矢聚焦晶体单色器直接水冷却晶体)进行数值模拟计算,结果与实验值误差约17%,吻合程度有待提高。
分析其原因可能是数值模拟中未考虑弧矢方向晶体变形的影响,但实验测试结果中包含晶体弧矢方向变形和晶体Bragg角调节过程中弧矢方向耦合的贡献,造成出射光在弧矢方向的偏转。对光斑中心弧矢方向1 mm范围内变形对入射角变化的影响按子午方向同样方法进行模拟,得入射角变化3.36 μrad。用均方根法综合考虑弧矢和子午方向的影响,则Darwin宽度展宽保守值为5.32 μrad。因此变形晶体Darwin宽度展宽实际值应为4.12–5.32 μrad,覆盖了5.0 μrad实验值。
本文推荐采用的倒格矢数值模拟方法计算结果比 RMS值方法更接近实验结果,在预测晶体分光性能具有一定的优越性,对改进直接水冷却单色器的摇摆曲线模拟计算过程及同步辐射光束线晶体单色器的设计加工有指导意义。
1 Oversluizen T. Performance of a directly water-cooled silicon crystal for use in high-power synchrotron radiation applications[J]. Rev Sci Instum, 1989, 60(7): 1493–1500
2 Release 12.0 documentation for ANSYS: swanson analysis system Inc, Champain[Z]. Illinois, USA, 2009
3 ZHANG L, Lee W K, Michael W, et al. The performance of a cryogenically cooled monochromator for an invacuum undulator beamline[J]. J Synchrotron Rad, 2003, 10, Part.4: 313–319
4 Zachariasen W H. Theory of X-ray diffraction in crystals ch III[M]. New York: Dover Publication, INC.1945
5 Kikuta S. X-Ray crystal collimators using successive asymmetric diffractions and their applications to measurements of diffraction curves II type I collimator[J]. J Phys Soc, 1971, 30, 222–227
6 WANG Naxiu, LIU Shilei, XU Zhongmin, et al. Cooling of double crystal monochromator with sagittal focus at SSRF[J]. Nucl Sci Tech, 2010, 21(2): 65–68
7 王 劼. 上海光源BL16B测试报告[R]. 上海: 上海应用物理研究所, 2009
WANG Ji. SSRF test report of BL16B[R]. Shanghai: Shanghai Institute of Applied Physics, 2009
